不知道是因为这样的套路太典了还是因为什么，这难度只有绿题，可是我感觉好难想到QwQ

不过今天写了好几道倍增，好像有点感觉了捏

P1613 跑路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意：

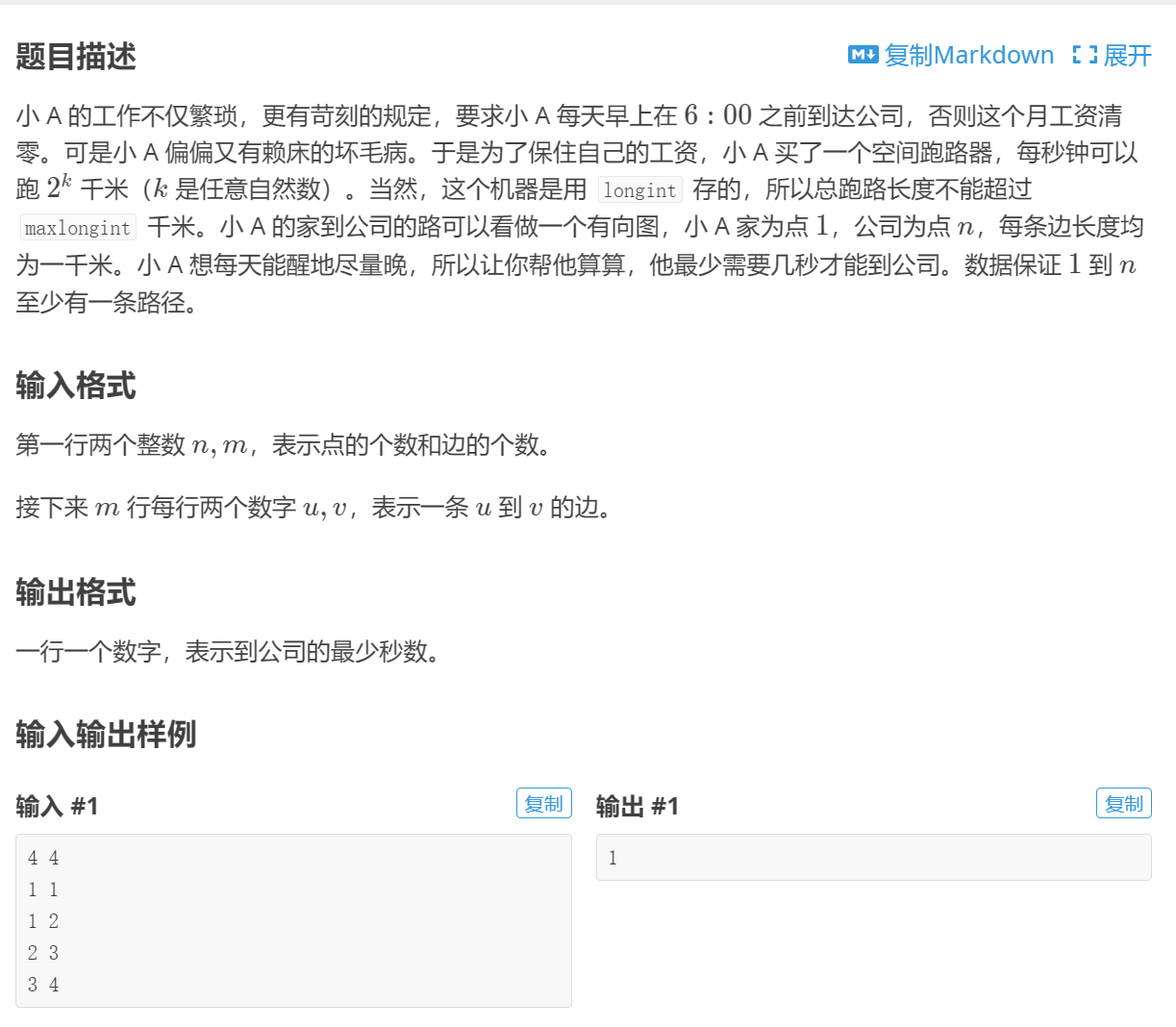
思路：

一开始的思路就是建图然后跑最短路

但是怎么建图呢

注意到：当两个结点直接的距离位表示中只有一个1，边权就是1

因此去看哪些点之间的距离位表示中只有一个1

然后就不会了

事实上建图部分应该由倍增去完成

具体地说，我们用DP去解释倍增可能比较好解释

设G[i][j][z]=1表示结点i和结点j之间的距离的位表示中第z位为1

这样的话，我们以二进制位作为阶段去DP

枚举另外一个点k，如果结点i和结点k的距离和结点j和结点k的距离的第z-1位都为1，那么两个距离相加一定会进位，即i和j之间的距离的第z位一定为1

感觉很神秘啊，我看完题解理解了好一会呜呜

感觉这可能就是倍增和图论的应用之一吧，用倍增来预处理结点之间距离的位表示关系

然后就能建图了，跑个最短路就行了，最好用floyd，因为数据很小很小

Code：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mxn=60,mxe=1e4+10;
struct ty{
    int to,next;
}edge[mxe<<1];
int n,m,u,v;
int G[mxn][mxn][66],dis[mxn][mxn];
void init(){
    for(int z=1;z<=64;z++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                for(int k=1;k<=n;k++){
                    if(G[i][j][z-1]&&G[j][k][z-1]){
                        G[i][k][z]=1;
                        dis[i][k]=1;
                    }
                }
            }
        }
    }
}
void floyd(){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
            }
        }
    }
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++) dis[i][j]=1e18;
    }
    memset(G,0,sizeof(G));
    for(int i=1;i<=m;i++){
        cin>>u>>v;
        G[u][v][0]=1;
        dis[u][v]=1;
    }
    init();
    floyd();
    cout<<dis[1][n]<<'\n';
}

总结：

感觉倍增就是一种特殊的DP，以第几位作为阶段，转移的时候从k-1位转移过来，通常用于统计贡献从k-1位转移过来的那种计数DP，不懂，随便说的，具体怎么样可能还得再做几题感受一下

然后和图论的结合的话，感觉应该就是像这道题一样，倍增处理结点之间的位表示关系