本期介绍🍖
主要介绍：青蛙跳台阶问题，青蛙跳台阶与斐波那契数列的关系👀。

---

---

1. 题目

  从前有一只青蛙他想跳台阶，有n级台阶，青蛙一次可以跳1级台阶，也可以跳2级台阶；问：该青蛙跳到第n级台阶一共有多少种跳法。

---

2. 递归解题思路

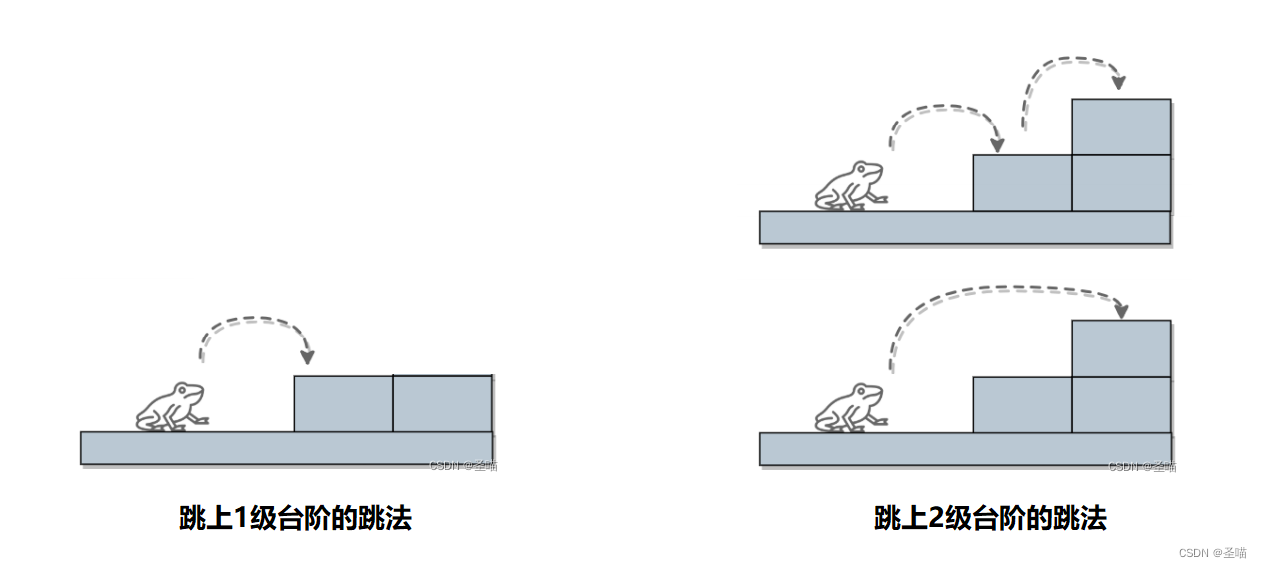
  当这只青蛙跳上了第n级台阶，它只可能是从(n-2)级或(n-1)级台阶跳上第n级台阶的，因为这只青蛙每次要么跳1级台阶，要么2级台阶。假设通过跳上第(n-2)级台阶有StepJump(n-2)种跳法，第(n-1)级台阶有StepJump(n-1)种跳法。那么青蛙从第(n-2)级台阶跳上第n级台阶就有StepJump(n-2)种跳法，同理青蛙从第(n-1)级台阶跳上第n级台阶就有StepJump(n-1)种跳法，那么必然可以得到：StepJump(n) = StepJump(n-1) + StepJump(n-2)，如下图所示：

  照这样演化下去，跳上某级台阶的跳法等于前两级台阶跳法的和。如此往下递推，直到计算跳上第1级台阶和第2级台阶的跳法，如下图所示。青蛙跳上1级台阶只有一种跳法，跳上2级台阶有2种跳法，以此作为递归函数的限制条件。

  代码如下：

#include<stdio.h>

int StepJump(int n)
{
	if (n == 1)
	{
		return 1;
	}
	else if (n == 2)
	{
		return 2;
	}
	else
	{
		return StepJump(n - 1) + StepJump(n - 2);
	}
}

int main()
{
	int n = 0;//需要跳的台阶数
	while (scanf("%d", &n) == 1)
	{
		int back = StepJump(n);
		printf("跳上第%d级台阶有>：%d种跳法\n", n, back);
	}
	return 0;
}

---

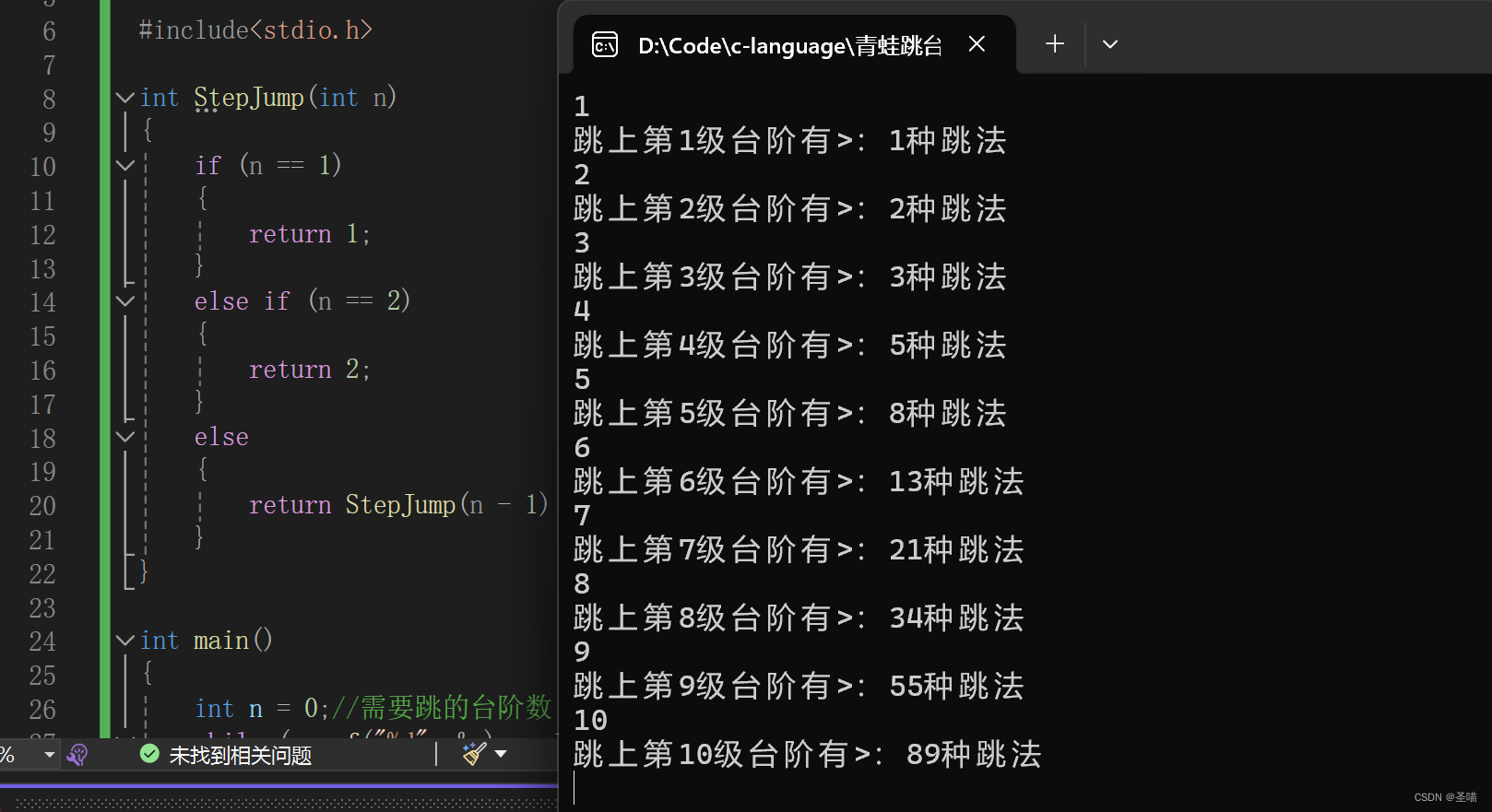
3. 迭代解题思路

  青蛙跳台阶特点：跳上某级台阶的跳法等于前两级台阶跳法的和，斐波那契数列的特点：每一项等于前两项之和。大家会惊讶的发现，青蛙跳平台问题的本质就是斐波那契额数列的运算。
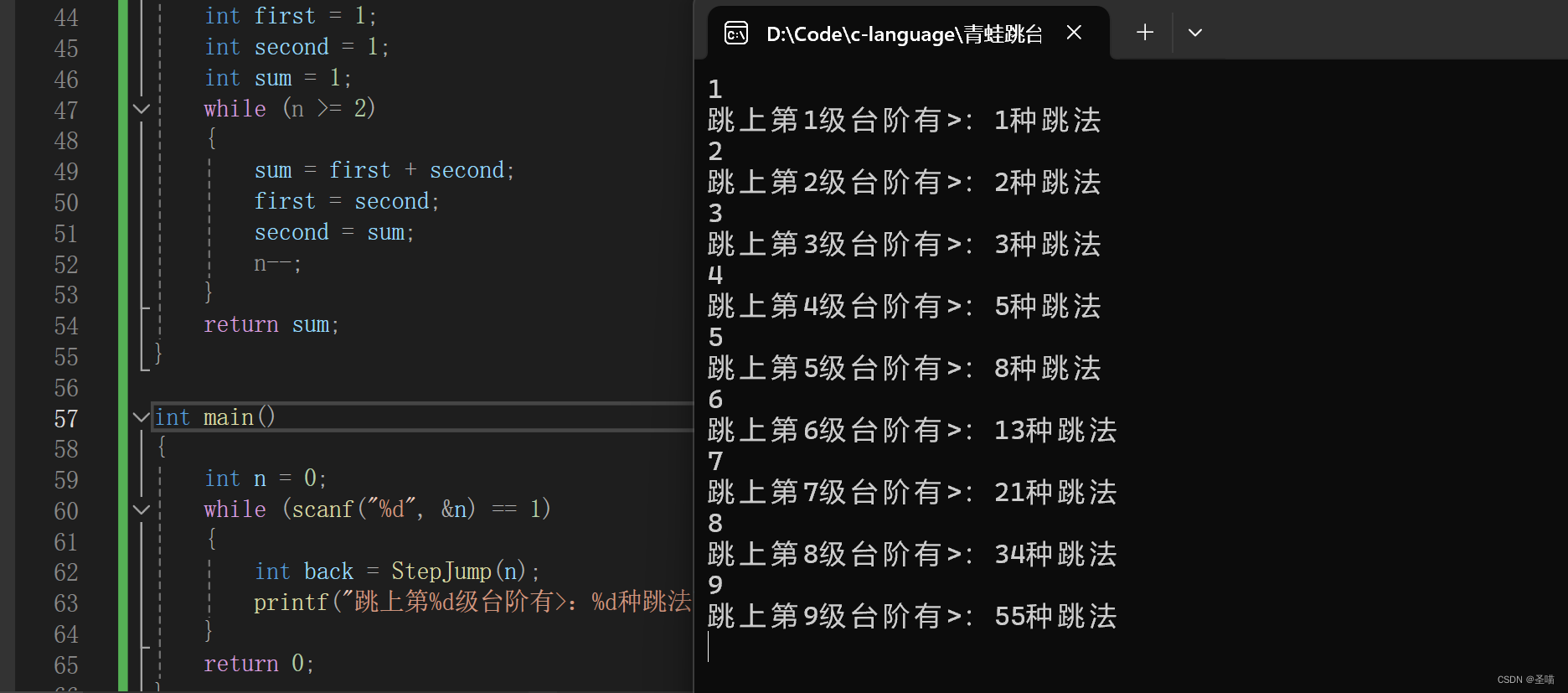
  通过求斐波那契数那一章学习，会得知使用递归实现求斐波那契数，会导致过多的冗余计算，效率过于低下。所以不妨使用迭代的思路来解决青蛙跳台阶问题，跳上1级台阶有1种跳法，跳上两级台阶有3种跳法。从第3级台阶开始往后，每级台阶都是前两级台阶跳法的和。实现代码如下：

#include<stdio.h>

int StepJump(int n)
{
	int first = 1;
	int second = 1;
	int sum = 1;
	while (n >= 2)
	{
		sum = first + second;
		first = second;
		second = sum;
		n--;
	}
	return sum;
}

int main()
{
	int n = 0;
	while (scanf("%d", &n) == 1)
	{
		int back = StepJump(n);
		printf("跳上第%d级台阶有>：%d种跳法\n", n, back);
	}
	return 0;
}

---

这份博客👍如果对你有帮助，给博主一个免费的点赞以示鼓励欢迎各位🔎点赞👍评论收藏⭐️，谢谢！！！
如果有什么疑问或不同的见解，欢迎评论区留言欧👀。