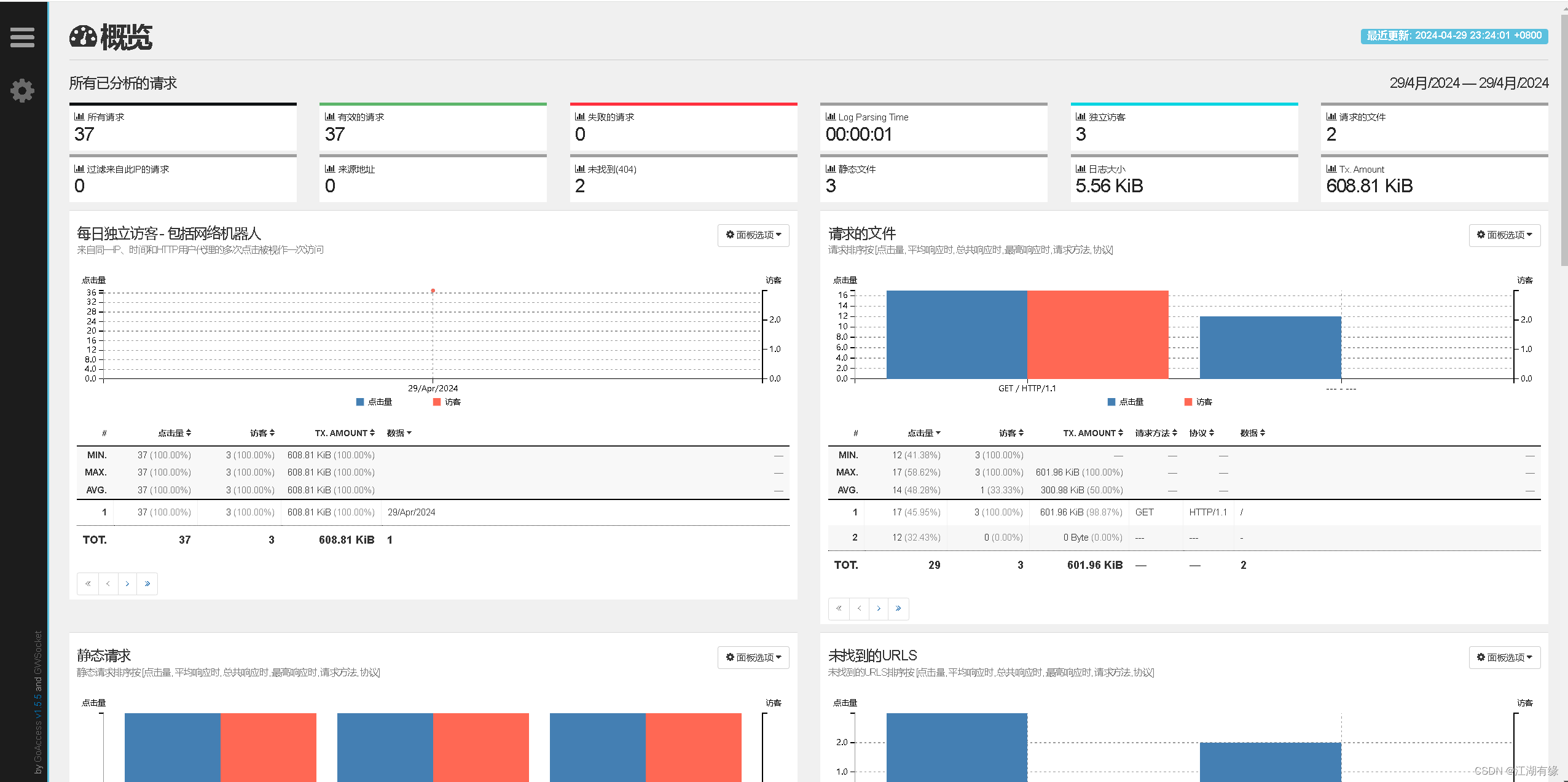
重点：
1. 群及子群的定义及相关结论
2. 群的判断,子群的判断
3. 群的阶,元素的阶,它们的相互关系
4. 同态,同构,核子群

2.1群的定义

定义：设G是一非空集合。如果在G上定义了一个代数运算，称为乘法，记为ab，而且这个运算满足下列条件，那么G称为一个群：
1) G对于乘法是封闭，即对于G中任意元素a，b，有ab∈G；（封闭性）
2) 对于G中任意元素a，b，c，有(ab)c = a(bc) ；（交换律）
3) 在G中有一个元素e，对于G中任意元素a，有 ea=a；（左单位元）
4) 对于G中任一元素a都存在G中的一个元素b，使ba=e。（左逆元）

整数对于加法构成了整数加法群。
全体整数Z，全体实数R，全体复数C对于加法构成群(Z，+),(R，+),(C，+)；
全体非零实数R*=R\{0}对于乘法是群(R*, · )；
同样非零有理数，非零复数对乘法也构成了群，分别记作 (Q*，·),(C*，·)，这类群称为数群。

例：自然数集合 N＝{1，2，3，...} 对于通常的加法(1) 封闭且满足结合律，(2) 不存在单位元和逆元，因此对于加法不是群。

例：集合{0，1}对于模2加法“⊕”（或称异或）是一个群。 (1) 封闭性和结合律满足；(2) 单位元e=0，因为 0⊕0＝0，0⊕1＝1； (3) 每一个元素的逆元就是它自己：0⊕0=0，1⊕1=0。  {0，1}对于⊕运算是加法群。

例：集合的元素不一定是数，集合元素为二阶方阵的例子：

该集合对于矩阵的普通乘法是一个群，逆 元是其元素本身，单位元是

例：考虑二阶矩阵集合，其中a，b，c，d为整数， 

则该集合对于普通矩阵乘法构成群：
1)封闭性：两个矩阵A和B相乘仍然是整数二阶矩阵，而且|AB|＝|A||B|=1；

2) 结合律显然满足；

3) 单位矩阵是单位元；

4) 任意元素的左逆元为。

定义：如果群中的运算满足交换律，则这个群称为交换群或阿贝尔(Abel)群。比如: (Z，+)，(R，+)，(C，+) 都是Abel群。
注：集合元素可以是任意事物，其中的运算也可以是任意定义的。

群的基本性质：
1) 左逆元同时也是右逆元，即对于a，b∈G，如果ba=e，则ab = e；
2) 左单位元同时也是右单位元，即如果对于所有a∈G有ea = a，则对于所有a∈G也有ae = a；
3) 单位元是唯一的；
4) 逆元是唯一的。

定义：如果一个群G中元素的个数是无限多个，则称G是无限群；如果G中的元素个数是有限多个，则称G是有限群，G中元素的个数称为群的阶，记为|G|。

由于群里结合律是满足的，所以元素连乘a1a2…an有意义，它也是G中的一个元。
把a的n次连乘记为a^n， 称为a的n次幂，即。

还将a的逆元a^(-1)的n次幂记为a^(-n)，即。
群的逆元=a。

群的阶、元素的幂

群的等价性质：
定理：一个群的乘法满足消去律：如果ax=ax’，则x=x’；（左消去） 如果ya=y’a，则y=y’。 （右消去）

定理：如果G是一个群， ∀a,b∈G，方程 ax=b，ya=b有解; 反之，如果上述方程在非空集合G中有 解，而且其中的运算封闭且满足结合律，则G是一个群。

定理：如果一个非空有限集合G中的运算封闭且满足结合律，则它是一个群的充分必要条件是满足消去律。

2.2子群

定义：一个群G的一个子集H如果对于G的乘法构成一个群， 则称H为G的子群，记作H≤G。 一个群G至少有两个子群：G本身；只包含单位元的子集{e}， 它们称为G的平凡子群，其他子群成为真子群(H<G)。

例：设m是一个正整数。整数加群Z中每个元素的m倍数 {0，±m，±2m，±3m，…} 对加法也构成群，它是Z的子群，记为mZ。

引理：一个群G和它的一个子群H有：1) G的单位元和H的单位元是同一的；2) 如果a∈H，a^(-1)是a在G中的逆元，则a^(-1)∈H。

子群的判定定理
定理：一个群G的一个非空子集H构成一个子群的充分必要条件是：
1) ∀a,b∈H，有ab∈H；（运算封闭）
2) ∀a∈H，有a^(-1)∈H。（逆元存在）
★定理：一个群G的一个非空子集H构成一个子群的充分必要条件是：对于∀a,b∈H，有：ab^(-1)∈H。
定理：一个群G的一个非空有限子集H构成一个子群的充分必要条件是：对于任意a，b∈H，有ab∈H。

例：判断mZ是Z的加法子群。

2.3同构与同态

定义：一个集合A到另一个集合B的映射f是∀a∈A， 都有一个确定的 b = f(a)∈B 与之对应。b称为a在f下的像，a称为b在f下的一个原像。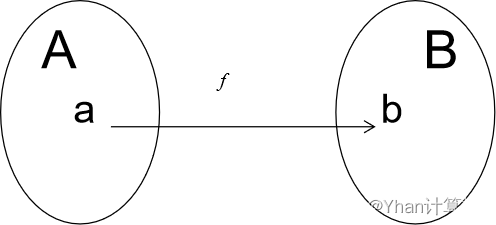

映射
单射：∀a, b∈A，如果a≠b，则 f(a)≠f(b)。
满射：∀b∈B，总有a∈A，使f(a)=b。
一一映射：既是满射又是单射的映射。

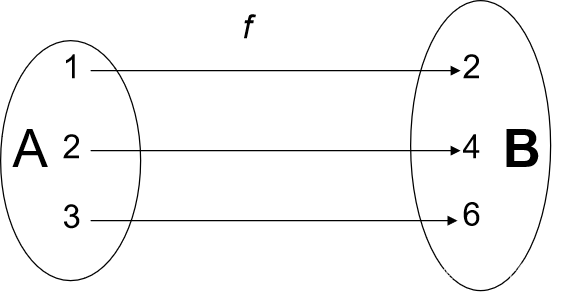
例：设A={1，2，3}，B={2，4，6}。 下图中的映射f是一个单射，又是一个满射，它是一一映射。

一一映射 f :A→B 存在一个逆映射 f^(-1)：B→A，它也是一一映射。

如果A=B，映射f也称为变换，即一个集合到自身的映射称为变换。如果一个集合A到自身的映射f定义为：对于任意a∈A， f(a)=a， 则称映射f为恒等映射，单位映射或恒等变换，记为I。

定义：假设G和G’是两个群，若存在映射f：G→G’ 满足：∀a, b∈G，均有 f(a·b)= f(a)⊙f(b)则称f是G到G’的一个同态映射或简称同态。
如果f是单射，则称f是单同态；
如果f是满射，则称f是满同态；
如果f是一一映射，则称f是同构映射；
如果G=G’，同态f称为自同态，同构映射f称为自同构映射。

例：设整数集合Z里的运算是加法，Z通过映射 f:a→e^a 产生一个非零实数集合{ea|a∈Z}。我们定义这个实数集合里的运算是乘法，于是有 f(a+b)=f(a)f(b)， 显然Z中的运算在{ea|a∈Z}中得到了保持，f就是一个同态映射。

若同态映射还是一一映射，则称为同构映射。

例：映射f：a→e^a就是一个一一映射，所以f为同构映射。

定理：设G和G’是两个群，在G到G’的一个同态映射f之下， 
1) G的单位元e的像f(e)是G’的单位元e’，即 f(e) = e’；
2) G的任意元a的逆元a^(-1)的像f(a^(-1))是f(a)的逆元，即 f(a^(-1)) = f(a)^(-1)；
3) G在f下的像的集合{f(a)|a∈G}是G’的子群，称为f的像子群。当f是满同态时，像子群就是G’本身。

定义：设G和G’是两个群，如果存在一个G到G’的同构映射，则称G与G’同构，记为G≌G’。如果G=G’，则称G自同构。
整数加法群Z和偶数加法群E同构。
实数加法群R和正实数乘法群R+同构。同构映射为f(a) = ea。

例：任意一个二阶群都与乘法群{1，-1}同构。
证明：设一个任意二阶群为A={e，a}，e为单位元。
构造A到乘法群{1，-1}的映射： f：e→1，a→-1。

则f是同构映射，故A与乘法群{1，-1}同构。

群的同构具有反身性，对称性和传递性，即它是等价关系：
1) G≌G；
2) 由G≌G’可推出G’≌G；
3) 由G≌G’和G’≌G’’可推出G≌G’’。

定义：设f是G到G’的同态映射。∀a’∈G’，集合 {a|f(a)=a’, a∈G}可能是空集，也可能包含一个以上 的元素(f不是单射)。这个集合称为a’的完全反像。
特别地，单位元的完全反像称为同态映射f的核，记为ker(f)，即ker(f) = {a|a∈G,f(a)=e’}

定理：ker(f)是G的子群，称为f的核子群。
证明：
由于e∈ker(f)，所以ker(f)不会是空集。
如果 a, b∈ker(f)，则 f(a)=e’，f(b) = e’，f(b)^(-1) = (e’)^(-1)=e’，
于是 f(ab^(-1)) = f(a)f(b^(-1)) = f(a)f(b)^(-1) = e’e’ = e’，
所以ab^(-1)∈ker(f)，故ker(f)是G的子群。 

定理：G到G’的同态映射f是单同态的充要条件是ker(f)={e}，即核子群只含有单位元。
证明：
充分条件。反证法。如果存在a，b∈G，a∈b，有 f(a)=f(b)，
于是f(a)f(b)^(-1)=e’，由于f是同态，则 f(ab^(-1)) = e’。
而由a≠b，有ab^(-1)≠e，这与ker(f)={e}矛盾，故f是单射，因而是单同态。
必要条件：由于e∈ker(f)，如果ker(f)还包含其他元素，则f不是单射，故 ker(f) = {e}。

同态映射和核子群、像子群的关系：