Markov Transition Field(马尔科夫转移场,简称MTF)是一个用来表示时间序列数据中不同时间点之间状态转移概率的可视化工具。简单来说,它展示了一个时间点上的状态如何可能转移到另一个时间点的状态,这些转移概率是通过统计数据得出的。通过这种方式,MTF能帮助我们直观地理解时间序列数据中状态的变化规律和趋势。
1. 代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
def discretize_signal(signal, n_bins):
"""离散化信号"""
bins = np.linspace(np.min(signal), np.max(signal), n_bins)
digitized = np.digitize(signal, bins) - 1 # 返回每个值所属的区间
return digitized
def compute_transition_matrix(digitized_signal, n_states):
"""计算转移矩阵"""
matrix = np.zeros((n_states, n_states))
for (i, j) in zip(digitized_signal[:-1], digitized_signal[1:]):
matrix[i, j] += 1
# Normalize each row to sum to 1
matrix = np.divide(matrix, np.maximum(np.sum(matrix, axis=1, keepdims=True), 1))
return matrix
def create_markov_transition_field(matrix, digitized_signal):
"""根据转移矩阵和离散信号创建MTF"""
signal_length = len(digitized_signal)
mtf = np.zeros((signal_length, signal_length))
for i in range(signal_length):
for j in range(signal_length):
mtf[i, j] = matrix[digitized_signal[i], digitized_signal[j]]
return mtf
# 示例数据生成
np.random.seed(0)
time_series = np.random.rand(100) * 100 # 生成100个数据点
# 离散化和计算MTF
n_states = 10 # 状态数
digitized_signal = discretize_signal(time_series, n_states)
transition_matrix = compute_transition_matrix(digitized_signal, n_states)
mtf = create_markov_transition_field(transition_matrix, digitized_signal)
# 应用高斯模糊
mtf_blurred = gaussian_filter(mtf, sigma=1.0)
# 绘制结果
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.title('Original MTF')
plt.imshow(mtf, cmap='hot', origin='lower')
plt.colorbar()
plt.subplot(122)
plt.title('Blurred MTF')
plt.imshow(mtf_blurred, cmap='hot', origin='lower')
plt.colorbar()
plt.show()
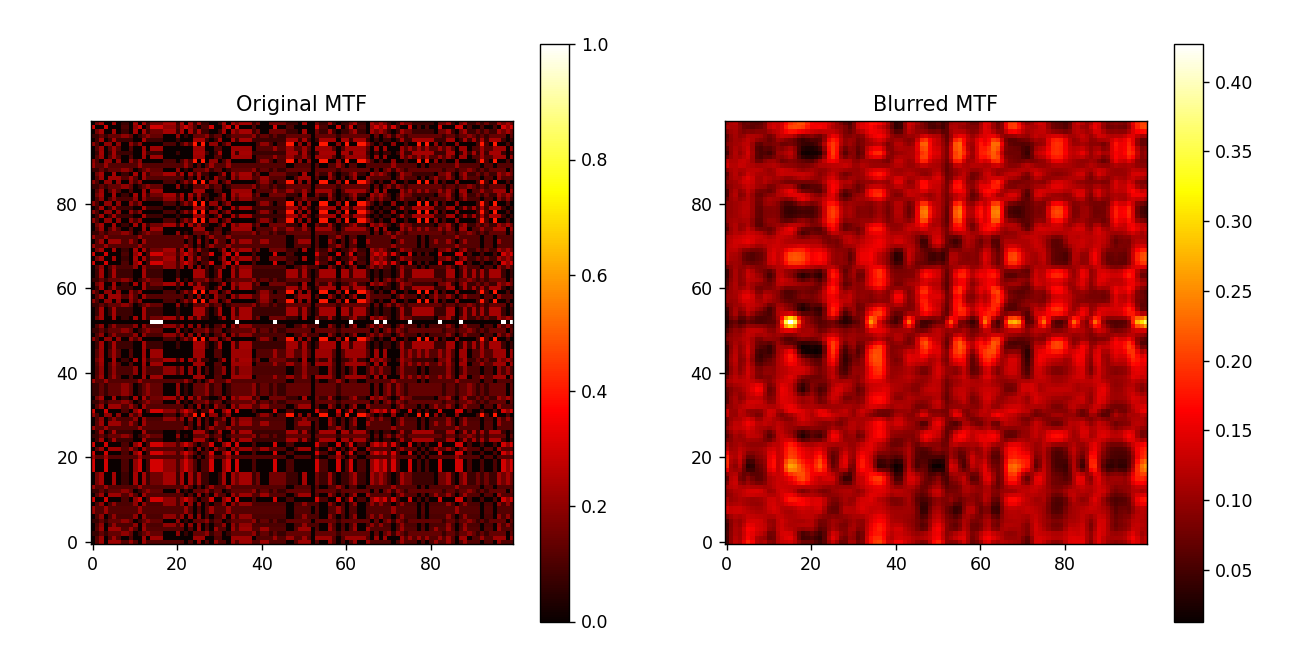
结果:
代码解释
整体解释:
这段代码的主要目的是从一个时间序列数据中生成一个Markov Transition Field (MTF),并对其进行高斯模糊处理,最后可视化原始和模糊后的MTF。首先,通过discretize_signal函数将连续的时间序列数据离散化为有限的几个状态。然后,使用compute_transition_matrix函数计算这些离散状态之间的转移概率。接着,create_markov_transition_field函数利用这个转移矩阵和离散化的信号来创建一个MTF。最后,对MTF应用高斯模糊,并绘制出原始和模糊后的MTF图像。
逐行代码解释:
- 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
- 定义
discretize_signal函数
def discretize_signal(signal, n_bins):
定义了一个函数,用于将连续信号离散化为n_bins个区间。
bins = np.linspace(np.min(signal), np.max(signal), n_bins)
在信号的最小值和最大值之间均匀划分n_bins个区间。
digitized = np.digitize(signal, bins) - 1
使用numpy.digitize函数将信号中的每个值分配到对应的区间,并减1以调整索引从0开始。
- 定义
compute_transition_matrix函数
def compute_transition_matrix(digitized_signal, n_states):
定义一个函数,用于根据离散化的信号计算状态转移矩阵。
matrix = np.zeros((n_states, n_states))
初始化一个n_states x n_states的零矩阵。
for (i, j) in zip(digitized_signal[:-1], digitized_signal[1:]):
matrix[i, j] += 1
遍历离散化信号,统计状态之间的转移次数。
matrix = np.divide(matrix, np.maximum(np.sum(matrix, axis=1, keepdims=True), 1))
将转移矩阵的每一行归一化,使其和为1。
- 定义
create_markov_transition_field函数
def create_markov_transition_field(matrix, digitized_signal):
定义一个函数,根据转移矩阵和离散信号创建MTF。
signal_length = len(digitized_signal)
mtf = np.zeros((signal_length, signal_length))
初始化一个signal_length x signal_length的零矩阵。
for i in range(signal_length):
for j in range(signal_length):
mtf[i, j] = matrix[digitized_signal[i], digitized_signal[j]]
填充MTF矩阵,其中的元素表示从信号中的某个状态转移到另一个状态的概率。
- 示例数据生成与处理
np.random.seed(0)
time_series = np.random.rand(100) * 100
生成一个包含100个数据点的随机时间序列。
n_states = 10
digitized_signal = discretize_signal(time_series, n_states)
transition_matrix = compute_transition_matrix(digitized_signal, n_states)
mtf = create_markov_transition_field(transition_matrix, digitized_signal)
对时间序列进行离散化,计算转移矩阵,并创建MTF。
- 应用高斯模糊并绘制结果
mtf_blurred = gaussian_filter(mtf, sigma=1.0)
对MTF应用高斯模糊。
接下来的代码使用matplotlib库绘制原始和模糊后的MTF图像。
这段代码展示了如何从时间序列数据中提取Markov Transition Field (MTF),并通过高斯模糊对其进行平滑处理,最后可视化这两个MTF图像。