1. 最长递增子序列

我们来看一下我们的贪心策略体现在哪里???

我们来总结一下:

我们在考虑最长递增子序列的长度的时候,其实并不关心这个序列长什么样子,我们只是关心最后一个元素是谁。这样新来一个元素之后, 我们就可以判断是否可以拼接到它的后面。因此,我们可以创建一个数组,统计长度为 x 的递增子序列中,最后一个元素是谁。为了尽可能的让这个序列更长,我们仅需统计长度为x的所有递增序列中最后一个元素的「最小值」。此时我们来算一下时间复杂度,首先我们要遍历整个数组,其次我们还要遍历长度为x的序列,那么此时的复杂度是O(N2),统计的过程中发现,数组中的数呈现「递增」趋势,因此可以使用「二分」来查找插入位置。
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> ret;
ret.push_back(nums[0]);
for(int i = 1; i < nums.size(); i++)
{
if(nums[i] > ret.back())
{
ret.push_back(nums[i]);// 如果能接在最后⼀个元素后⾯,直接放
}
else
{
// 使用二分找到插入位置
int left = 0;
int right = ret.size() - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(ret[mid] < nums[i])
{
left = mid + 1;
}
else
{
right = mid;
}
}
ret[left] = nums[i];// 放在 left 位置上
}
}
return ret.size();
}
};2. 递增的三元子序列

我们会发现这道题目就是最递增子序列的简化版,因此我们可以使用贪心的思想,找到最长子序列然后判断长度是否大于3即可解决,但是实际上我们不需要使用二分算法,因为我们只需要求出长度为3的子序列,仅需两次比较就可以找到插入位置,同时不用一个数组存数据,仅需两个变量即可,此时的时间复杂度为O(N).

直接来上代码:
class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
int a = nums[0];
int b = INT_MAX;
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] > b) return true;
else if(nums[i] > a) b = nums[i];
else a = nums[i];
}
return false;
}
};3. 最长连续递增序列

这个题目比较简单,找到以某个位置为起点的最长连续递增序列之后(设这个序列的末尾为 j 位置),接下来直接以 j + 1 的位置为起点寻找下⼀个最长连续递增序列,我们没有必要从i + 1位置进行寻找,因为 i 位置找到的序列肯定是最长的!!!
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int ret = 0;
int i = 0;
while(i < nums.size())
{
int j = i + 1;
// 找到递增区间的末端
while(j < nums.size() && nums[j] > nums[j-1])
{
j++;
}
ret = max(ret,j - i);
// 直接在循环中更新下⼀个位置的起点
i = j; // 贪心
}
return ret;
}
};4. 买卖股票的最佳时机

首先我们看到这道题目,第一想到的肯定是暴力枚举,我们可以依次枚举两个位置,然后进行相减,最后保存相减出来的最大值即可,但是这样的复杂度就是O(N2)的,此时我们就可以进行优化,我们在枚举卖出价格时候,并不用将前面买入的股票的价格依次枚举,我们只需要找到其中的最小值即可,这一个点就体现出来贪心的策略,由于只能交易⼀次,所以对于某⼀个位置 i ,要想获得最大利润,仅需知道前⾯所有元素的最小值。然后在最小值的位置「买入」股票,在当前位置「卖出」股票即可。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int prevmin = INT_MAX;
int ret = 0; // 记录最终结果
for(int i = 0; i < prices.size(); i++)
{
// 先更新结果
ret = max(prices[i] - prevmin, ret);
// 再更新最小值
if(prices[i] < prevmin)
prevmin = prices[i];
}
return ret;
}
};5. 买卖股票的最佳时机Ⅱ

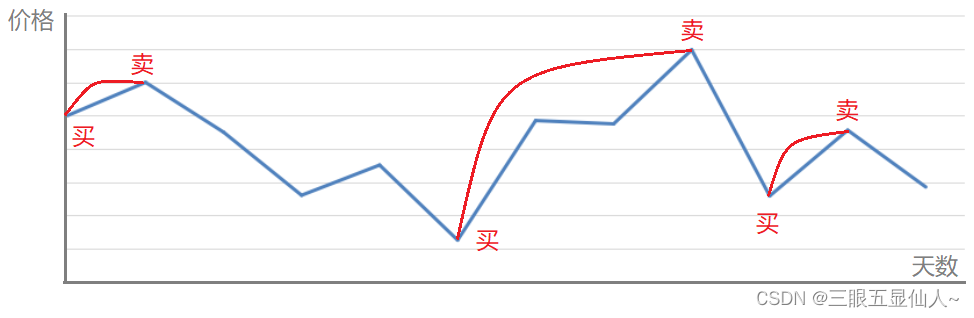
由于可以进行⽆限次交易,所以只要是⼀个「上升区域」,上升区间一定是稳赚的,我们就把利润拿到手就好了,这就是贪心策略。
⭐解法一:双指针
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ret = 0;
for(int i =0 ; i < prices.size(); )
{
int j = i;
while(j + 1 < prices.size() && prices[j + 1] > prices[j])
{
j++; // 寻找上升的区间
}
ret += prices[j] - prices[i];
i = j + 1;
}
return ret;
}
};⭐解法二:拆分交易,只要今天的股票的价格大于昨天,就可以累计到利润上
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ret = 0;
for(int i = 1; i < prices.size(); i++)
{
if(prices[i] > prices[i - 1])
ret += prices[i] - prices[i - 1];
}
return ret;
}
};