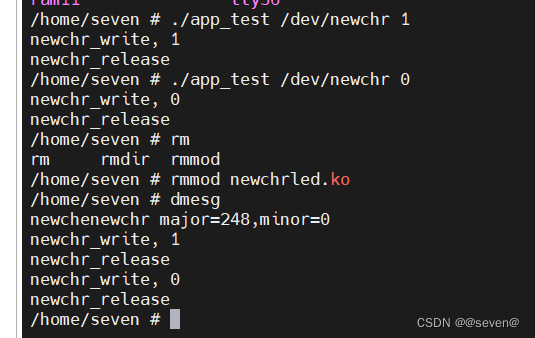
描述
Little Rosie has a phone with a desktop (or launcher, as it is also called). The desktop can consist of several screens. Each screen is represented as a grid of size 5×3, i.e., five rows and three columns.
There are x applications with an icon size of 1×1 cells; such an icon occupies only one cell of the screen. There are also y applications with an icon size of 2×2 cells; such an icon occupies a square of 4 cells on the screen. Each cell of each screen can be occupied by no more than one icon.
Rosie wants to place the application icons on the minimum number of screens. Help her find the minimum number of screens needed.
输入描述
The first line of the input contains t (1≤t≤104) — the number of test cases.
The first and only line of each test case contains two integers x and y (0≤x,y≤99) — the number of applications with a 1×1 icon and the number of applications with a 2×2 icon, respectively.
输出描述
For each test case, output the minimal number of required screens on a separate line.
用例输入 1
11 1 1 7 2 12 4 0 3 1 0 8 1 0 0 2 0 15 0 8 2 0 9
用例输出 1
1 1 2 2 1 1 0 1 1 2 5
提示
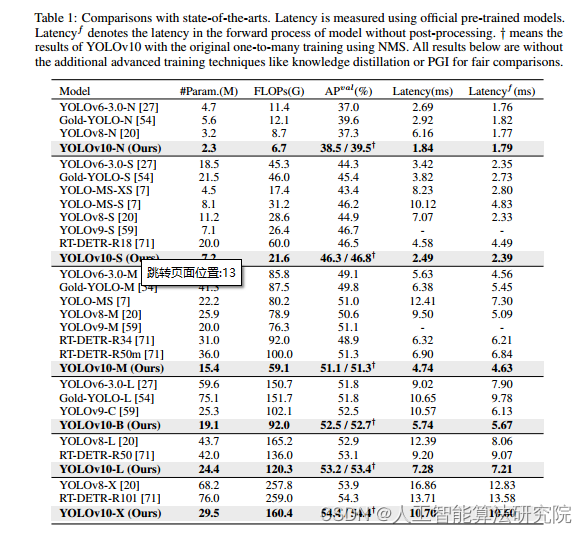
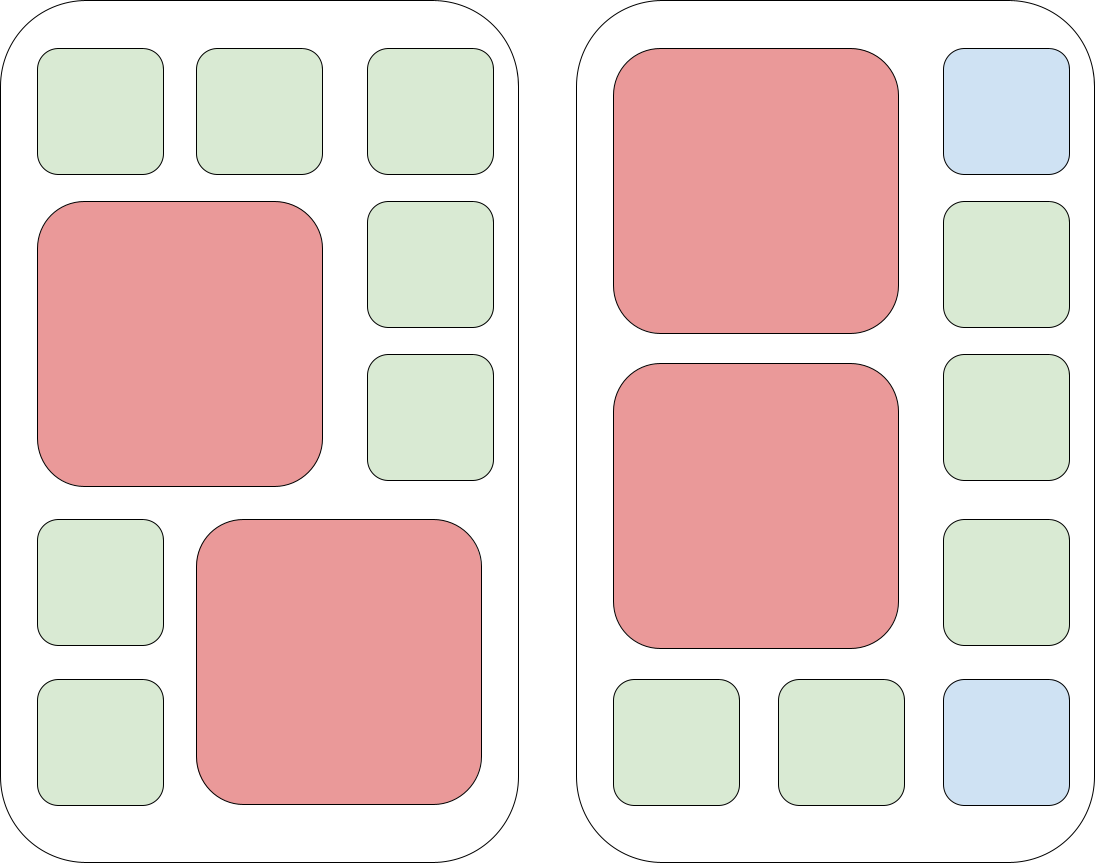
The solution for the first test case can look as follows:

Blue squares represent empty spaces for icons, green squares represent 1×1 icons, red squares represent 2×2 icons
The solution for the third test case can look as follows:
翻译:
描述
小罗茜有一部带桌面(或启动器,也称为启动器)的手机。桌面可以由多个屏幕组成。每个屏幕都表示为大小的网格5×3,即五行三列。
有x图标大小为1×1细胞;这样的图标只占据屏幕的一个单元格。还有和图标大小为2×2细胞;这样的图标占据了一个正方形4屏幕上的单元格。每个屏幕的每个单元格只能被一个图标占据。
Rosie 希望将应用程序图标放置在最少数量的屏幕上。帮助她找到所需的最小屏幕数量。
输入描述
输入的第一行包含t (1≤吨≤104) — 测试用例的数量。
每个测试用例的第一行也是唯一的一行包含两个整数x和和 (0≤ x,y≤99) — 具有1×1图标和带有2×2图标。
输出描述
对于每个测试用例,在单独的行上输出所需屏幕的最小数量。
用例输入 1
11
1 1
7 2
12 4
0 3
1 0
8 1
0 0
2 0
15 0
8 2
0 9
用例输出 1
1
1
2
2
1
1
0
1
1
2
5
提示
第一个测试用例的解决方案可以如下所示:

蓝色方块表示图标的空白区域,绿色方块表示1×1图标,红色方块代表2×2图标
第三个测试用例的解决方案如下所示:

解题思路:
先根据大的判断屏幕,一个屏幕最多俩大的,然后根据小的增加屏幕
c++代码如下:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
while(n--)
{
int small,big;
cin >> small >> big;
int res = 0;
res = big/2 + big%2;
if(small > 15*res - big*4)
{
small -= 15*res - big*4;
res += small/15 + (small%15 != 0);
}
cout << res << endl;
}
}