🔥 个人主页: 黑洞晓威
😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害
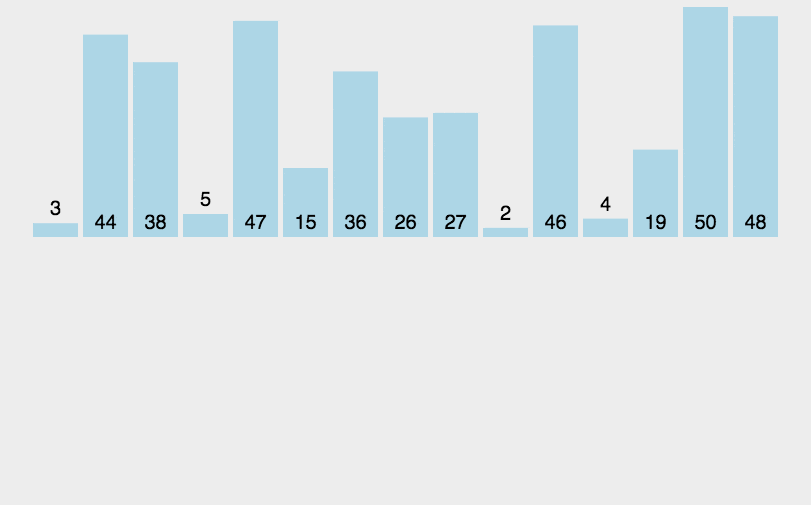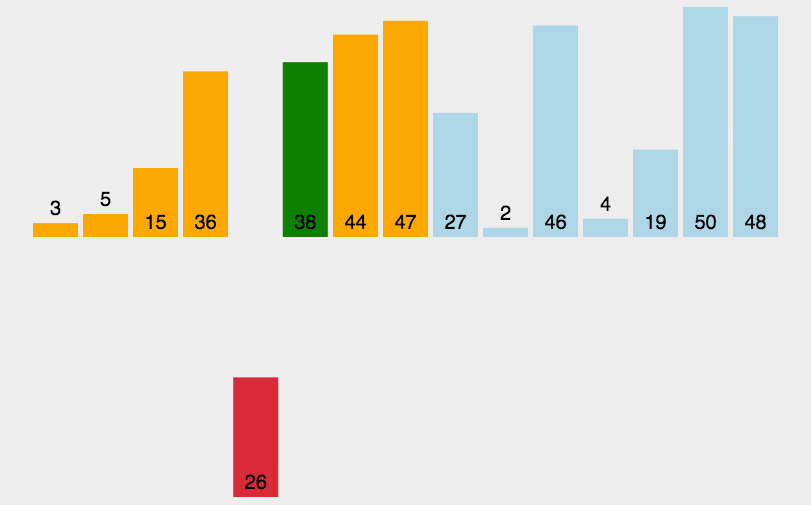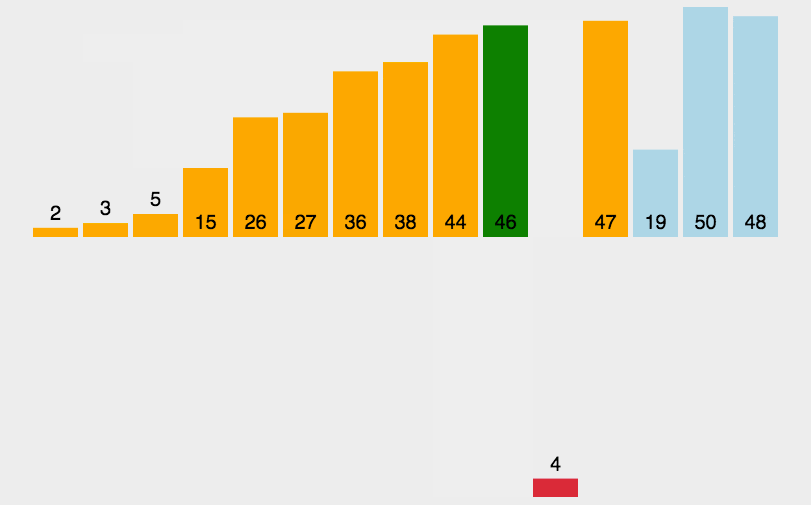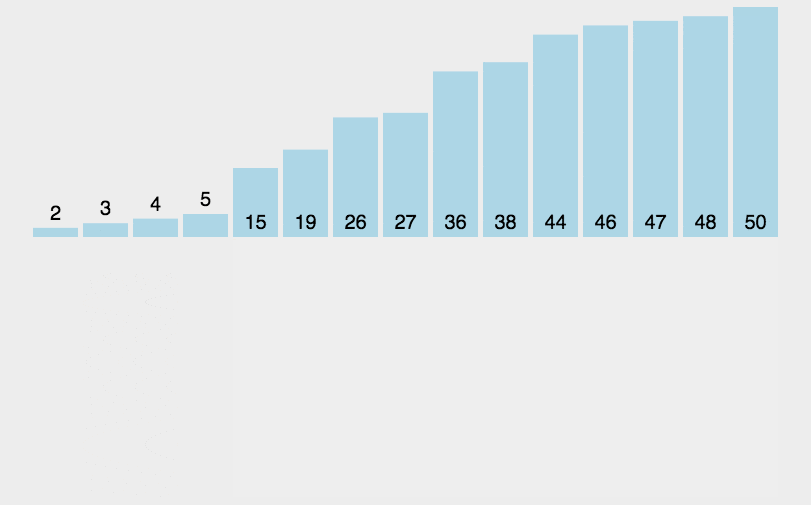
84. 柱状图中最大的矩形
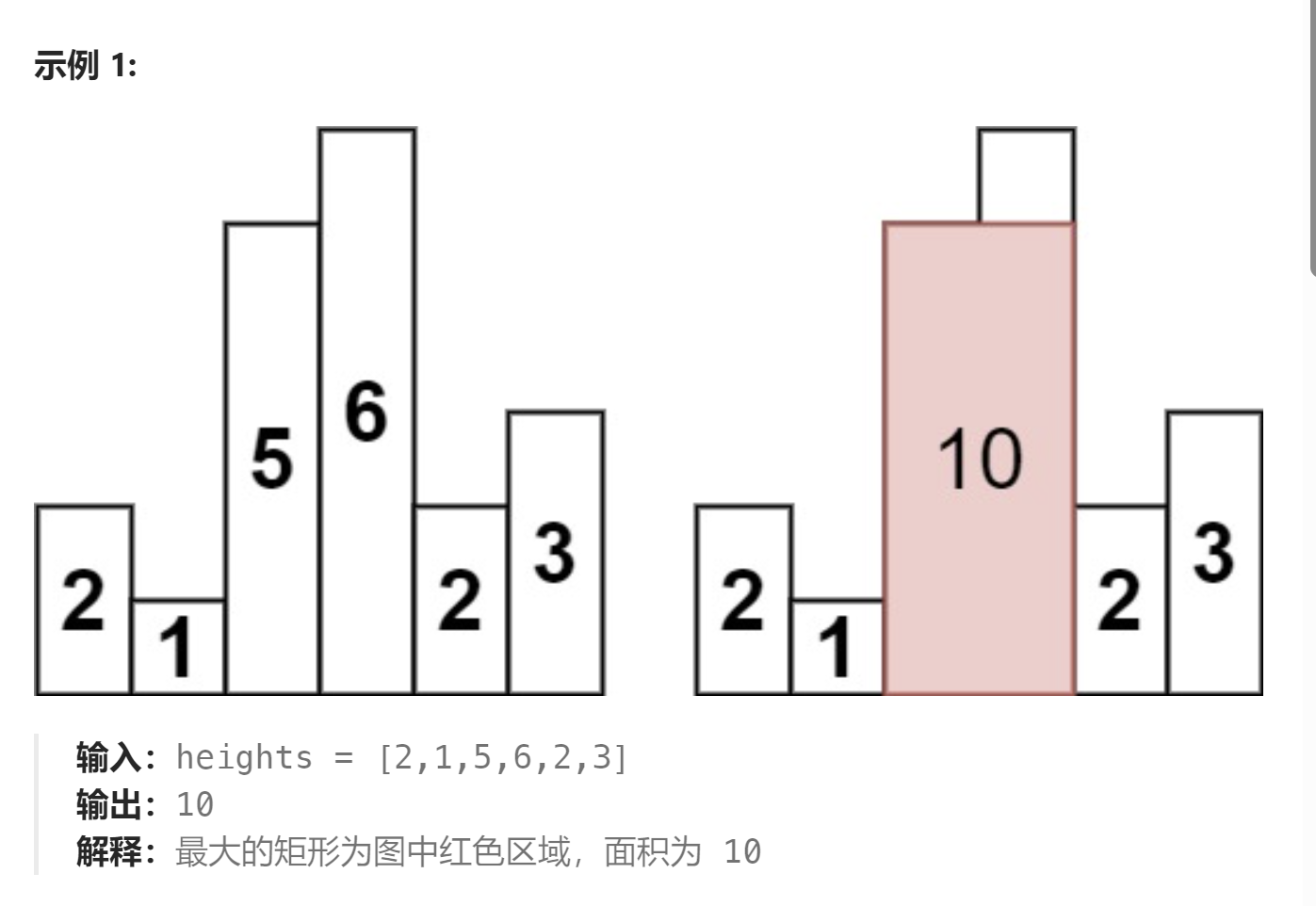
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
解题思路
要求在柱状图中勾勒出的最大矩形面积,可以使用单调栈来解决这个问题。基本思路如下:
- 维护一个栈,栈中存放柱子的索引。
- 遍历每根柱子,对于每根柱子,将其与栈顶元素比较:
- 如果当前柱子高度大于栈顶柱子高度,则将当前柱子的索引入栈。
- 如果当前柱子高度小于等于栈顶柱子高度,则不断出栈,计算以栈顶柱子为高度的矩形面积,并更新最大面积。
- 遍历完所有柱子后,对剩余栈中柱子依次计算面积,更新最大面积。
代码实现
import java.util.ArrayDeque;
import java.util.Deque;
class Solution {
public int largestRectangleArea(int[] heights) {
Deque<Integer> stack = new ArrayDeque<>();
int maxArea = 0;
for (int i = 0; i <= heights.length; i++) {
int h = (i == heights.length) ? 0 : heights[i];
if (stack.isEmpty() || h >= heights[stack.peek()]) {
stack.push(i);
} else {
while (!stack.isEmpty() && h < heights[stack.peek()]) {
int top = stack.pop();
int width = stack.isEmpty() ? i : i - 1 - stack.peek();
maxArea = Math.max(maxArea, heights[top] * width);
}
stack.push(i);
}
}
return maxArea;
}
}
295. 数据流的中位数
中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
- 例如
arr = [2,3,4]的中位数是3。 - 例如
arr = [2,3]的中位数是(2 + 3) / 2 = 2.5。
实现 MedianFinder 类:
MedianFinder()初始化MedianFinder对象。void addNum(int num)将数据流中的整数num添加到数据结构中。double findMedian()返回到目前为止所有元素的中位数。与实际答案相差10-5以内的答案将被接受。

实现思路:
- 使用一个最大堆存储数据流中较小的一半数字,一个最小堆存储数据流中较大的一半数字。
- 添加新元素的时候,首先将其插入最大堆,然后从最大堆中取出堆顶元素(最大值),插入到最小堆。
- 如果两个堆的大小不平衡,调整使得两个堆的大小相差不超过1。
- 获取中位数的操作可以根据两个堆的大小分情况返回。
代码实现
import java.util.ArrayDeque;
import java.util.Deque;
class Solution {
public int largestRectangleArea(int[] heights) {
Deque<Integer> stack = new ArrayDeque<>();
int maxArea = 0;
for (int i = 0; i <= heights.length; i++) {
int h = (i == heights.length) ? 0 : heights[i];
if (stack.isEmpty() || h >= heights[stack.peek()]) {
stack.push(i);
} else {
while (!stack.isEmpty() && h < heights[stack.peek()]) {
int top = stack.pop();
int width = stack.isEmpty() ? i : i - 1 - stack.peek();
maxArea = Math.max(maxArea, heights[top] * width);
}
stack.push(i);
}
}
return maxArea;
}
}