C语言中的七种常用排序

news2024/9/20 18:34:58

今天，为大家整理了C语言中几种常用的排序，以及他们在实际中的运用（有Bug请在下方评论）：

一.桶排序

#include <stdio.h>
int main()
{
    int book[1001],i,j,t,n;
    for(i=0;i<=1000;i++)
        book[i]=0;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
    {
        scanf("%d",&t);
        book[t]++;
    }
    for(i=1000;i>=0;i--)
        for(j=1;j<=book[i];j++)
            printf("%d ",i);
    getchar();getchar();
    return 0;
}

桶排序是一种快速简单的排序，但实用性不强。工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。 

二.冒泡排序

void bubblesort(int arr[], int sz)
{
    int i = 0;
    for (i = 0; i < sz-1;i++)
    {
        int j = 0;
        for (j = 0; j < sz - 1 - i; j++)
        {
            if (arr[j] > arr[j + 1])
            {
                int tmp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = tmp;
            }
        }
    }
}
void print_arr(int arr[], int sz)
{
    int i = 0;
    for (i = 0; i < sz; i++)
    {
        printf("%d ", arr[i]);
    }
}
int main()
{
    int arr[10] = { 9,8,7,6,5,4,3,2,1,0 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    bubble_sort(arr, sz);
    print_arr(arr, sz);
}

*冒泡排序核心部分是双重for循环，故空间占用较大。

冒泡排序的原理是：从左到右，相邻元素进行比较。每次比较一轮，就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。

三.快速排序

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Quick_Sort(int a[], int l, int r) {
	if (l < r) {
		int i, j, x;
		i = l;
		j = r;
		x = a[i];
		while(i<j) {
			while (i<j && a[j]>x) {
				j--; 
			}
			if (i < j) {
				a[i++] = a[j];
			}
			while (i < j && a[i] < x) {
				i++; 
			}
			if (i < j) {
				a[j--] = a[i]; 
			}
		}
		a[i] = x;
		Quick_Sort(a, l, i - 1);
		Quick_Sort(a, i+1, r);
	}
}
 
int main() {
	int arr[] = { 9,5,1,6,2,3,0,4,8,7 };
	Quick_Sort(arr, 0, 9);
	for (int i = 0; i < 10; i++) {
		printf("%d ", arr[i]);
	}
	printf("\n");
 
	return 0;
}

快速排序是最常用的一种排序，其思路为：

假设一个数组，我们可以用一种办法分成小数块和大数块，然后递归继续分成小数块和大数块，最后每一块都只有1个(或者0个)的时候，排序就完成了 

四.计数排序

//注：引用自DYson~的博客
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
//计数排序
void CountSort(int *a, int len)
{
	assert(a);
	//通过max和min计算出临时数组所需要开辟的空间大小
	int max = a[0], min = a[0];
	for (int i = 0; i < len; i++){
		if (a[i] > max)
			max = a[i];
		if (a[i] < min)
			min = a[i];
	}
	//使用calloc将数组都初始化为0
	int range = max - min + 1;
	int *b = (int *)calloc(range, sizeof(int));
	//使用临时数组记录原始数组中每个数的个数
	for (int i = 0; i < len; i++){
		//注意：这里在存储上要在原始数组数值上减去min才不会出现越界问题
		b[a[i] - min] += 1;
	}
	int j = 0;
	//根据统计结果，重新对元素进行回收
	for (int i = 0; i < range; i++){
		while (b[i]--){
			//注意：要将i的值加上min才能还原到原始数据
			a[j++] = i + min;
		}
	}
	//释放临时数组
	free(b);
	b = NULL;
}
//打印数组
void PrintArray(int *a, int len)
{
	for (int i = 0; i < len; i++){
		printf("%d ", a[i]);
	}
	printf("\n");
}
int main()
{
	int a[] = { 3, 4, 3, 2, 1, 2, 6, 5, 4, 7 };
	printf("排序前：");
	PrintArray(a, sizeof(a) / sizeof(int));
	CountSort(a, sizeof(a) / sizeof(int));
	printf("排序后：");
	PrintArray(a, sizeof(a) / sizeof(int));
	system("pause");
	return 0;
}

计数排序的基本思想是对于给定的输入序列中的每一个元素 x，确定该序列中值小于 x 的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将 x 直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有 17 个元素的值小于 x 的值，则 x 可以直接存放在输出序列的第 18 个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

五.基数排序

#include <stdio.h>
#include <assert.h>
#include <math.h>
#include <stdlib.h>
 
typedef struct Node
{
    int data;
    struct Node *next;
}Node,*List;
 
void InitList(Node *plist)
{
    assert(plist != NULL);
    plist->next = NULL;
}
 
Node *GetNode(int val)
{
    Node *pGet = (Node *)malloc(sizeof(Node));
    assert(pGet !=NULL);
 
    pGet->data = val;
    pGet->next = NULL;
    return pGet;
}
 
void Insert_tail(Node *plist,int val)
{
    assert(plist != NULL);
 
    Node *p = plist;
    while (p->next != NULL)
    {
        p = p->next;
    }
    Node *pGet = GetNode(val);
    p->next = pGet;
}
 
bool DelHeadNode(Node *plist,int *res)
{
    assert(plist != NULL);
 
    Node *pDel = plist->next;
    if (pDel == NULL)
    {
        return false;
    }
 
    *res = pDel->data;
    plist->next = pDel->next;
    free(pDel);
    pDel = NULL;
    return true;
}
 
int GetMaxBit(int *arr, int length)
{
    assert(arr != NULL);
    int max = INT_MIN;
    for (int i = 0; i < length; i++)
    {
        if (arr[i] > max)
        {
            max = arr[i];
        }
    }
    int digit = 0;
    while (max != 0)
    {
        digit++;
        max /= 10;
    }
    return digit;
}
 
int GetNum(int num, int figures)   // 123   123 / 1 % 10 == 3      123 / 10 % 10 == 2   123 / 100 % 10 == 1   
{
    int base = pow((double)10,(figures));
    return num / base % 10;
}
 
 
//figures --> 从右往左数第figures位的数字
void Radix(int *arr,int length,int figures)
{
    Node head[10];
    for (int i = 0; i < 10; i++)
    {
        InitList(&head[i]);  // 初始化10个桶
    }
 
    int tmp = 0;
    // 1、入桶 == 》 拿到数字，判断第figures位的数字为多少，并入相应的桶
    int i = 0;
    for (; i < length; i++)
    {
        tmp = GetNum(arr[i],figures);  // 第figures位的数字为tmp
        Insert_tail(&head[tmp],arr[i]); // 将 arr[i] 出到 tmp桶中
    }
 
    // 2、出桶
    i = 0; // i 代表数组下标
    int j = 0;
    while (j < 10)    // j 代表桶的个数
    {
        while (DelHeadNode(&head[j],&arr[i])) 
        {
            i++;
        }
        j++;
    }
}
 
 
void RadixSort(int *arr, int length)
{
    int count = GetMaxBit(arr ,length);
    for (int i = 0; i < count; i++)
    {
        Radix(arr,length,i);
    }
}
 
void Show(int *arr, int length)
{
    for (int i = 0; i < length; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
}
 
 
void test(int *arr, int length)
{
    RadixSort(arr,length);
    Show(arr,length);
}
 
void test1()
{
    int arr[] ={1,2,3,4,12,4444,2222,1112,11};
    int length = sizeof(arr)/sizeof(arr[0]);
    test(arr,length);
}
 
void test2()
{
    int arr[] ={336,719,329,170,66,511,36,519,200,504};
    int length = sizeof(arr)/sizeof(arr[0]);
    test(arr,length);
}
 
int main()
{
    test1();
    test2();
    return 0；
}

基数排序与桶排序思路相仿，但优化了许多（也麻烦了许多，不太建议日常使用）

六.插入排序

示意图： 

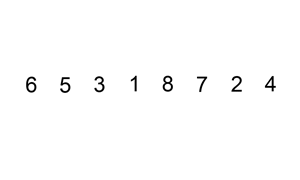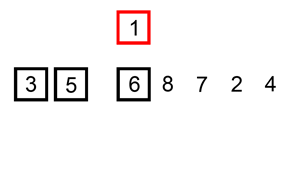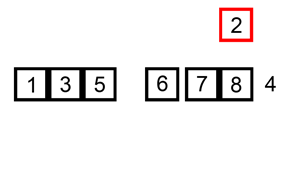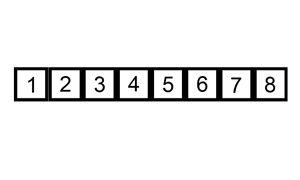
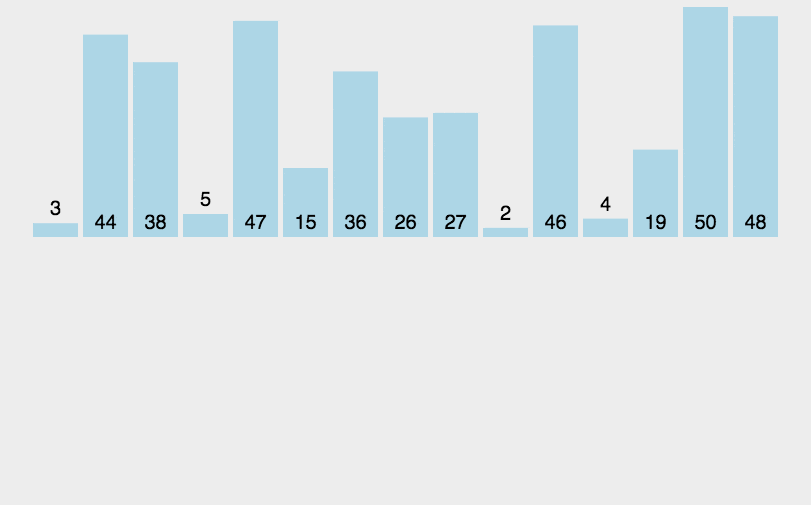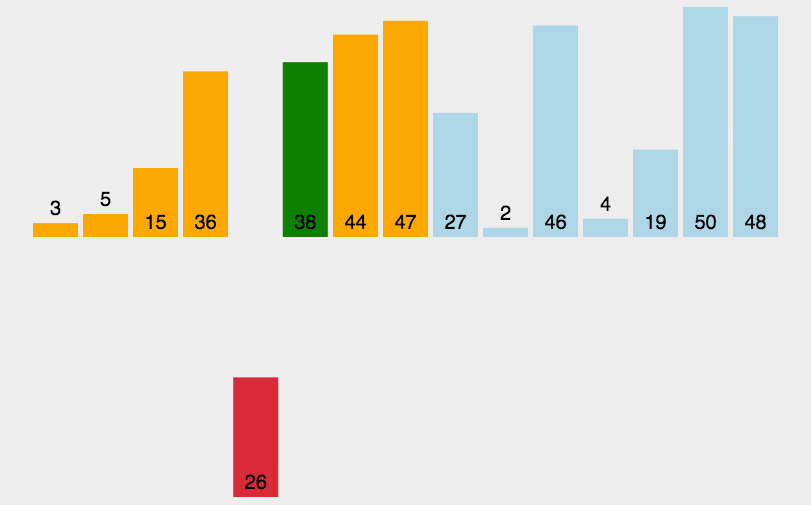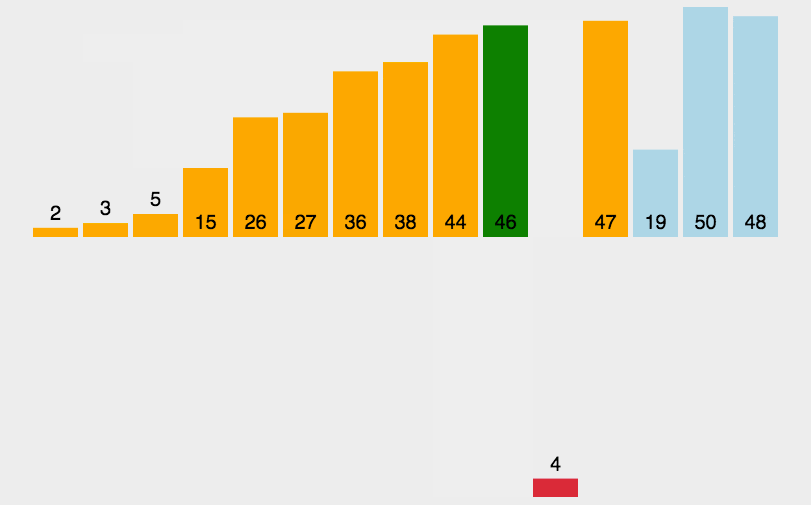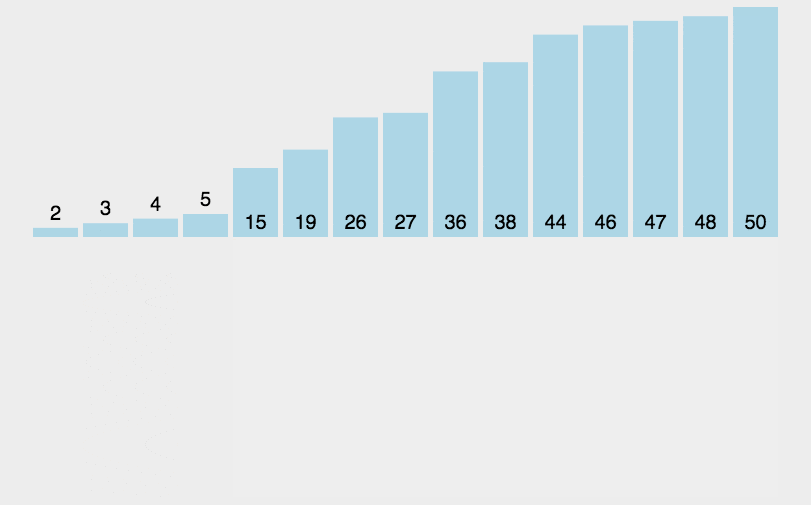
//插入排序(从小到大) 
#include<stdio.h>
#include<stdlib.h>
int number[100000000];     //定义数组 
void insertion_sort(int *number,int n)    //定义一个插入函数"insertion_sort" 
{
    int i,t,temp;  
    for(i=1;i<n;i++)  //外层循环遍历 （需要插入n个数）
    {
        temp=number[i];  //取未排序列的元素，有n个，从第一个开始取
        for(t=i;t>0&&number[t-1]>temp;t--);
		{
			number[t]=number[t-1];//依次比较并右移
			number[t]=temp;//放进合适位置
		}
	}
}
int main() 
{
    int i=0,n,j=0;
    printf("输入数字个数：\n");    
    scanf("%d",&n);       //输入要排序的数字的个数 
    printf("输入%d个数:\n",n);
    for(j=0;j<n;j++)       //将所有数全放入number数组中 
        scanf("%d",&number[j]) ;
    insertion_sort(number,n);   //引用插入函数 
    for(i=0;i<n-1;i++)    //循环输出 
        printf("%d ",number[i]);    //格式需要  
    printf("%d\n",number[i]);
	system("pause");
    return 0;
}

 插入排序其实就是拿未排序数组中的第一个值，插入到已排序完中的数组的合适位置，来完成排序

七.堆排序

#include <stdio.h>
#include <malloc.h>
void HeapAdjust(int a[],int s,int m)//一次筛选的过程
{
    int rc,j;
    rc=a[s];
    for(j=2*s;j<=m;j=j*2)//通过循环沿较大的孩子结点向下筛选
    {
        if(j<m&&a[j]<a[j+1]) j++;//j为较大的记录的下标
        if(rc>a[j]) break;
        a[s]=a[j];s=j;
    }
    a[s]=rc;//插入
}
void HeapSort(int a[],int n)
{
    int temp,i,j;
    for(i=n/2;i>0;i--)//通过循环初始化顶堆
    {
        HeapAdjust(a,i,n);
    }
    for(i=n;i>0;i--)
    {
        temp=a[1];
        a[1]=a[i];
        a[i]=temp;//将堆顶记录与未排序的最后一个记录交换
        HeapAdjust(a,1,i-1);//重新调整为顶堆
    }
}
int main()
{
    int n,i;
    scanf("%d",&n);
    int a[n+1];
    for(i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    HeapSort(a,n);
}

堆排序的思想基于二叉树，比较麻烦

堆排序方法对记录较少的文件并不值得提倡，但对n较大的文件还是很有效的。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1697073.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

B树与B+树区别

B树与B+树区别

B树和B树是常见的数据库索引结构&#xff0c;都具有相较于二叉树层级较少&#xff0c;查找效率高的特点&#xff0c;它们之间有以下几个主要区别&#xff1a; 1.节点存储数据的方式不同 B树的叶子结点和非叶子节点都会存储数据&#xff0c;指针和数据共同保存在同一节点中B树…
阅读更多...
MySQL的索引, 到底怎么创建?

MySQL的索引, 到底怎么创建?

目录 前言 MySQL的数据结构 索引是一把双刃剑 索引创建原则 如何给一个列挑选索引? 索引列的基数, 要尽量小 索引列的类型尽量小 索引长字符串的前缀 不要对索引列进行计算操作或者函数计算. 不要老想着查询, 想想插入该怎么办? 避免索引冗余和重复 前言 今天在…
阅读更多...
【二叉树】：LeetCode：100.相同的数(分治）

【二叉树】：LeetCode：100.相同的数(分治）

&#x1f381;个人主页&#xff1a;我们的五年 &#x1f50d;系列专栏&#xff1a;初阶初阶结构刷题 &#x1f389;欢迎大家点赞&#x1f44d;评论&#x1f4dd;收藏⭐文章 1.问题描述&#xff1a; 2.问题分析&#xff1a; 二叉树是区分结构的&#xff0c;即左右子树是不一…
阅读更多...
上5个B端系统的设计规范，让你的开发比着葫芦画瓢。

上5个B端系统的设计规范，让你的开发比着葫芦画瓢。

B端系统设计规范在企业级系统开发中起着重要的作用&#xff0c;具体包括以下几个方面&#xff1a; 统一风格和布局&#xff1a;设计规范能够统一系统的风格和布局&#xff0c;使不同功能模块的界面看起来一致&#xff0c;提升用户的使用体验和学习成本。通过统一的设计规范&am…
阅读更多...
模型驱动架构设计方法及应用

模型驱动架构设计方法及应用

引言 模型驱动架构&#xff08;Model Driven Architecture&#xff0c;MDA&#xff09;是一种软件开发方法论&#xff0c;它强调使用一系列抽象层次的模型&#xff0c;并利用模型之间的转换来实现从需求到设计、直至代码生成的全过程。MDA的核心思想是在软件开发过程中强调使用…
阅读更多...
druid 1.2.14，application.yaml配置文件中，如何进行数据库加密配置

druid 1.2.14，application.yaml配置文件中，如何进行数据库加密配置

步骤一&#xff1a;先生成加密的密码&#xff1a; 步骤二&#xff1a;配置application.yaml文件&#xff1a; spring:datasource:driver-class-name: com.mysql.cj.jdbc.Drivertype: com.alibaba.druid.pool.DruidDataSourcedruid:username: rootpassword: aPJ35saFz6ASmnmNt…
阅读更多...
CentOS 7.9部署宝塔面板超详细

CentOS 7.9部署宝塔面板超详细

CentOS7 部署宝塔面板 Linux的宝塔面板搭建起来非常轻松&#xff0c;也可以用一句话来形容&#xff0c;如果喝水一样简单&#xff0c;只需一条命令剩下的交给时间&#xff0c;几分钟就能部署好&#xff0c;然后就可以直接进行登录&#xff0c;直接可以安装LNMP、LAMP平台&…
阅读更多...
数据结构与算法（Java版） | 详解十大经典排序算法之一：希尔排序

数据结构与算法（Java版） | 详解十大经典排序算法之一：希尔排序

接下来&#xff0c;我来给大家讲解第四种排序算法&#xff0c;即希尔排序。 简单插入排序所存在的问题 在上篇文章中&#xff0c;我已经给大家讲解完插入排序了&#xff0c;虽说是讲完了&#xff0c;但在这里我还是想请大家开动脑筋思考一下&#xff0c;就是咱们讲解的插入排…
阅读更多...
SDK崩溃后怎么打开已有工程

SDK崩溃后怎么打开已有工程

1.进到SDK里面&#xff0c;保留&#xff1a;platform、bsp和工程包&#xff08;这里是C&#xff09;&#xff0c;其他都删掉 2.windows窗口运行sdk 3.导入sdk工程
阅读更多...
基于springboot+vue的4S店车辆管理系统

基于springboot+vue的4S店车辆管理系统

开发语言&#xff1a;Java框架&#xff1a;springbootJDK版本&#xff1a;JDK1.8服务器&#xff1a;tomcat7数据库&#xff1a;mysql 5.7&#xff08;一定要5.7版本&#xff09;数据库工具&#xff1a;Navicat11开发软件&#xff1a;eclipse/myeclipse/ideaMaven包&#xff1a;…
阅读更多...
人工智能场景下的网络负载均衡技术

人工智能场景下的网络负载均衡技术

AI技术驱动智能应用井喷&#xff0c;智能算力增速远超通用算力。IDC预测&#xff0c;未来五年&#xff0c;我国智能算力规模年复合增长率将超50%&#xff0c;开启数据中心算力新纪元。随着需求激增&#xff0c;数据中心或智算网络亟需扩容、增速、减时延&#xff0c;确保网络稳…
阅读更多...
数据结构（三）栈 队列 数组

数据结构（三）栈 队列 数组

2024年5月26日一稿（王道P78） 栈 基本概念 基本操作 顺序存储结构 基本操作 共享栈
阅读更多...
数据库管理-第194期 网络加速RDMA初探（20240526）

数据库管理-第194期 网络加速RDMA初探（20240526）

数据库管理194期 2024-05-26 数据库管理-第194期 网络加速RDMA初探&#xff08;20240526&#xff09;1 概念2 发展3 使用总结 数据库管理-第194期 网络加速RDMA初探&#xff08;20240526&#xff09; 作者&#xff1a;胖头鱼的鱼缸&#xff08;尹海文&#xff09; Oracle ACE A…
阅读更多...
PLSQL连接Linux Oracle21c

PLSQL连接Linux Oracle21c

PLSQL连接Linux Oracle21c 一、安装PLsql 下载官网 https://www.allroundautomations.com/registered-plsqldev/ 二、Oracle Instant Client下载 使用plsql连接oracle的时候是需要本地先安装oracle客户端&#xff0c;英文名就是Oracle Instant Client。 官方下载地址&…
阅读更多...
RedHat9 | DNS剖析-配置辅助DNS服务器

RedHat9 | DNS剖析-配置辅助DNS服务器

一、实验环境 1、辅助域名DNS服务器 DNS通过划分为若干个区域进行管理&#xff0c;每一个区域由1台或多台DNS服务器负责解析&#xff0c;如果仅仅采用1台DNS服务器&#xff0c;在DNS服务器出现故障后&#xff0c;用户将无法完成解析。 辅助DNS服务器的优点 容灾备份&#x…
阅读更多...
PaddleSeg训练推理及模型转换全流程

PaddleSeg训练推理及模型转换全流程

文章目录 1、数据准备1.1 数据标注1.2 数据导出1.3 标签较验1.4 数据集整理1.5 标签可视化 2、 模型训练3、模型验证4、模型推理5、模型导出6、导出文件的推理7、将模型转换成onnx8、使用onnx进行推理 本文记录一下使用paddleseg进行语议分割模型对人体进行分割的使用流程。事实…
阅读更多...
自然资源-各级国土空间总体规划的审查要点及流程总结

自然资源-各级国土空间总体规划的审查要点及流程总结

自然资源-各级国土空间总体规划的审查要点及流程总结 国土空间规划是对一定区域国土空间开发保护在空间和时间上作出的安排&#xff0c;包括总体规划、详细规划和相关专项规划。 国土空间规划管理是国土空间规划中重要的一环。中共中央、国务院发布《关于建立国土空间规划体系…
阅读更多...
数据与结构--AVL树

数据与结构--AVL树

目录 AVL树的概念 AVL树的性质 AVL树结点的定义 AVL树的插入 AVL树的旋转 左单旋 右单旋 左右双旋 右左单旋 AVL树的验证 AVL树的查找 AVL树的修改 AVL树的删除 AVL树的概念 二叉搜索树虽然可以提高我们查找数据的效率&#xff0c;但如果插入二叉搜索树的数据是…
阅读更多...
福昕PDF使用技巧

福昕PDF使用技巧

因为突然间学校的企业版WPS突然很多功能就不能使用了&#xff0c;所以转向福昕PDF。 一、合并文件 添加需要合并的文件&#xff0c;可以使用ctrla等方式全选 找到最上方的“合并文件” 二、文本注释
阅读更多...
linux中最常用的文件管理命令

linux中最常用的文件管理命令

linux中最常用的文件管理命令 linux中最常用的文件管理命令最常用的且没有之一的 ls命令格式不加任何参数使用-l显示更多细节使用-t按照时间排序使用-r按照时间逆序使用-S根据文件大小排序 查看庐山真面貌的cat实例 &#xff1a;简单显示内容实例 &#xff1a;显示行号 -n实例 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023