数据结构与算法（Java版） | 详解十大经典排序算法之一：希尔排序

接下来，我来给大家讲解第四种排序算法，即希尔排序。

简单插入排序所存在的问题

在上篇文章中，我已经给大家讲解完插入排序了，虽说是讲完了，但在这里我还是想请大家开动脑筋思考一下，就是咱们讲解的插入排序有没有什么所谓的问题。这里，我就直接跟大家说了，肯定是存在问题的，至于是什么问题，下面我就来给大家分析。

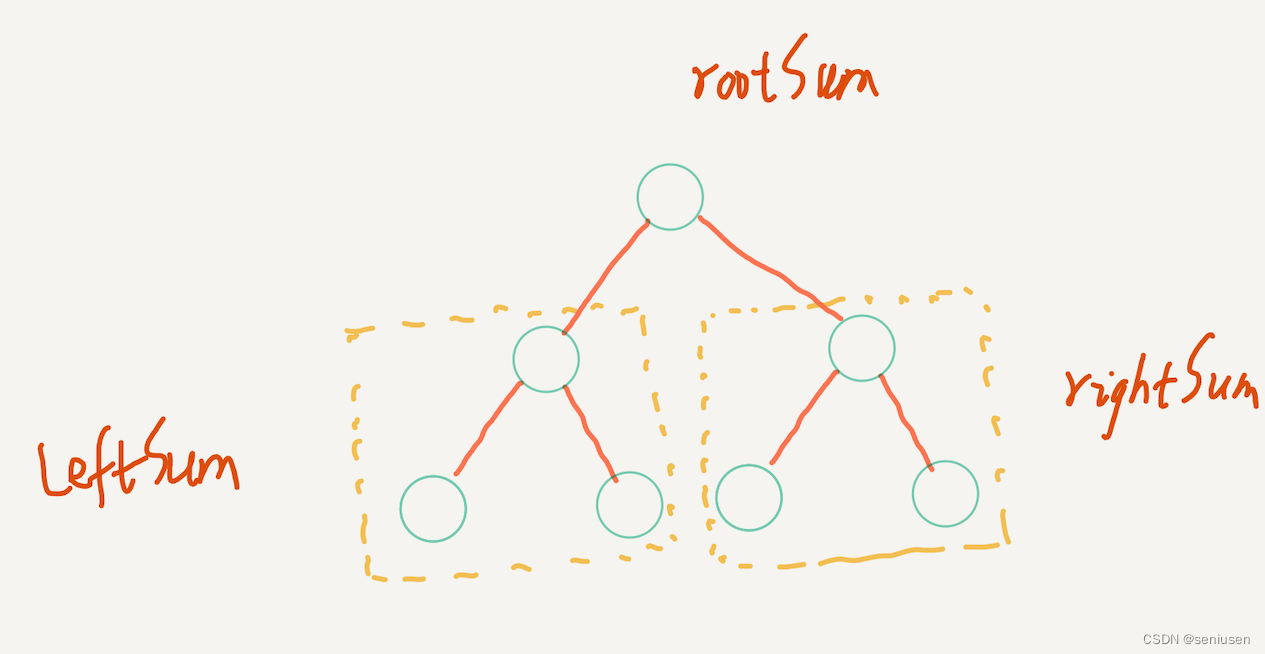
假设现在有{2, 3, 4, 5, 6, 1}这样一个数组，如果此时此刻我们想为1（数组里面的最小元素）进行插入，那么插入的过程是不是就应该是下面这个样子啊！

由于待插入数（即1）小于有序表最后那个元素（即6），因此我们会让6后移，这样，待排序数组就变成{2, 3, 4, 5, 6, 6}这个样子了；
同上，5也会后移，后移之后，待排序数组就变成{2, 3, 4, 5, 5, 6}了；
同上，4也会后移，后移之后，待排序数组就变成{2, 3, 4, 4, 5, 6}了；
同上，3也会后移，后移之后，待排序数组就变成{2, 3, 3, 4, 5, 6}了；
同上，2也会后移，后移之后，待排序数组就变成{2, 2, 3, 4, 5, 6}了；
最后，当退出while循环时，说明我们已然找到了待插入数（即1）它所要插入的那个位置，也即索引0处，找到之后，那我们自然就是要进行插入了，插毕，待排序数组就变成{1, 2, 3, 4, 5, 6}这个样子了，也就是说，此刻待排序数组才变得有序。

经过以上分析，相信大家应该不难得知这样一个结论吧，即在进行插入排序时，如果我们假定是要按从小到大的顺序来排序，那么当需要插入的数是较小的数时，后移的次数就会明显增多，随之而来的，便是效率就会受到影响了。而这也从另一方面说明，我们在考虑一个算法的时候，必须去考虑到它最差的那种情况，是不是啊！

以上就是简单插入排序可能存在的一个问题。而正是鉴于此，我们才提出了另外一种排序算法，即希尔排序，可以这样说，希尔排序是我们对简单插入排序优化之后的一种排序算法。

基本介绍

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。不置可否，希尔排序也是一种插入排序，而且它是简单插入排序经过改进之后的一个更高效的版本，当然，你也可以把它称为缩小增量排序。

基本思想

简单认识希尔排序之后，接下来我就要来给大家详细说说它的排序思想了。

希尔排序的基本思想是这样子的，即希尔排序是把记录按下标的一定增量分组，分组之后，再来对每一组使用直接插入排序算法进行排序；而随着增量的逐渐减少，每一组包含的关键词也将会越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止了。

可能我这样讲，有些同学会觉得比较抽象，不过没关系啊，下面我会给大家看一个希尔排序的思路图解，相信大家看完过后自然就会明白我上面讲的希尔排序的基本思想了。

说啊，目前有一个数组，它的初始状态是下面这样子的。

在这里插入图片描述

从上可以看到，咱们的原始数组一共有10个元素，而且还没有顺序，是不是啊，此外，它里面最小的那个元素（即0）还被我们放在了最后，这是不是就符合上面我们所说的简单插入排序可能会存在问题的这样一个情况啊！因此，这里我们就不能再使用简单插入排序算法了，那不使用简单插入排序算法，应该使用什么呢？使用简单插入排序经过改进之后的一个更高效的版本的排序算法，即希尔排序。

注意，这里还有一点我得给大家说明一下，就是我画的希尔排序的思路图解中，你看到的那些颜色相同的数据元素，它们是一组的。

废话不多说，接下来，我们来针对以上数组进行希尔排序。

首先，将初始增量置为arr.length / 2，即数组的大小除以2，很明显，这儿就是5，初始增量为5，大家知道这意味着什么吗？意味着整个原始数组得被我们分成5组，即{8, 3}、{9, 5}、{1, 4}、{7, 6}、{2, 0}。

在这里插入图片描述

注意，分组时，我们并不是按照顺序来分的，也即不是说8和9我们分为一组，1和7我们再分为一组，后面依此类推，而之所以不这样分，是因为这样分没有丝毫意义。既然不是按照顺序来分，那又应该怎么分呢？其实，从上图中大家应该就能看出来，分组时我们是利用步长（就是初始增量5）来分的，是不是啊！

上面我们分好组之后，接下来我们就要对这5组分别来进行直接插入排序了。大家看一下，完事过后，待排序数组是不是就变成下面这个样子了！

在这里插入图片描述

应该很好理解吧，你想啊，{8, 3}这组进行直接插入排序，是不是3得插到8的前面啊，同理，后面几组进行直接插入排序，也是这样一个道理，非常简单，因此这里我就不再过多赘述了。

不知道大家有没有发现这一点，就是以上5组数据经直接插入排序之后，像3、5、6这些小元素都被我们调到前面来了，是不是啊，而这也从另一方面说明了，较小元素会被我们快速地弄到前面来。

然后，缩小增量至5 / 2，即2，因为我们得取整嘛！缩小增量至2，大家知道这意味着什么吗？意味着以上数组又得被我们分成2组，即{3, 1, 0, 9, 7}和{5, 6, 8, 4, 2}。

在这里插入图片描述

很明显，此时我们又得来对这2组分别进行直接插入排序。大家看一下，完事过后，待排序数组是不是就变成下面这个样子了！

在这里插入图片描述

从上可以看到，此时整个数组的有序程度又进了一步。

接着，再缩小增量至2 / 2，即1，很明显，此时，整个数组就只能被我们分成1组了。

在这里插入图片描述

可以看到，经过上面的“宏观调控”，整个数组的有序化程度成果越来越喜人了。

此时，仅仅需要对以上数组简单微调，无需大量移动操作即可完成整个数组的排序。

在这里插入图片描述

总之，随着增量的逐渐缩小，整个数组会越来越接近于一个有序数列，当增量缩减至1时，整个数组恰被分成一组，此时我们仅仅需要对该数组做一次直接插入排序即可完成整个数组的排序，而且还不需要大量后移操作哟！

以上就是我们对希尔排序的一个介绍以及其基本思想的讲解。至于接下来要干嘛，相信大家也都知道了，无非就是来编写具体代码用以实现希尔排序。

代码实现

先来看这样一个案例，说是班级里面有一群小朋友，他们的考试成绩分别是8、9、1、7、2、3、5、4、6和0，现请你对他们的考试成绩按照从小到大的顺序进行排序。

以上案例，相信大家也不难理解其需求，无非就是对一个数组进行希尔排序罢了。

注意，这里有一点我得向大家说明一下，就是使用希尔排序，在对有序序列进行插入时，其实是有两种方式可供我们选择的，一种是交换法，这种方式比较好理解，但就是速度相对较慢；另一种是移动法，这种方式相对不太好理解，但效率会较高。

之所以我在这里要向大家说明这点，是因为待会我们使用希尔排序时，会分别采用这两种方式（即交换法和移动法）来对有序序列进行插入。当然，这里我会先向大家讲解交换法这种方式，因为这种方式比较好理解嘛，等讲解完毕之后，我们再来将其优化成移动法，相信我这样子讲解对大家理解希尔排序应该是非常有帮助的吧！最后，大家千万不要忘了在排序完毕之后来对排序速度进行一个测试哟！