前缀和算法：提升编程效率的秘密武器(Java版)

本篇会加入个人的所谓鱼式疯言

❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言
而是理解过并总结出来通俗易懂的大白话,
小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.
🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 ！！！

在这里插入图片描述

前言

在前面我们熟悉了 == “双指针” 算法== ，== “滑动窗口” 算法==，以及 二分查找 算法。小伙伴可以思考下，

这些本质上是不是都是双指针呢，没错，当然是的 💖 💖 💖

这三个专题我们已经 圆满结束啦, 那么我们的双指针大家族也算是告一段落啦 💖 💖 💖

而在本篇我们中讲新的专题，是去双指针不同的专题， 前缀和 算法

下面小伙伴先了解下本篇文章的规划吧 😊 😊 😊

一. 前缀和算法的初识

<1>. 前缀和算法的简介

前缀和算法，也称为 前缀和技巧 ，是一种常见的算法技巧，用于高效地计算数组或序列中某个 位置前 的 所有元素的和。

前缀和算法的思路是先计算出从数组的起始位置到每个位置的 子数组和 ，然后根据需要的范围计算出相应的结果。

<2>. 前缀和使用流程

我们通过一个简单的题目来讲解前缀和的具体使用吧 💖 💖 💖 💖

1. 前缀和

DP34.前缀和题目链接

<1>. 题目描述

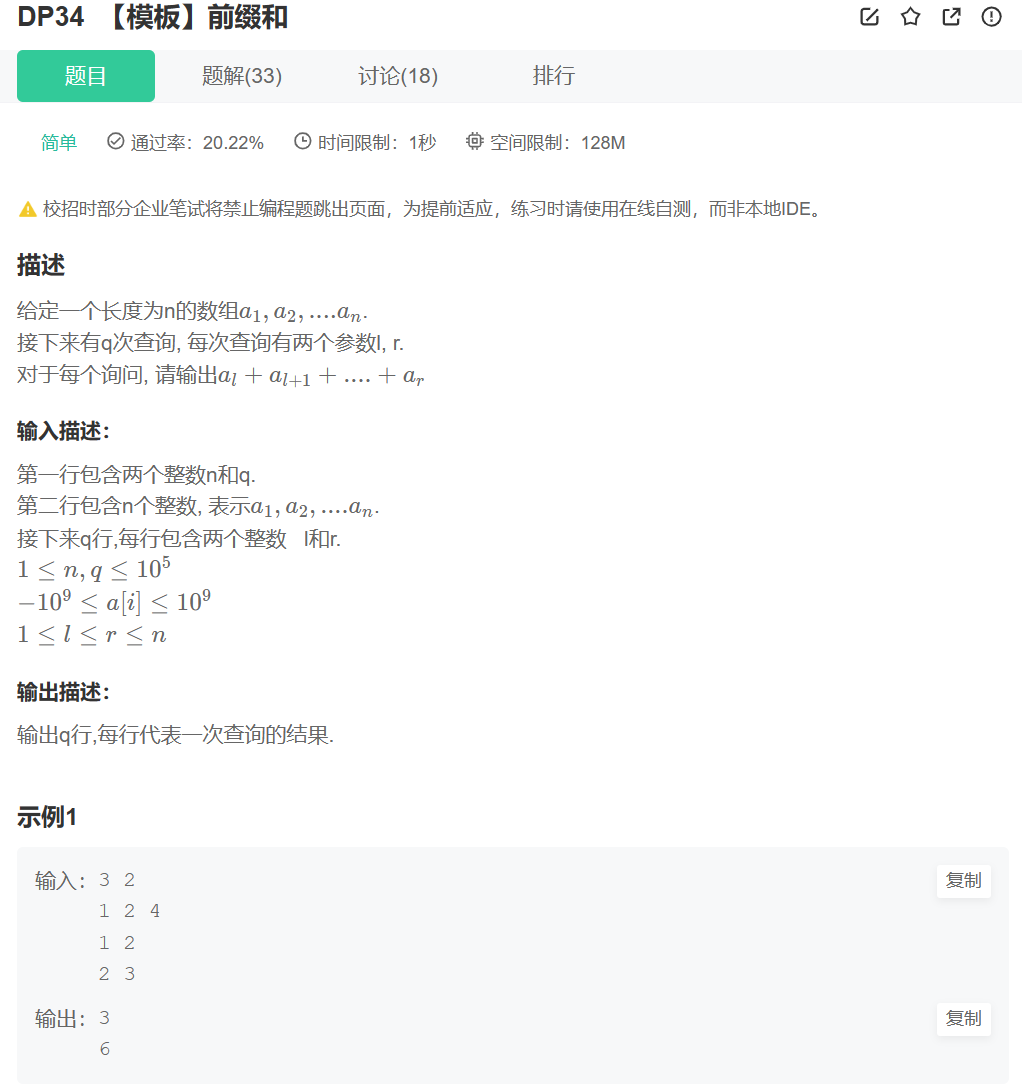
在这里插入图片描述

题目含义：

先 初始化一个数组，并 指定长度，然后在指定一段需要求的 子数组的区间 的总和，进行返回，注意这里要指定 q 次, 意味着我们要求 q 次子数组的总和并返回

<2>. 讲解算法思想

题目分析 ：

遇到求某段区间的总和，我们不难想到

解法一 :

暴力求解

用一个 for 循环来累加左右区间的，然后循环往复进步 q 次

前缀和算法 :

我们先定义一个 数组dp，这个数组是主要用来统计 i 位置到 0 的元素的总和

算法步骤

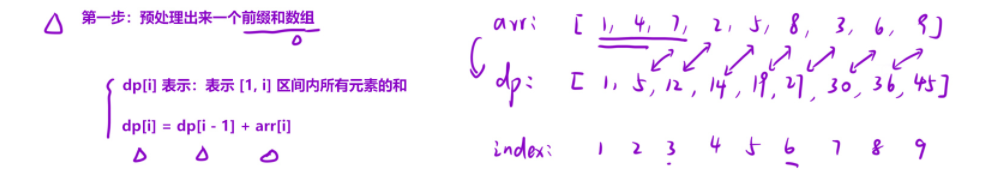
在这里插入图片描述

第一步：先定义 dp 数组， i = 0 时，先把第一个元素进行 相加，然后到 i = 1 时，我们就在 dp[0] 的基础上加上原数组(假设原数组名为 nums ) nums[1] 那个元素 , 循环往复，意味着就可以得到我们的 每个位置到 0 位置的总和的数据。

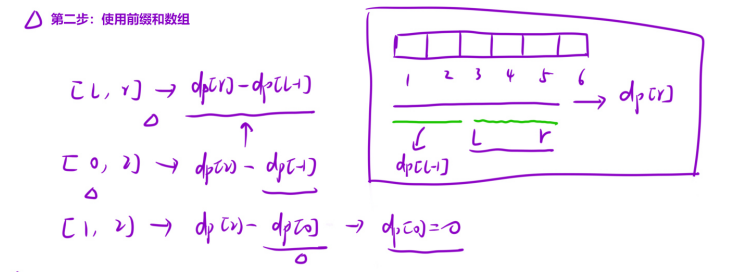
在这里插入图片描述

第二步：使用前缀和数组，我们要得到某得区间的，就可以利用前缀和数组，用 dp[右边界] - dp[左边界-1] 就可以得到我们的该区间的和

请添加图片描述

<3>. 编写代码

import java.util.Scanner;




// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {

    public static void main(String[] args) {
        
        
        Scanner in = new Scanner(System.in);
        
        
        int n=in.nextInt();
        int q=in.nextInt();
       

       long [] array=new long [n+1];
       for(int i =1 ; i < n+1 ; ++i) {
            
            array[i]=in.nextInt();      
       
       }

        int k=0;
        
        long[] sum=new long[q];
        long[] dp=new long[n+1];
        dp[0]=0;
        for(int x= 1; x < n+1 ; x++ ) {
            dp[x]= dp[x-1] + array[x];
        }
       
       while(q != 0) {
            
            int left = in.nextInt();
            
            int right = in.nextInt();
             
                
                System.out.println(dp[right]-dp[left-1]);                
             

            k++;
            
            q--;
       
       }



   

    }


}

在这里插入图片描述

鱼式疯言

前缀和算法的时间复杂度为 O(n) ，其中 n 表示数组的长度。

它的主要应用场景包括计算连续子数组的和、找到和为某个特定值的 子数组等 。

细节处理 ：

 dp[0]=0;

我们这里就直接放置 下标 0 的位置为 0 ，这样就可以有序的进行循环 dp[i]= dp[i-1] +array[i];

在这里插入图片描述

因为当 i=0 ， i-1 就很有可能 发生越界

二. 前缀和的实际运用

1. 除自身以外的乘积

238.除自身以外的乘积题目链接

<1>. 题目描述

在这里插入图片描述

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

题目含义 ：

定义一个新数组，求 nums 除了该位置以外元素的 乘积，并赋值给新数组的当前位置

<2>. 讲解算法思想

题目分析 :

因为题目要求我们不能使用 除法 ，

所以就要利用 前缀积 算法, 并且使用 前缀积 和 后缀积 结合起来去解决本题

在这里插入图片描述

算法步骤

首先我们需要两个数组一个是前缀积 dpleft 和 dpright ；来 （同一下标） 初始化我们的 前缀积 以及 后缀积

当我们定义 前缀积 时：

从 下标 0 开始 从左往右 累加 dp[i]= dp[i-1] * nums[i-1] 初始化 deleft数组

请添加图片描述

当我们定义后缀积deright 从 nums最后一个数组 从右往左 开始（同一下标） dp[i] = dp[i + 1] * nums[i + 1] 来初始化 后缀和deright

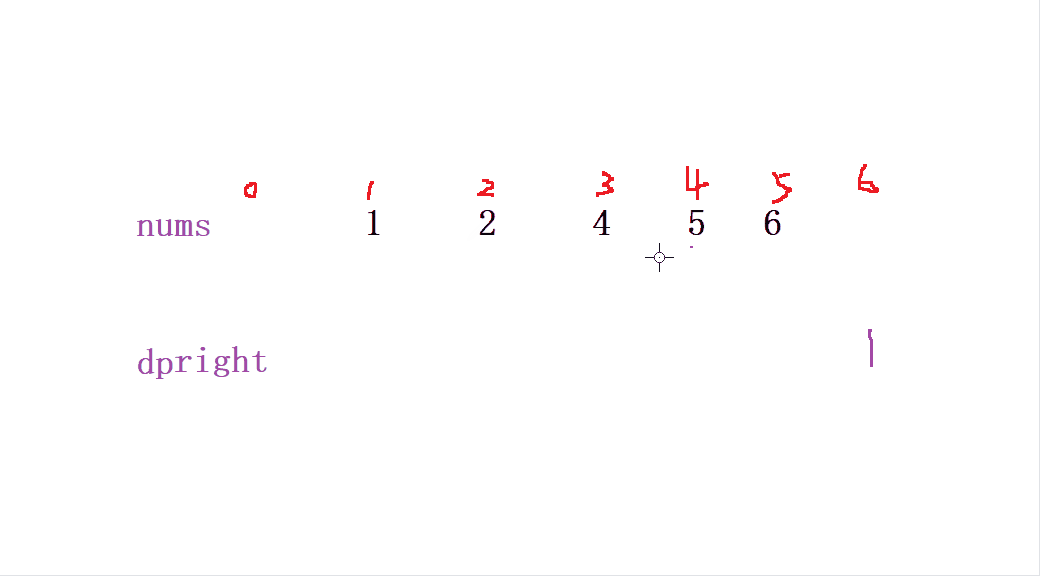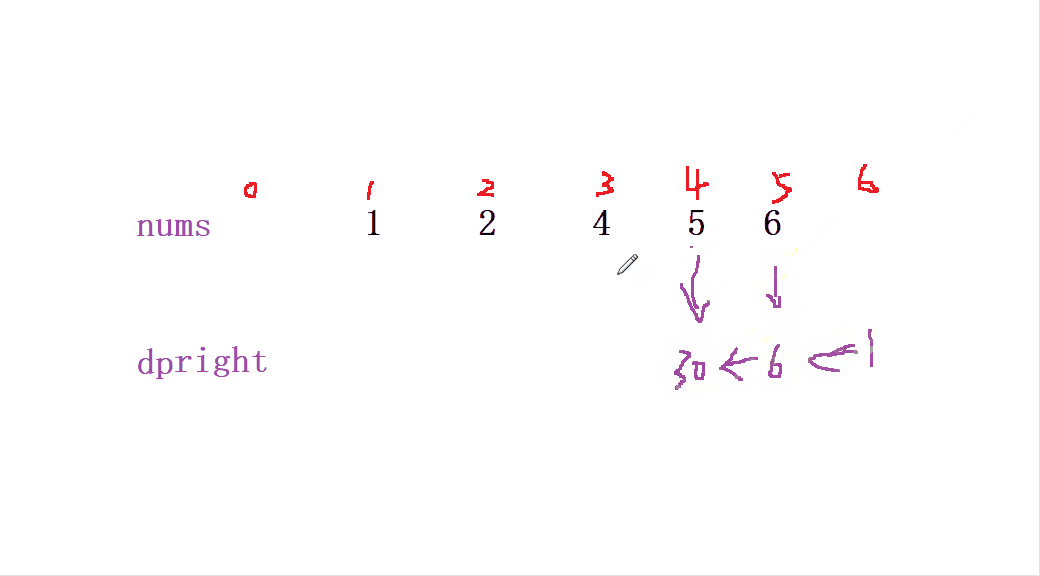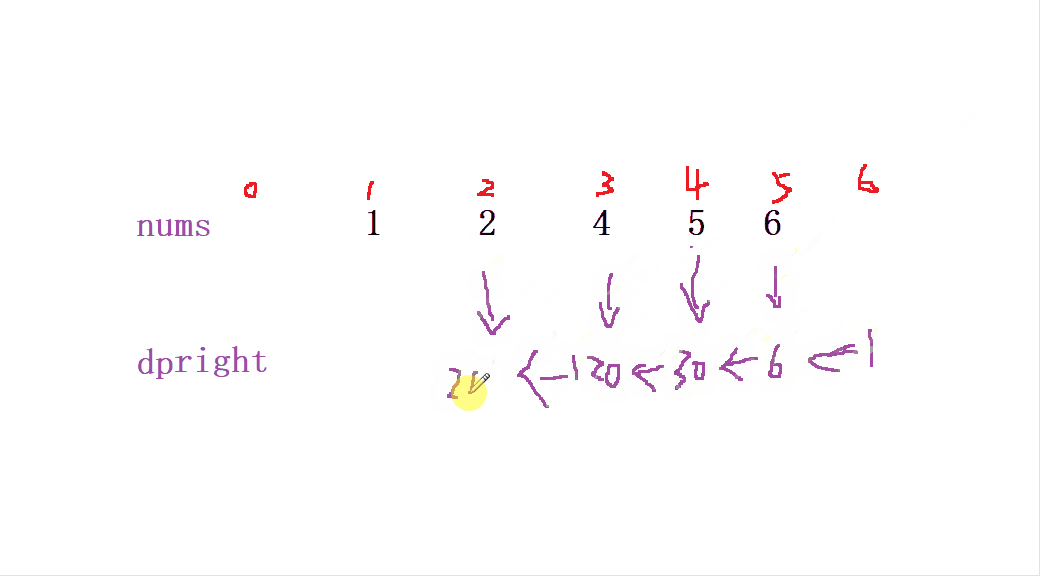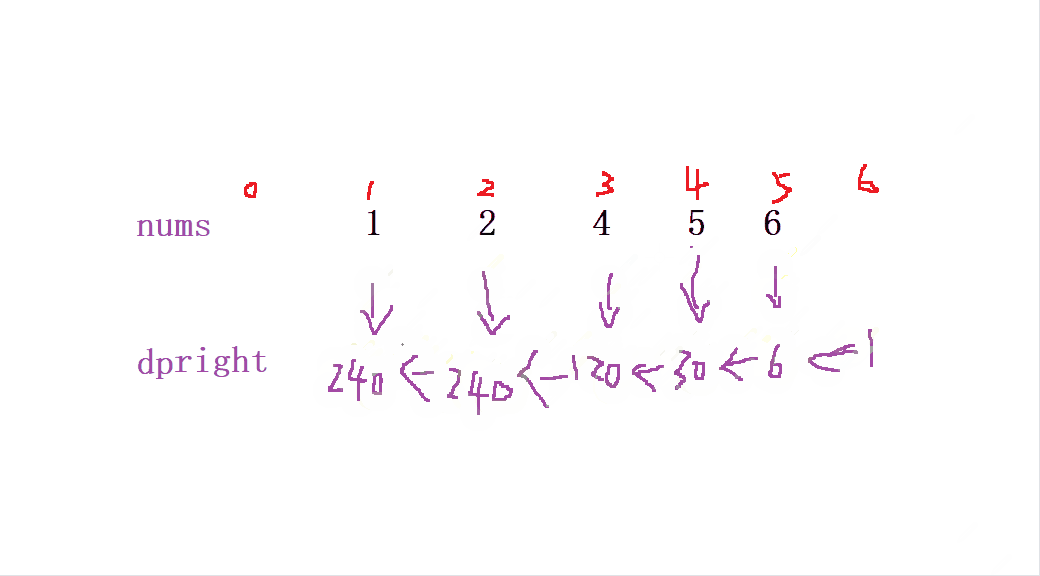
请添加图片描述

最后我们要获取到该位置的值就可以通过 ret[i]= dpleft[i] * dpright[i+1]; 来获取当前位置除自身以外的 乘积

<3>. 编写代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
         
        // 得到数组长度
        int n= nums.length;
    
        
        // 定义一个前缀积的数组
        int[] dpleft = new int [n+1];
        dpleft[0]= 1;

       // 进行前缀积
        for(int i =1 ; i < n+1 ; ++i) {
            dpleft[i]=nums[i-1] * dpleft[i-1];
        }  


        // 定义 一个后缀积的数组
        int[] dpright= new int[n+1];
        dpright[n]=1;

        // 进行后缀积的数组
        for(int  j = n-1 ; j >= 0; j-- ) {
            dpright[j]= nums[j] * dpright[j+1];
        }

        int[] ret= new int[n];

        // 得到返回值
        for(int i =0 ; i < n; ++i) {
            ret[i]= dpleft[i] * dpright[i+1];
        }


        return ret;
    }
}

在这里插入图片描述

鱼式疯言

本题的一点体会

本题的核心是如何写出 前缀积数组 和 后缀积的数组 的递推公式，以及边界值的处理细节

边界处理细节

  // 定义一个前缀积的数组
        int[] dpleft = new int [n+1];
        dpleft[0]= 1;
      // 定义 一个后缀积的数组
        int[] dpright= new int[n+1];
        dpright[n]=1;

定义一个比一个原来的数组的长度 +1 的 dp数组，并且把 最边界 都赋值为 1 (注意是 1，而不是为 0 )

2. 和可被 k 整除的子数组

974. 和可被 k 整除的子数组题目链接

<1>. 题目描述

在这里插入图片描述

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空）子数组的数目。

子数组是数组的连续部分。

示例 1：

输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

示例 2:

输入: nums = [5], k = 9
输出: 0

题目含义 ：

返回一段的所有能够被 k 整除 的 子数组 的个数

<2>. 讲解算法思想

解法一：

暴力枚举

解法二：

前缀和

讲解前缀和算法之前，我们先得熟悉 两个原理

1. 同余定理

如果 (a - b) % n == 0 ，那么我们可以得到一个结论： a % n == b % n 。

用文字叙述就是，如果两个数相减的差能被 n 整除，那么这两个数对 n 取模 的结果相同。

例如： ·(26 - 2) % 12 == 0 ，那么 26 % 12 == 2 % 12 == 2 。

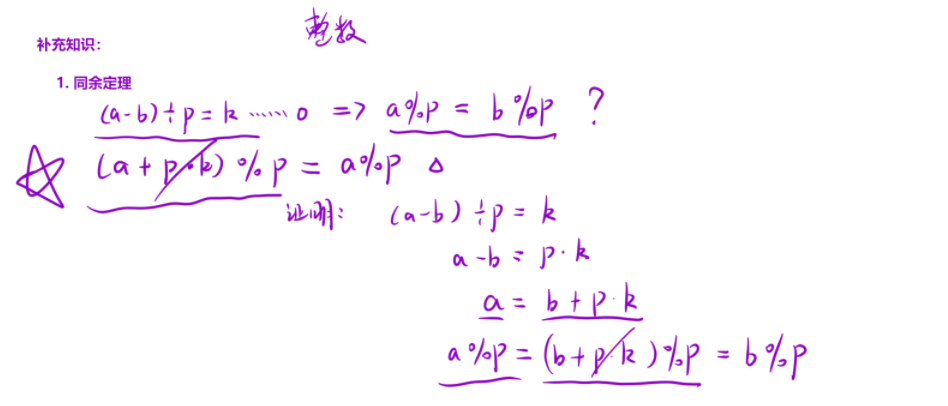
在这里插入图片描述

2. java 中负数取模的处理方法

a. Java 中关于负数的取模运算，结果是**「把负数当成正数，取模之后的结果加上一个负号」。**

例如： -1 % 3 = -(1 % 3) = -1

b. 因为有负数，为了防止发生「出现负数」的结果，以 (a % n + n) % n 的形式输出 保证为正 。

例如： -1 % 3 = (-1 % 3 + 3) % 3 = 2

在这里插入图片描述

前缀和算法步骤

设 i 为数组中的任意位置，用 sum[i] 表示 [0, i] 区间内所有元素的和。
想知道有多少个「以 i 为结尾的可被 k 整除的子数组」，就要找到有多少个起始位置为 x1, x2 , x3 … 使得 [x, i] 区间内的所有元素的和可被 k 整除。
设 [0, x - 1] 区间内所有元素之和等于 a ， [0, i] 区间内所有元素的和等于 b ，可得 (b - a) % k == 0 。
由 同余定理 可得， [0, x - 1] 区间与 [0, i] 区间内的前缀和同余。于是问题就变成：
找到在 [0, i - 1] 区间内，有多少前缀和的余数等于 sum [i] % k 的即可。

在这里插入图片描述

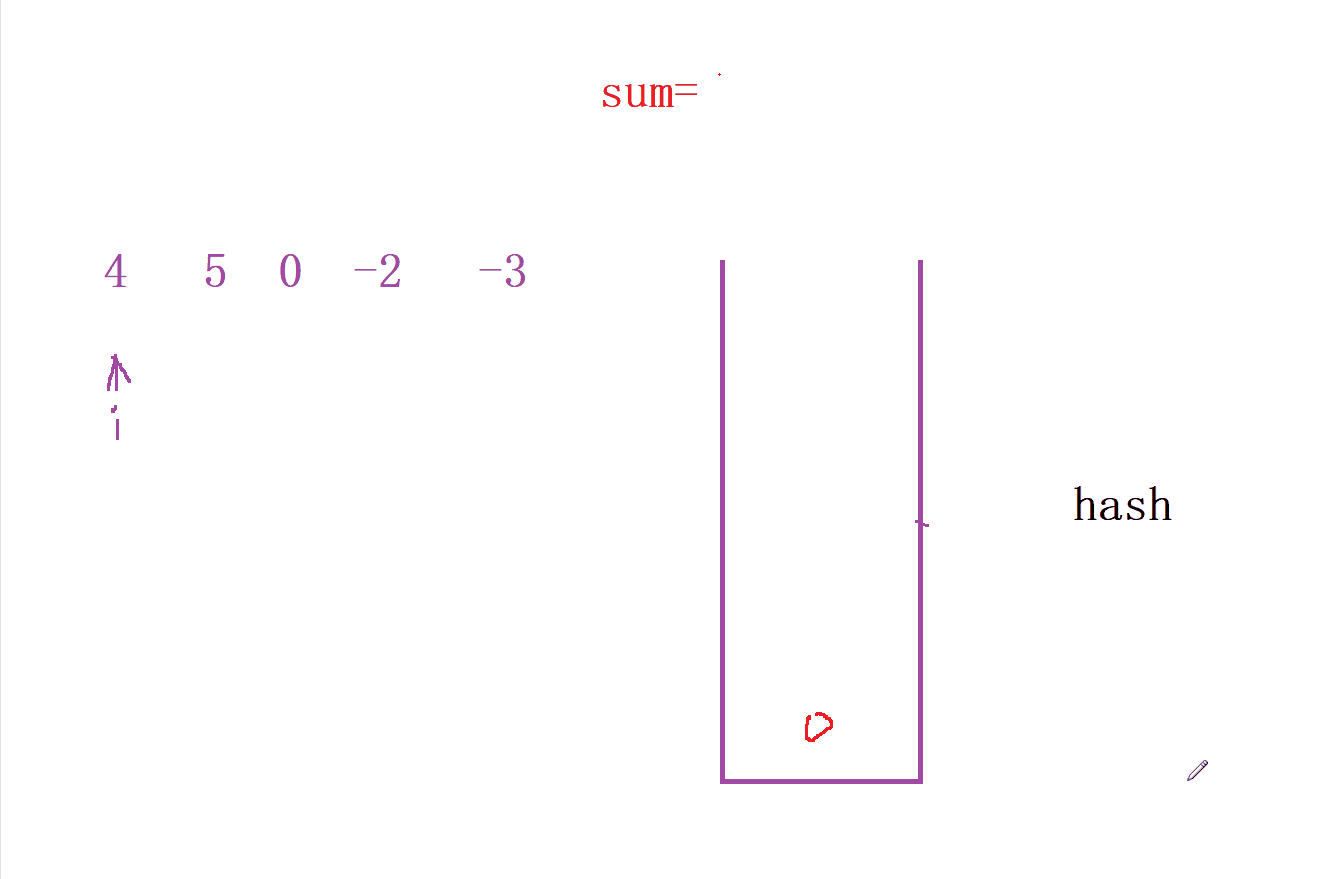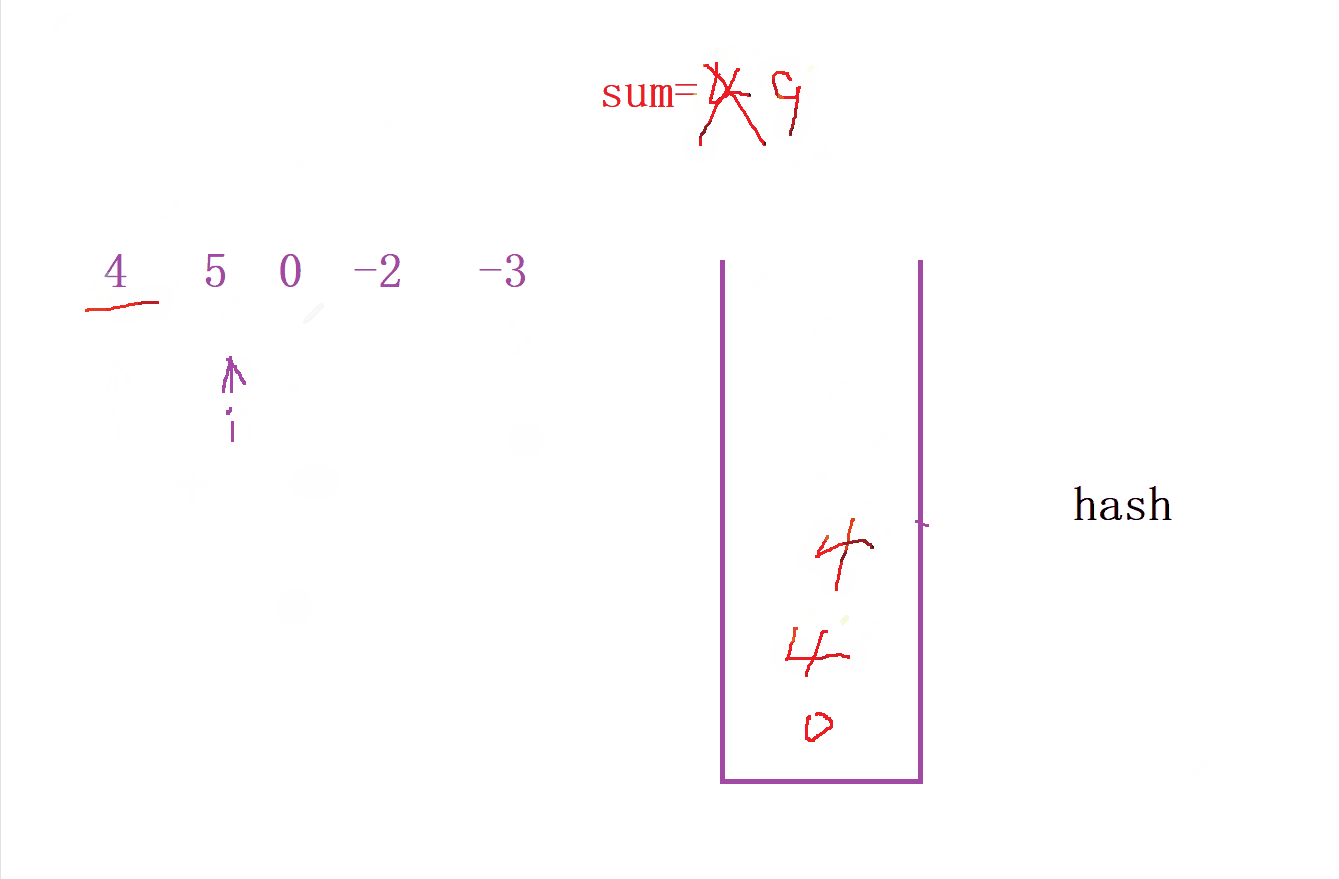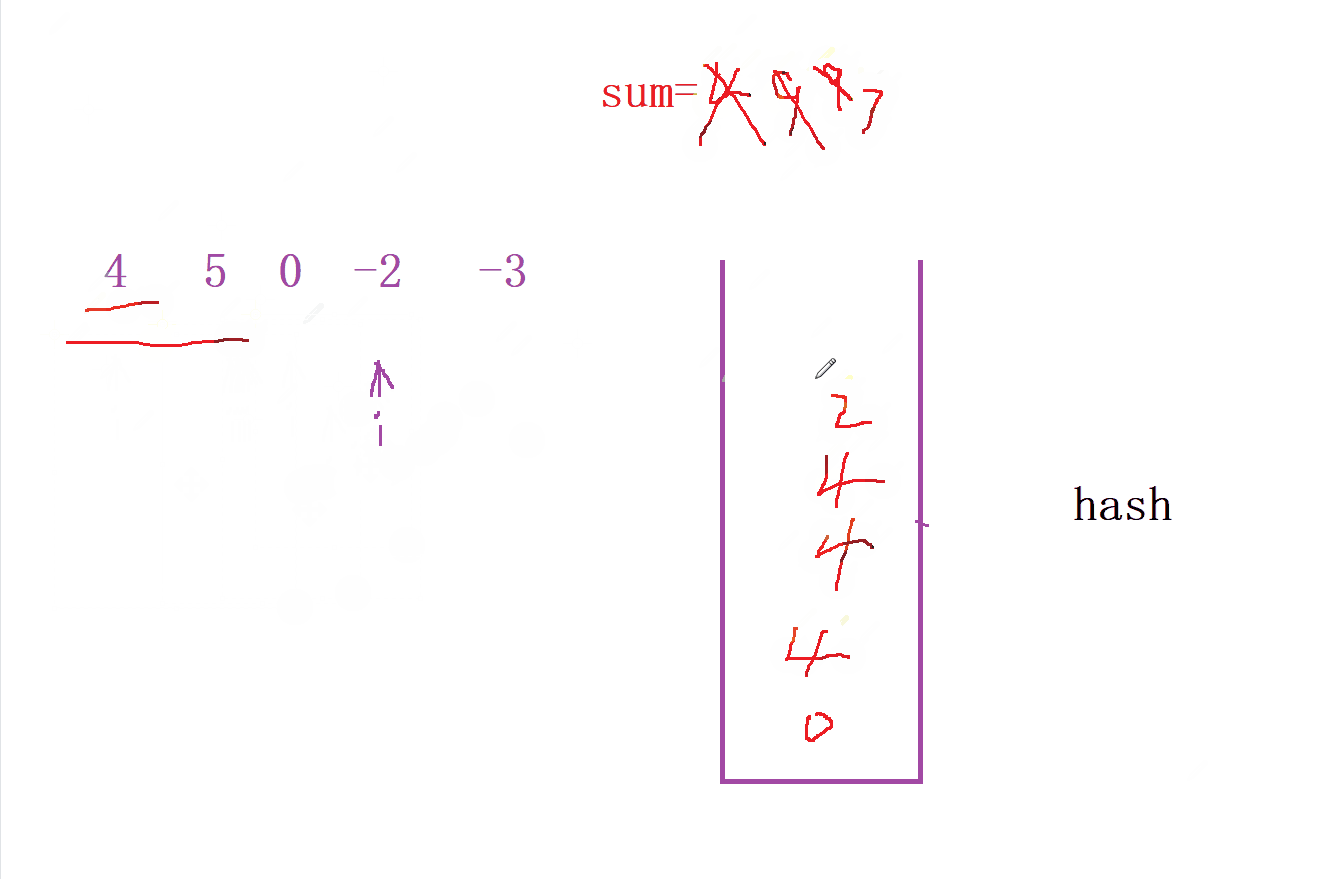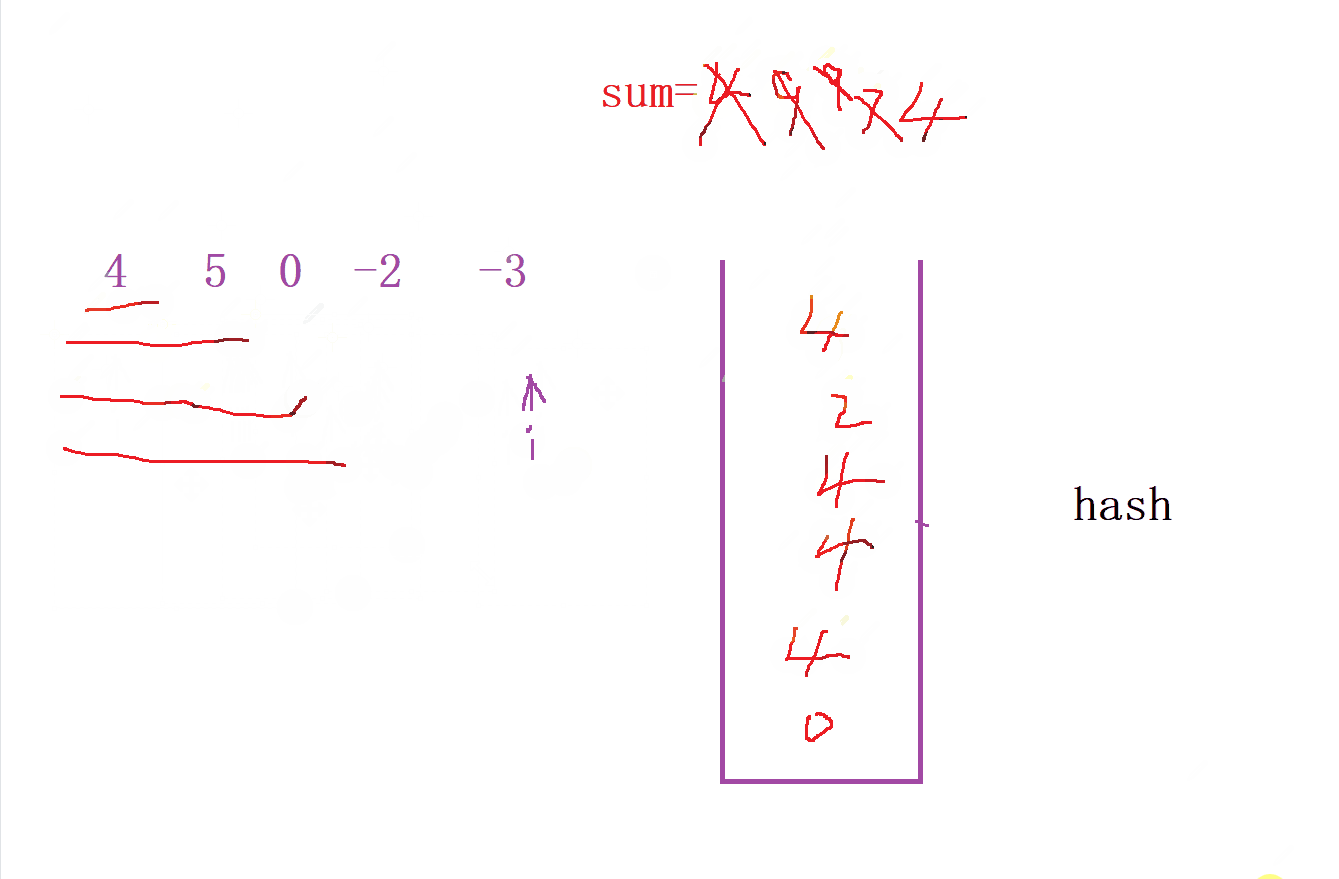
我们先定义一个 哈希表 来统计每次 前缀和的个数 ，并且寻找中间到是否前缀和中是否出现的 个数

然后我们就可以通过哈希表来寻找满足 sum[i] % k 的个数

请添加图片描述

<3>. 编写代码


class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        
        // 定义 一个哈希表
        Map<Integer, Integer> map= new HashMap<>();
        int n= nums.length;
        int ret=0,sum=0;

        // 可以理解为 从 0 位置放入 0 数据 
        map.put(0/k,1);


        for(int i=0; i < n; ++i ) {
            

            sum += nums[i];
            
            // 除去 Java 中 取模是 负数的情况
            int r=  (sum % k + k) % k  ;

            // 通过 余值定理 可知
            // sum % k =   a  % k
            // 这里就可以转化成 前面 【0, i-1】的位置 
            // 是否存在 哈希表中
            ret += map.getOrDefault(r,0);
            
            // 将前缀和数据放入 哈希表中
            map.put(r,map.getOrDefault(r,0)+1);
        }

        return ret;
    }
}

在这里插入图片描述

鱼式疯言

对于本题小编最大的体会

当我们需要求某个数的子数组时，借用 前缀和 和 哈希表 的结合来寻找前面的出现的 前缀和 来 查找是否满足 该数字的方法

   // 可以理解为 从 0 位置放入 0 数据 
        map.put(0/k,1);

细节处理

如果整段数值 前缀和为0 ，那么我们就需要制定一个默认值为 0 来进入哈希表

3. 连续数组

525.连续数组题目链接

<1>. 题目描述

在这里插入图片描述

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的 最长连续子数组，并返回该 子数组 的长度。

示例 1:

输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。

示例 2:

输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

题目含义 :

寻找一个 最长的连续子数组 0 和 1 个想等的长度

<2>. 讲解算法思想

题目分析

我们要 0 和 1 的个数想等，那么我们确定 0 和 1 的个数想等呢？

我们可以思考一下，如果把 0 改成 -1 ，只要 -1 和 1 相加为 0 不就 个数相等 了吗？ 🤔 🤔 🤔

算法步骤

从上一题的思路可得，我们的目的就是要寻找总和为 0 的一段子数组，我们就可以借助哈希表和前缀和。

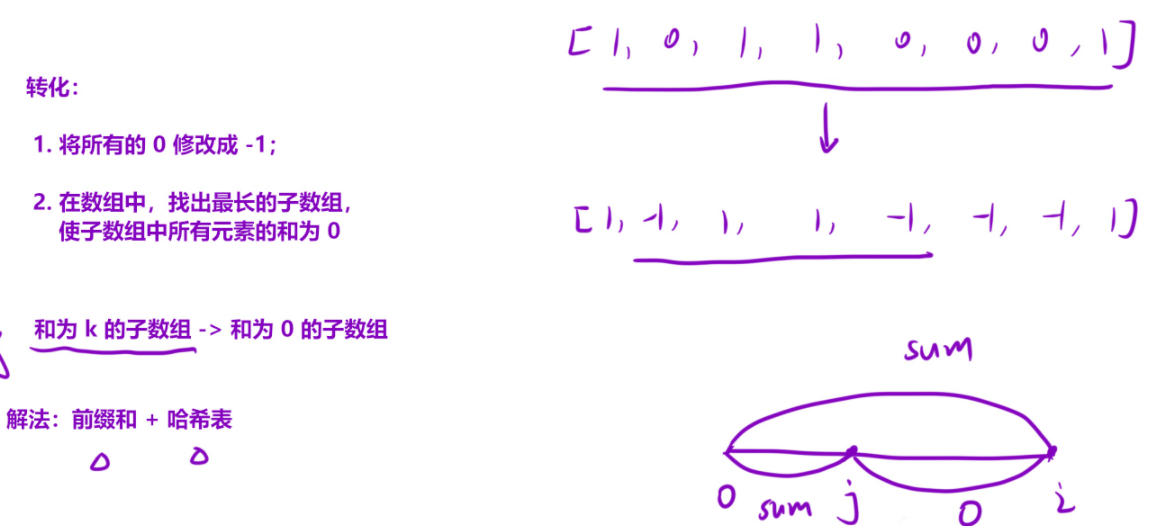
在这里插入图片描述

那么我们本质上还是寻找在现有的一段前缀和中去寻找一段区间是否等于 0 的个数

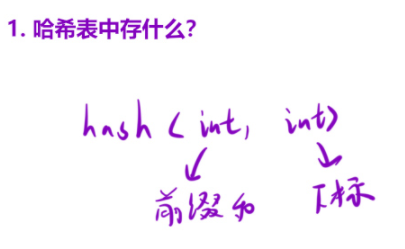
我们先定义一个 哈希表，因为我们要的长度，但这个哈希表统计的是当前位置的下标。

在这里插入图片描述

<3>. 编写代码

class Solution {
    public int findMaxLength(int[] nums) {

        int n= nums.length;
        // 定义个哈希表 
        // 左边为前缀和 ， 右边 为 下标位置
        Map<Integer , Integer> map= new HashMap<>();
        int len=0,sum = 0;
       


        map.put(0,-1);

        // 前缀和 + 哈希表
        for(int j=0; j < n ; j++) {

             // 进行前缀和   
            sum +=  (nums[j]==0 ? -1 : 1) ;
            

            // 这个本质上还是相当于 用 getOrdefault() 来判断

            // 更新结果
            if(map.containsKey(sum)) {

                len=Math.max(len,j - map.get(sum) );
            } else {
                // 如果不存在该前缀和 就 进行哈希表

                // 这里的细节就是 
                // 不需要进入重复元素
                map.put(sum,j);

            }
        }

        return len;

    }
}

在这里插入图片描述

鱼式疯言

对于本题小编最大的体会还是 0 转 -1 从而转化成总数为 0 这个思路

但核心还是我们的前缀和+哈希表来寻找我们一段子数组中和为 某个数 的方法

细节处理 ：

细节一 ：

   map.put(0,-1);

定义一个初始下标为 -1 ，方便我们计算数组的 长度，并处理 边界条件

// 更新结果
        if(map.containsKey(sum)) {

            len=Math.max(len,j - map.get(sum) );
        } else {
            // 如果不存在该前缀和 就 进行哈希表

            // 这里的细节就是 
            // 不需要进入重复元素
            map.put(sum,j);

        }

细节二 :

当该数字存在时，由于我们需要的数组的 最大长度，当出现下一个同样数字时， 左边的下标 的值就会 增大，从而导致 j - 左边下标值减小

数组长度减少 。

4.二维数组的前缀和

dp35. 二维数组的前缀和题目链接

<1>. 题目描述

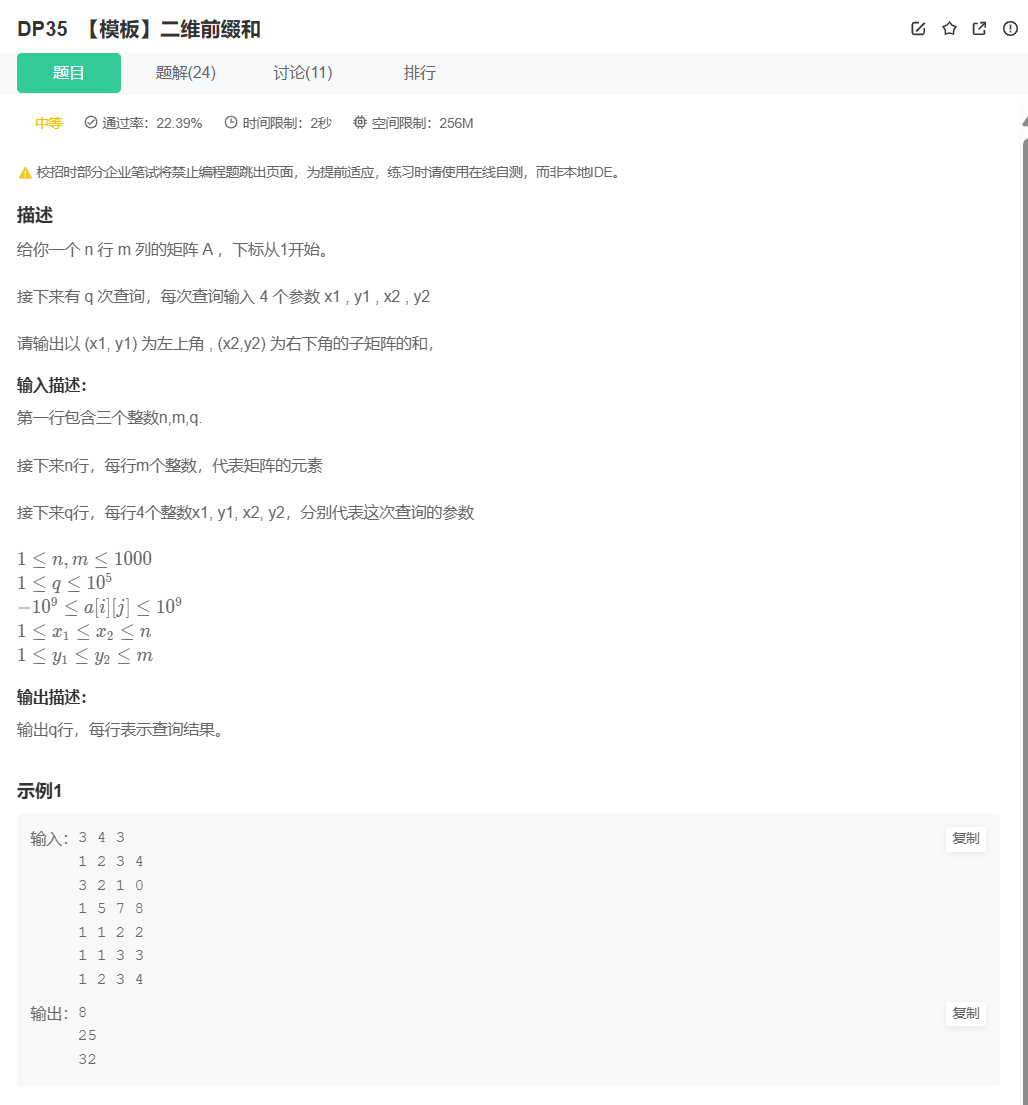
在这里插入图片描述

题目含义 ：

给定一个 左上角和右下角的坐标，求出左下角和右下角坐标所围成的矩阵的数字总和

<2>. 讲解算法思想

题目分析 ：

想要求本题，最好的思路还是利用我们的二维前缀和的思想

那么我们的 二维前缀和 该怎么计算？？？

提示一下：

我们需要在一维前缀和的基础上进行把二维数组进行拆分即可

算法步骤:

类比于一维数组的形式，如果我们能处理出来从 == [0, 0]== 位置到 == [i, j] == 位置这片区域内所有
元素的累加和，就可以在 O(1) 的时间内，搞定矩阵内任意区域内所有元素的 累加和 。因此我们
接下来仅需完成两步即可：

第一步：搞出来 前缀和矩阵

这里就要用到 一维数组 里面的拓展知识，我们要在矩阵的最上面和最左边添加上一行和一列 0，这样我们就可以省去非常多的边界条件的处理（同学们可以自行尝试直接搞出来前缀和矩阵，边界条件的处理会让你崩溃的）。处理后的矩阵就像这样：

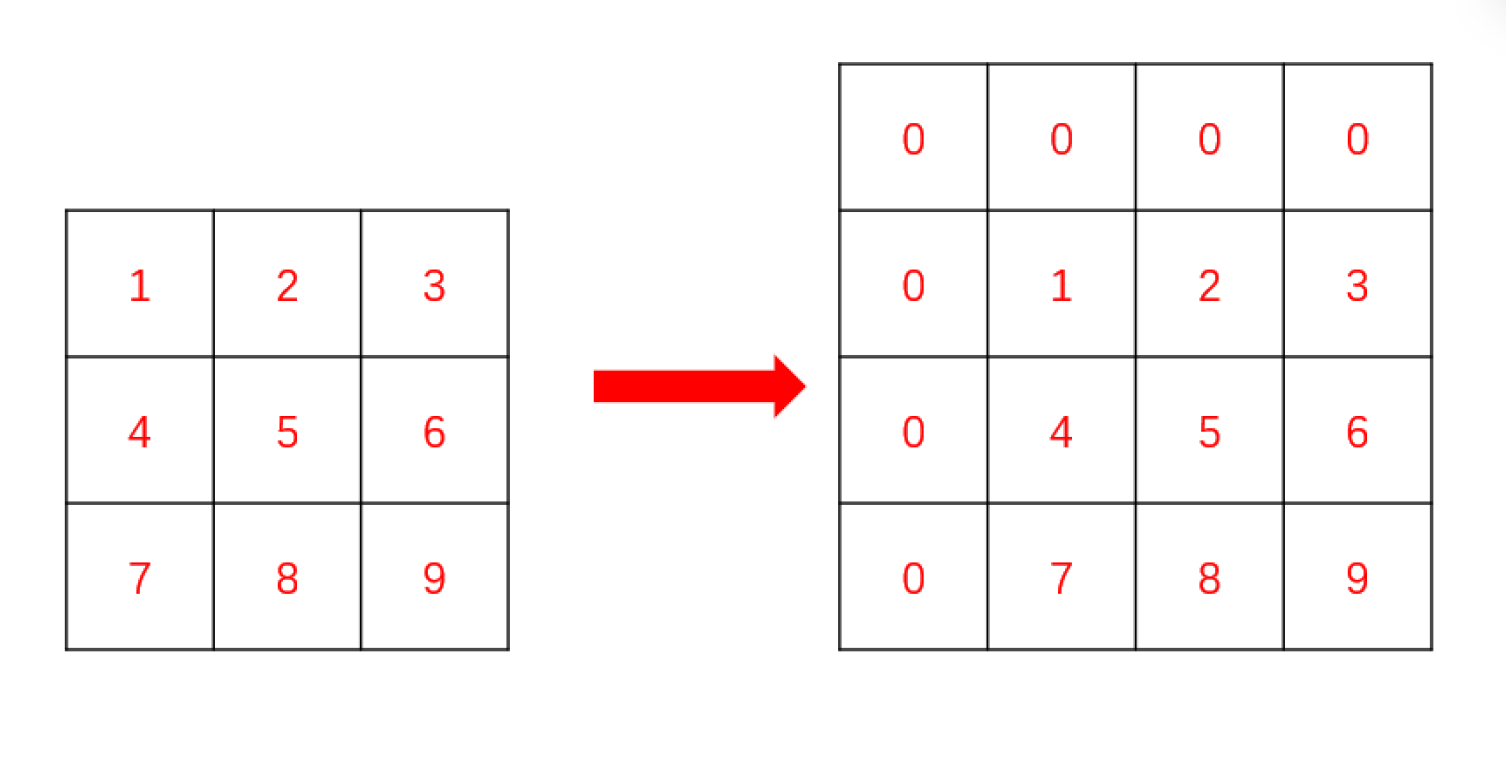
在这里插入图片描述

第二步

这样，我们填写前缀和矩阵数组的时候，下标直接从 1 开始，能大胆使用 i - 1 , j - 1 位
置的值。

注意 dp 表与原数组 matrix 内的元素的 映射关系：

i. 从 dp 表到 matrix 矩阵，横纵坐标减一；

ii. 从 matrix 矩阵到 dp 表，横纵坐标加一。

前缀和矩阵中 sum[i][j] 的含义，以及如何递推二维前缀和方程

sum[i][j] 的含义：

sum[i][j] 表示，从 [0, 0] 位置到 [i, j] 位置这段区域内，所有元素的累加和。对应
下图的红色区域：

简单来说就是：

如下图，假设红色区域为 a，紫色 区域为 b ，绿色区域为 d ， 橙色 区域为 c

计算前缀和时，我们就可以把他们看成是一块又一块的区域来累加

而我们通过这样的分解区域是需要得到 a + b + c + d 总和的面积，那我们就需要转化成 s= (a+b) + (a+c) + d - a 从而得到我们前缀和数组

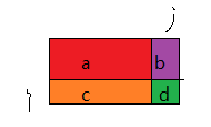
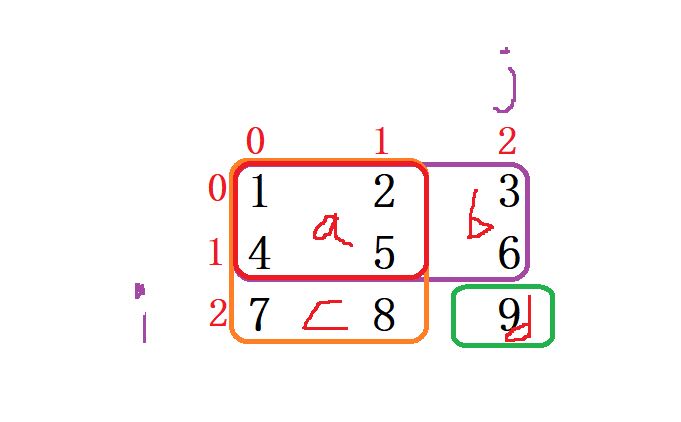
在这里插入图片描述

所以我们就可以推导出 dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + nums[i][j];

那么我们该怎么使用 二维前缀和数组 呢？

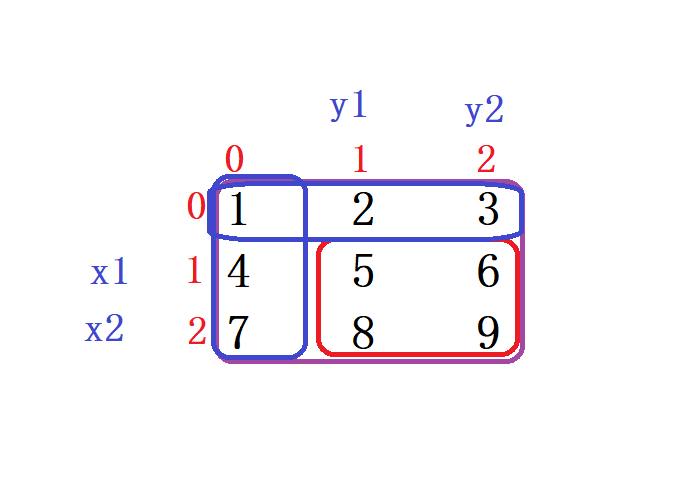
在这里插入图片描述

我们想要得到红色的区域，总得用 dp[x2][y2] - 区域 b - 区域 c + 区域 a 得到我们的区域 d

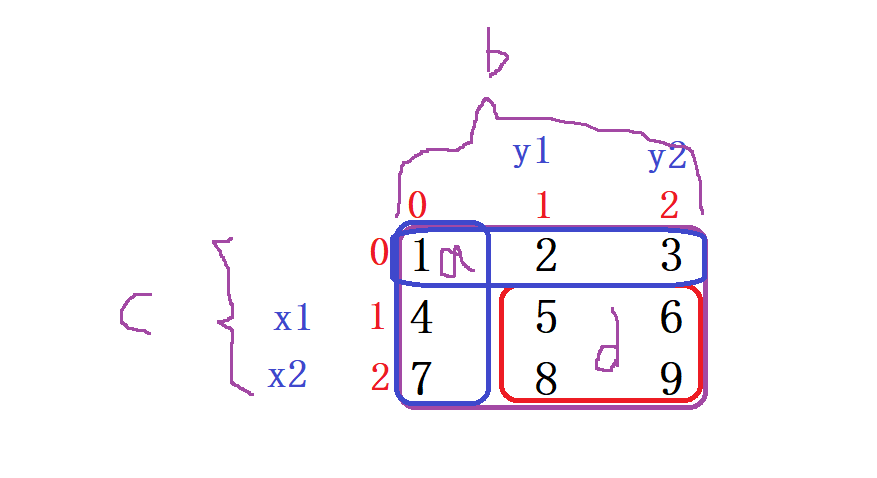
在这里插入图片描述

从中我们可以推导出使用二维前缀和的公式为： d = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];

<3>. 编写代码

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        int n = in.nextInt(), m = in.nextInt(), q = in.nextInt();
        long array[][] = new long[n + 1][m + 1];


        for (int i = 1; i < n + 1; ++i) {
            for (int j = 1; j < m + 1; j++) {
                array[i][j] = in.nextInt();
            }
        }

        long dp[][] = new long[n + 1][m + 1];
        for (int i = 1; i < n + 1; ++i) {
            for (int j = 1; j < m + 1; j++) {
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j] + array[i][j] - dp[i - 1][j - 1];
            }
        }


        while (q > 0) {
            int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();

            long sum = dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];


            System.out.println(sum);


            q--;
        }

    }
}

在这里插入图片描述

三.前缀和算法的总结

我们先初步认识了前缀和算法本质上就是 0到i 位置的和的一个数组，我们通过基本前缀和数组通过转化进行来实现对 子数组 的计算。
更在 ‘除自身以外的乘积’的上，我们认识到也可以同时构造 前缀和 以及 后缀和 的思想来实现对我数组 两头的同时计算
以及在 ‘和可被 k 整除的子数组’ 和 ‘连续数组’ 中，我们认识到可以用 前缀和 搭配 哈希表 来寻找某个固定值的子数组的 个数 或者 下标
最后的二维数组，更让我们在矩阵区域的思维上进行把二维数组进行划分成一段一段我们 已有的的区域 ，来 初始化和使用 我们的 二维前缀和数组