这道是洛谷官方题单的简单DP

为啥我放上来呢，因为我因为各种各样的细节原因没做出来

感觉计数的DP有点点难，得多写了

P4933 大师 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

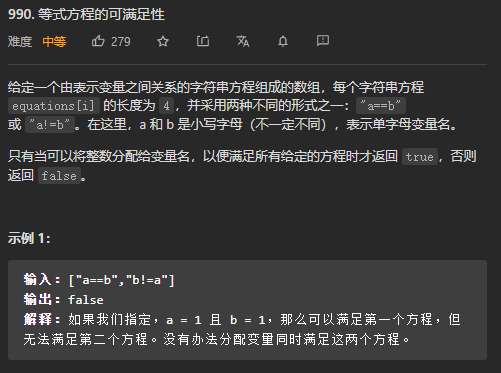
题意：

思路：

第一眼肯定是设dp[i][j]为以a[i]为结尾，公差为j的子序列的最大长度（子序列嘛，肯定是这样设的）

事实上这样是对的

但是我一开始一看数据范围，错误地判断数组开不下，于是去想了很多种DP状态设计，然后都失败了

二维数组的话，最多是能开到2e4*2e4的（亲测），所以不用担心

然后转移又是一个我不会想到的地方

我们去枚举前一个数的位置，因为两个数都确定了，因此不需要再去枚举公差

它是这样转移的：

dp[i][a[i]-a[j]+p]+=dp[j][a[i]-a[j]+p]+1;
dp[i][a[i]-a[j]+p]%=mod;

为什么要加一呢，要加上第i-1个和第i个这个子序列

这个点我根本想不到

还有一个细节就是：公差可能出现负数，这个处理方法就很典了：加上2e4就行了，注意把数组开大！

还有就是，单独一个数也算子序列，所以要加上

总之就是细节很多，非常容易做错QwQ

Code:

#include <bits/stdc++.h>
using namespace std;
const int mxn=1e3+10,mxv=4e4+10,mod=998244353;
int n,idx=0,ans=0,p=20000;
int a[mxn],dp[mxn][mxv];
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++){
        ans++;
        for(int j=1;j<i;j++){
            dp[i][a[i]-a[j]+p]+=dp[j][a[i]-a[j]+p]+1;
            dp[i][a[i]-a[j]+p]%=mod;
            ans+=dp[j][a[i]-a[j]+p]+1;
            ans%=mod;
        }
    }
    cout<<ans<<'\n';
}