前言：

---

注：代码随想录中没有很清楚的提起想出方法的思路，只是给出了解决这个问题的大致思路和代码；下面我将介绍一下我的思考过程，并贴出实现代码；

---

a

a

a

a

思考过程：

---

思路1：为了可以直观理解，我们将评分数组ratings画成折线图，并举几个样例加深理解

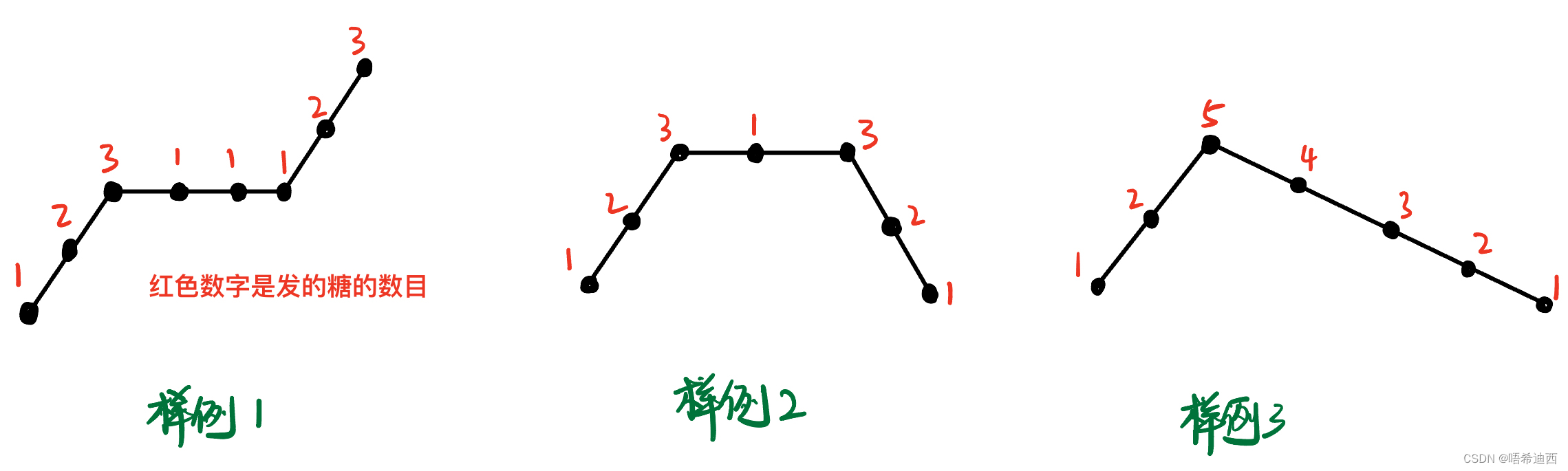
注意1：我们可以发现，如果出现一段评分相同的情况，那么评分相同这一段的中间那些节点可以无脑选择赋值为1；

注意2：对于峰值的赋值，如样例3，需要找到离这个波峰最近的两个波谷，从1开始加直到这个波峰，最终比较谁的值大就选谁，因为每个孩子最少一个糖，所以我们要保证波峰沿着最长的路径下降时，下降到最底下还有1来兜底；

a

a

思路2：所以我们的思路转变为如何通过评分数组 ratings 来得到所有的波峰和波谷？

• 知道波谷的位置，我们才知道哪些位置应该直接赋值为1，即所有的波谷可以无脑赋值为1；
• 知道波峰的位置，我们才能通过波峰的位置，找到该波峰左右两边各一个离这个波峰最近的波谷的位置，然后对比两个波谷谁离波峰最远，就选哪个开始一路上升（+1）来给波峰赋值；即样例3表示的情况；

a

a

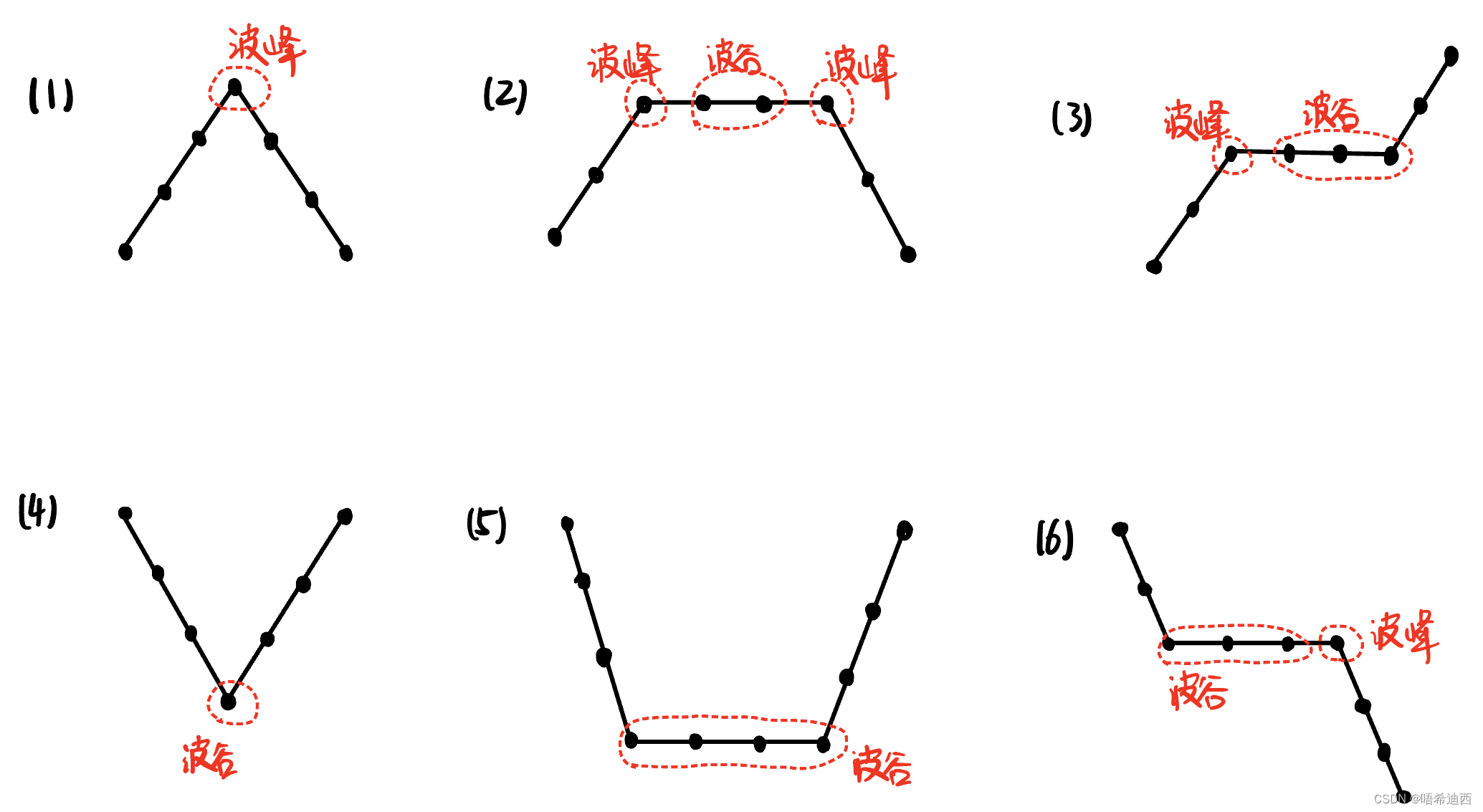
思路3：所有的折线情况一共有6种，我们判断这6种情况中哪些位置是波峰，哪些位置是波谷？

注意：元素类型分为三类（图中未给出类型的元素即为第3类元素）

• 波峰
• 波谷
• 既不是波峰，也不是波谷

a

a

思路4：如果我们按照上面的6种情况来写我们的代码，先不说还要考虑开头和结尾的特殊情况，就堪堪这六种情况，我tm都想把键盘砸了；所以不可能从头到尾遍历ratings中所有的元素一次，就可以将每个元素的类别（波峰 / 波谷 / 既不是峰也不是谷）给分清楚；

思路5：所以我们另辟蹊径，还是根据我最上面提供的样例3，如果想给波峰赋值，我们需要在两个方向的波谷同时往波峰出发，对波峰赋值，所以我们可不可以？先走【波谷 --> 波峰】这条路，给波峰赋值；再走【波峰 <--  波谷】对波峰赋值；然后选择最大的那个值作为波峰真正的值？

思路6：那么我们可以将遍历一次改成遍历两次数组ratings，第一次遍历为【从左往右】，第二次遍历为【从右往左】，然后记录两次遍历的值，选择最大的值为该节点的值；

注意：不止是波峰可以这样处理，所有的节点都是这样的处理流程；

---

a

a

a

a

代码实现：

---

class Solution {
public:
    int candy(vector<int>& ratings) {
        //自己尝试：贪心算法
        vector<int> result(ratings.size(), 1);

        //正向遍历：
        for(int i = 1; i < ratings.size(); i++) {
            if(ratings[i] > ratings[i - 1]) result[i] = result[i - 1] + 1;
        }

        //反向遍历：
        for(int i = ratings.size() - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]) result[i] = max(result[i + 1] + 1, result[i]);
        }

        //求总和：
        int sum = 0;
        for(int i = 0; i < result.size(); i++) {
            sum += result[i];
        }

        return sum;
    }
};

---