一:打包

1.打包前的分析

文件路径下+npm run preview -- --report

生成打包之后的内容

2.解决有些内容体积过大的问题

1.删除有些不使用但是占用较多的,将main.js上import删除,打包时不会有

2.不能删除但是内容较大的

vue.config.js文件夹下

 externals: {
      'vue': 'Vue',
      'element-ui': 'ELEMENT',
      'cos-js-sdk-v5': 'COS'
    }
可以即使有import也不去导入,而且对于之前导入的部分当运行时查找Vue全局变量

 <script src="https://lf9-cdn-tos.bytecdntp.com/cdn/expire-1-M/vue/2.6.14/vue.min.js"></script>
    <script src="https://cdn.bootcdn.net/ajax/libs/element-ui/2.15.13/index.min.js"></script>
    <script src="https://cdn.jsdelivr.net/npm/cos-js-sdk-v5/dist/cos-js-sdk-v5.min.js" ></script>

script不会被打包,但是等运行会执行导入,上述的外部也会查找导入的全局变量,进行操作.因此打包体积缩小,但是运行查找cdn的文件,导入,一样的.内存里仍然有.

 <link href="https://cdn.bootcdn.net/ajax/libs/element-ui/2.15.13/theme-chalk/index.min.css" rel="stylesheet">
  <link href="https://cdn.bootcdn.net/ajax/libs/element-ui/2.15.13/theme-chalk/index.min.css" rel="stylesheet">
打包不导入,但是放到这里,执行的时候运行导入index.html下

二:打包

进行前述打包分析,对大的文件进行处理之后,我们就进行打包

三:服务器内运行访问

1.mac电脑

1)下载nginx服务器

安装nginx

brew install nginx  

查看版本

brew info nginx #查看nginx

2)将生成的dist下的文件复制拷贝到html文件夹下

3)开启服务器

服务器安装但是默认是关闭的,只有开启,才能在网站内找到,执行

brew info nginx #查看nginx
查看地址  

/opt/homebrew/Cellar/nginx/1.23.3/bin/nginx #启动命令

 /opt/homebrew/Cellar/nginx/1.23.3/bin/nginx -s stop  #停止命令

可以在任意路径下执行

务器需要知道静态文件所在的目录，以便能够正确地响应客户端的请求。之后放也不会有地址.

4)访问

 1.使用hisory模式

     

使得网站地址是不带#,地址变化重新刷新.#仍能访问到.反之不可,#用来分辨那个是那一部分.history会忽视#.

2)访问的时候,http://域名+8080端口名(固定)+地址.

http://localhost/8080/#/login原本会根据路由来访问对应的.

但是打包之后默认后面的是html文件,访问服务器下login.html文件,再根据地址访问路由对应的内容.

mac-配置文件路-/opt/homebrew/etc/nginx/nginx.conf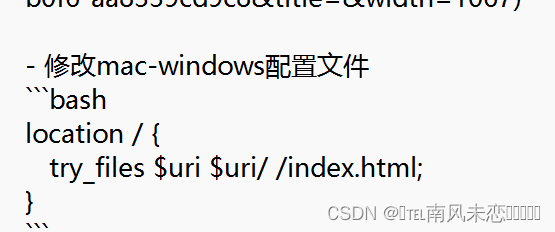 

$ /opt/homebrew/Cellar/nginx/1.23.3/bin/nginx -s reload  #重启
不重启,服务器访问不会有效

2.window电脑

1)下载nginx服务器

1. 打开 Nginx 的官方网站：https://nginx.org/。
2. 在网站的首页上方，你会看到一个下载按钮。点击该按钮将会跳转到下载页面。
3. 在下载页面中，你会看到列出了不同版本的 Nginx。找到适合你的 Windows 系统的稳定版本。
4. 在 Windows 系统下，你可以选择下载预编译的二进制文件。根据你的系统架构（32位或64位），选择相应的版本进行下载。
5. 点击下载链接，将会开始下载 Nginx 的压缩文件（通常是一个 zip 文件）。
6. 下载完成后，解压缩压缩文件到你想要安装 Nginx 的目录。

2)将生成的dist下的文件复制拷贝到html文件夹下

3)启动服务器

点击.exe文件即可启动

找到下载的文件夹的路径执行$./nginx -s stop  #停止命令

4)使得只指向一个index.html文件和mac一样

但是都需要重启

$ ./nginx -s reload  #重启
四:生产环境跨越

只要修改了配置文件就需要重启否则无效的.

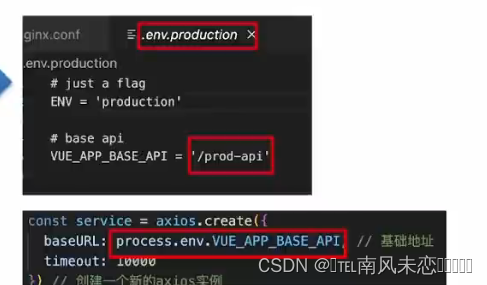
这里会使得生产模式和开发模式的地址不同.

在下面的配置当中使得访问服务器.

```bash
location /prod-api  {
  proxy_pass https://heimahr-t.itheima.net;(需要加分号,需要请求的地址)
}
 

上述实现请求.

重启是在nginx文件夹下

二:vuex仓库