导语

leetcode刷题笔记记录，本篇博客记录数组基础1部分的题目，主要题目包括：

• 977.有序数组的平方 ，
• 209.长度最小的子数组 ，
• 59.螺旋矩阵II

知识点

滑动窗口

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。一般需要用到双指针来进行求解。

模拟

模拟并不涉及到什么算法，就是模拟过程，但却十分考察对代码的掌控能力。 需要对边界值和循环过程进行仔细的考虑。

Leetcode 977 有序数组的平方

题目描述

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入： nums = [-4,-1,0,3,10]
输出： [0,1,9,16,100]
解释： 平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入： nums = [-7,-3,2,3,11]
输出： [4,9,9,49,121]

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 已按 非递减顺序 排序

进阶：

• 请你设计时间复杂度为 O(n) 的算法解决本问题

解法

可以使用双指针，从两边往中间走，这样会得到一个从大到小排列的数组，返回结果时只需要倒置一下就可以了。

class Solution(object):
    def sortedSquares(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        left, right = 0, len(nums) - 1
        ans_l = []
        while left <= right:
            if abs(nums[left]) >= abs(nums[right]):
                ans_l.append(nums[left] ** 2)
                left += 1
            else:
                ans_l.append(nums[right] ** 2)
                right -= 1
        return ans_l[::-1]

同时，也可以令双指针从中间开始（即从正负数分界处开始），为此，需要先找到正负数的分界线，代码如下：

class Solution(object):
    def sortedSquares(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        # 寻找分割点
        cut = -1
        for num in nums:
            if num < 0:
                cut += 1
            else:
                break
        # 这样cut右边都是非负数，左边都是负数
        left, right = cut, cut + 1
        ans_l = []
        while left>= 0 or right <= len(nums)-1:
            if left < 0:
                ans_l.append(nums[right] ** 2)
                right += 1
            elif right > len(nums) - 1:
                ans_l.append(nums[left] ** 2)
                left -= 1
            elif -nums[left] <= nums[right]:
                ans_l.append(nums[left] ** 2)
                left -= 1
            else:
                ans_l.append(nums[right] ** 2)
                right += 1

        return ans_l

Leetcode 209 长度最小的子数组

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ****≥ target ****的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度 。 如果不存在符合条件的子数组，返回 0 。

示例 1：

输入： target = 7, nums = [2,3,1,2,4,3]
输出： 2
解释： 子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入： target = 4, nums = [1,4,4]
输出： 1

示例 3：

输入： target = 11, nums = [1,1,1,1,1,1,1,1]
输出： 0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

解法

最简单的解法为暴力解法，但Leetcode上已经提示，Python的暴力解法一定会超时，所以这里使用滑动窗口来解决这个问题。

暴力解法中一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，那么滑动窗口如何用一个for循环来完成这个操作呢。

一个最关键的问题在于如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置？如果只用一个for循环来表示滑动窗口的起始位置，那么如何遍历剩下的终止位置？此时难免再次陷入暴力解法的怪圈。所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。

滑动窗口解法

class Solution(object):
    def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        start, ans = 0, 0
        min_length = len(nums) + 1
        for end in range(len(nums)):
            ans += nums[end]
            while ans >= target:
                min_length = min(end-start+1, min_length)
                ans -= nums[start]
                start += 1
            
        return min_length if min_length <= len(nums) else 0

Leetcode 59 螺旋矩阵II

题目描述

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

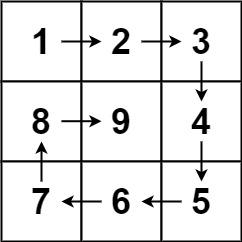
输入： n = 3
输出： [[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入： n = 1
输出： [[1]]

提示：

• 1 <= n <= 20

解法

这个题目的过程就是模拟，需要考虑好边界值条件，一个解题的关键是处理好区间选取，为了代码统一和边界值统一考虑，应选取左开右闭的区间，即每一行列都只考虑起始位置点，而不考虑终止位置点。

代码如下：

class Solution(object):
    def generateMatrix(self, n):
        """
        :type n: int
        :rtype: List[List[int]]
        """
        matrix = [[0] * n for j in range(n)]
        cnt = 1
        offset = 1
        start_x, start_y =0, 0
        loop = n // 2
        
        while loop:
            for j in range( start_y, n - offset ):
                matrix[start_x][j] = cnt
                cnt += 1
            for i in range( start_x, n - offset ):
                matrix[i][n-offset] = cnt
                cnt += 1
            for j in range( n - offset, start_y, -1):
                matrix[n-offset][j] = cnt
                cnt += 1
            for i in range( n - offset, start_x, -1):
                matrix[i][start_y] = cnt
                cnt += 1
            start_x += 1
            start_y += 1
            offset += 1
            loop -= 1

        if n%2 == 1:
            matrix[n//2][n//2] = n * n 

        return matrix

参考

• 代码随想录
• 题解