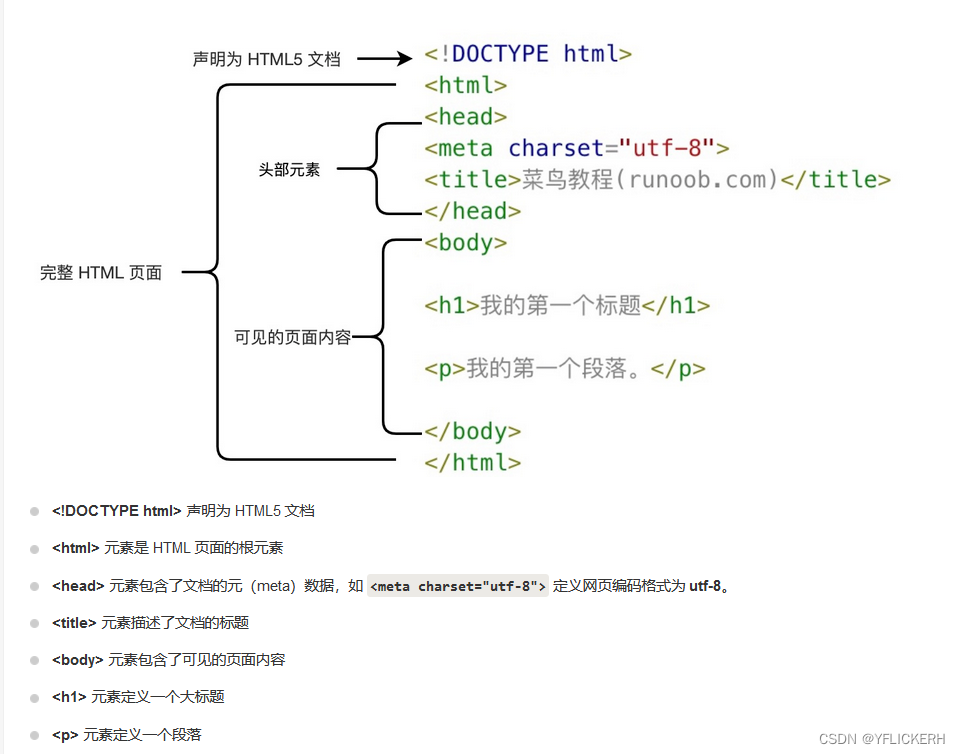
文章目录
- 数据归一化的使用
- 最值归一化
- 均值方差归一化(常用)
- 在sklearn中调用归一化(鸢尾花数据归一化)
数据归一化的使用
为什么要使用数据归一化?
举个例子,例如我们要使用KNN算法来预测肿瘤为良性肿瘤或恶性肿瘤。以下是一些数据:
| 肿瘤大小(厘米) | 发现时间(天) | 肿瘤类型 | |
|---|---|---|---|
| 样本1 | 1 | 200 | 良性肿瘤 |
| 样本2 | 5 | 100 | 恶性肿瘤 |
| 样本3 | 2 | 150 | 良性肿瘤 |
根据以上数据,画出散点图
import numpy as np
import matplotlib.pyplot as plt
# 训练集数据
X_train = np.array([
[1, 200],
[5, 100],
[2, 150]
])
y_train = np.array([1,0,1]) # 1为良性,0为恶性
# 绘制散点图
plt.figure(dpi=100)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1,1], color='b') # 蓝色为良性
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0,1], color='r')
plt.xlabel("肿瘤大小(厘米)")
plt.ylabel("发现时间(天)")
plt.legend(loc="best")
plt.show()
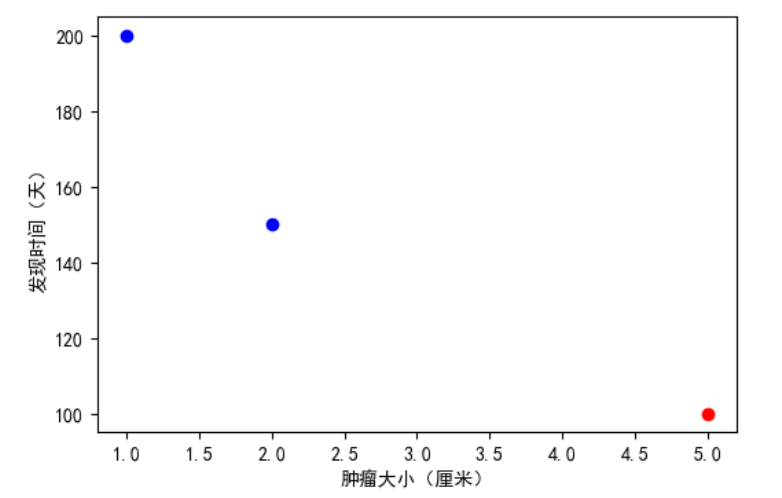
观察上图,并未发现任何问题。当我们计算样本1和样本2的距离时,公式为:
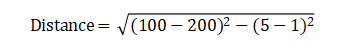
我们可发现纵坐标的数据远远大于横坐标的数据。这样在我们进行计算时,由于发现时间的影响远大于肿瘤大小的影响,所以预测相当于只采用了一个特征。
因此我们需要进行数据归一化
最值归一化
最值归一化:把所有数据映射到0-1之间。公式如下:

以上述例子为例:对发现时间的特征进行最值归一化。
import numpy as np
X = np.array([
[1, 200],
[5, 100],
[2, 150]
])
X = np.array(X, dtype='float')
X[:,1] = (X[:,1]-np.min(X[:,1]))/(np.max(X[:,1])-np.min(X[:,1]))

均值方差归一化(常用)
均值方差归一化:它是把所有数据归到均值为0,方差为1的分布中。即确保最终得到的数据均值为0,方差为1。公式如下:
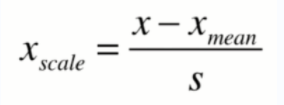
以上述例子为例:对发现时间的特征进行均值方差归一化。
import numpy as np
X = np.array([
[1, 200],
[5, 100],
[2, 150]
])
X = np.array(X, dtype='float')
X[:,1] = (X[:,1]-np.mean(X[:,1]))/np.std(X[:,1]) #np.std()--求方差
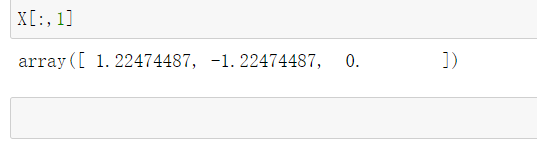
在sklearn中调用归一化(鸢尾花数据归一化)
- 导入模块
import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler # 均值方差归一化
from sklearn.model_selection import train_test_split
- 获取数据并预处理
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
std_scaler = StandardScaler()
std_scaler.fit(X_train) # 计算均值和方差
X_std_train = std_scaler.transform(X_train) # 对训练集特征进行归一化处理
X_std_test = std_scaler.transform(X_test) # 对测试集特征进行归一化处理

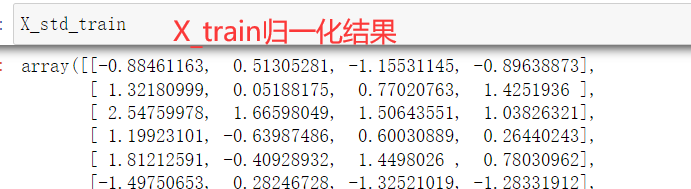
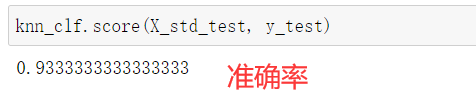
- 调用sklearn中的KNN算法,计算出准确率
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_std_train, y_train)
knn_clf.score(X_std_test, y_test)