前言
声明:本文所有动图来源为菜鸟教程
🍀作者简介:被吉师散养、喜欢前端、学过后端、练过CTF、玩过DOS、不喜欢java的不知名学生。
🍁个人主页:红中
🍂不就是蓝桥杯嘛,干他!!我堂堂
上一期说完了三种简单排序,这一期来说说三种高级排序方法
分别是
- 快速排序
- 希尔排序
- 归并排序
1、快速排序
这个排序方法说起来和冒泡排序有点像,为什么这么说呢,咱先来看图

相对于上一期的简单排序而言,高级排序肯定就不是能一眼看出来了
不说废话了
这玩意分两步
第一步,快速排序首先需要的东西,是一个枢轴值,也就是基准
怎么说?
实际上就是,我选出来一个数作为基准
然后进行分割:比这个基准大的放在该基准的右边,比这个基准小的放在该基准的左边,和基准一样大的,放左右都行
第二步,将基准左/右侧的子序列进行递归排序
实例
def QuickSort(arr):
if(len(arr)<2): #不用进行排序
return arr
else:
pivot=arr[0]
less=[i for i in arr[1:] if(i<=pivot)]
great=[i for i in arr[1:] if(i>pivot)]
return QuickSort(less)+[pivot]+QuickSort(great)
arr=list(map(int,input().split(' ')))
print("原始数据:",arr)
print("排序后的数据:",QuickSort(arr))那么这里,我们并没有完全采用上述原理
而是使用重复二分的方式,将数据分为更大与更小两个列表
通过更小+基准+更大
重复拼接,来达到目的
首先来进行读取数据
然后调用函数,如果列表里只有一个元素或者没有元素,就不需要判断
否则,以第一个元素作为基准,分出比他大的和比他小的,分别放在两个列表中,进行拼接
吉师大一python算法第二天(1)
2、希尔排序
希尔排序其实不难,说白了就是插入排序plus,咱们可以很容易地理解
这个排序算法主要利用到了步长
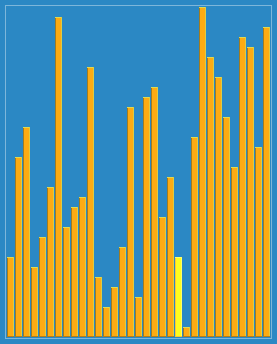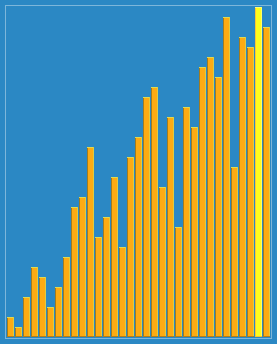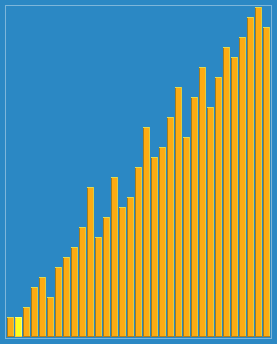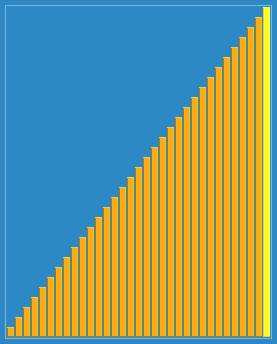
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
接下来直接看实例,并讲解
实例
nums = list(map(int,input().split(' ')))
def ShellSort(nums):
step = len(nums)//2 #初始化增量为数组长度的一半
while step > 0: #增量必须是大于0的整数
for i in range(step,len(nums)):#遍历需要进行插入排序的数
while i >= step and nums[i] < nums[i-step]: #对每组进行插入排序
nums[i],nums[i-step] = nums[i-step],nums[i]
step //= 2#增量缩小一半
print(nums)
ShellSort(nums)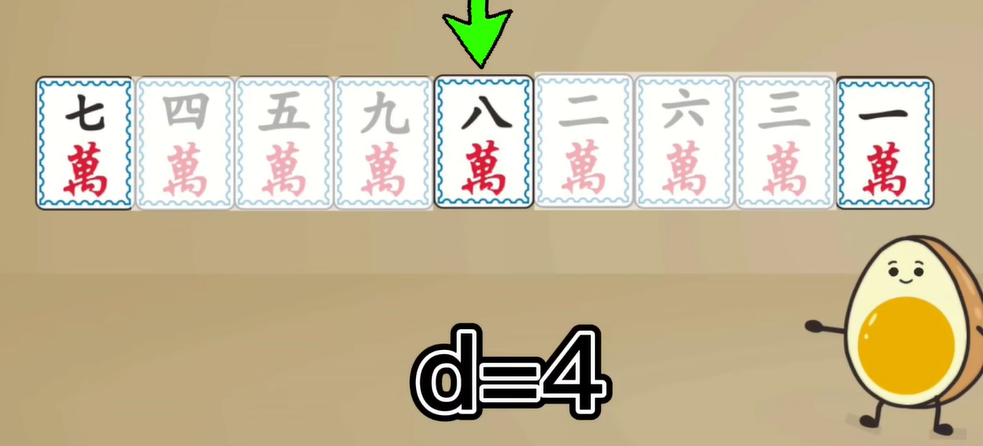
上图原地址 :秒懂算法3-希尔排序_哔哩哔哩_bilibili
按上图来解释,首先我们去步长/跨度
用列表整体长度整除2,上图中一共有九张牌,9//2就等于4,由于我们的循环是从step,也就是第四位开始的,所以我们要判断的条件是八万是否要小于七万。
不小于,不执行
i递增,到了二万,她所对应的是四万,小于,即换位
以此类推到最后一位
结束循环,后缩小步长,再来一遍,直到步长为一,整体排一遍
3、归并排序
基本思想:
- 分割:递归地把当前序列平均分割成两半
- 集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)
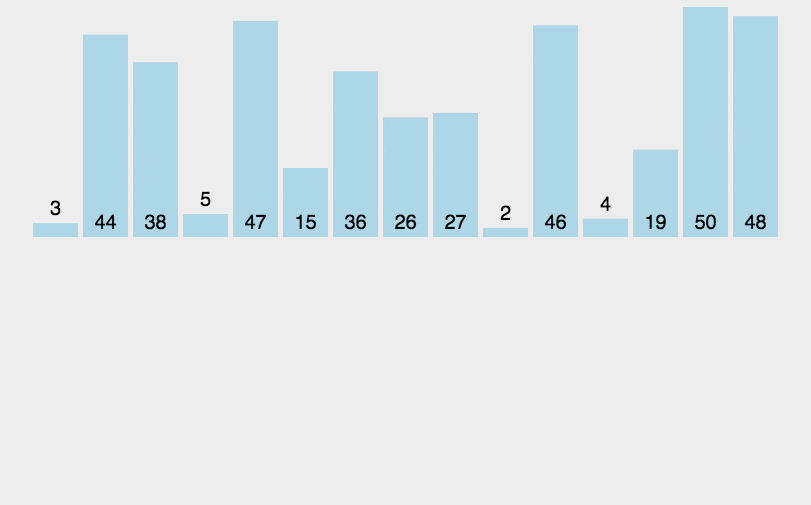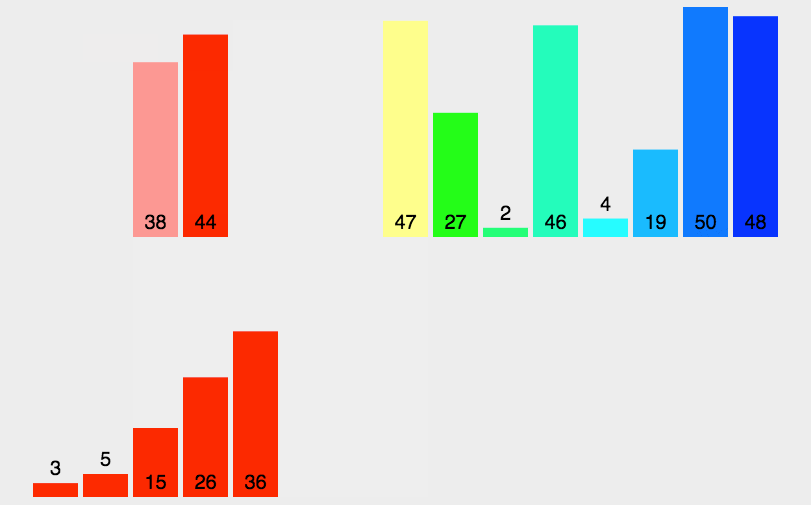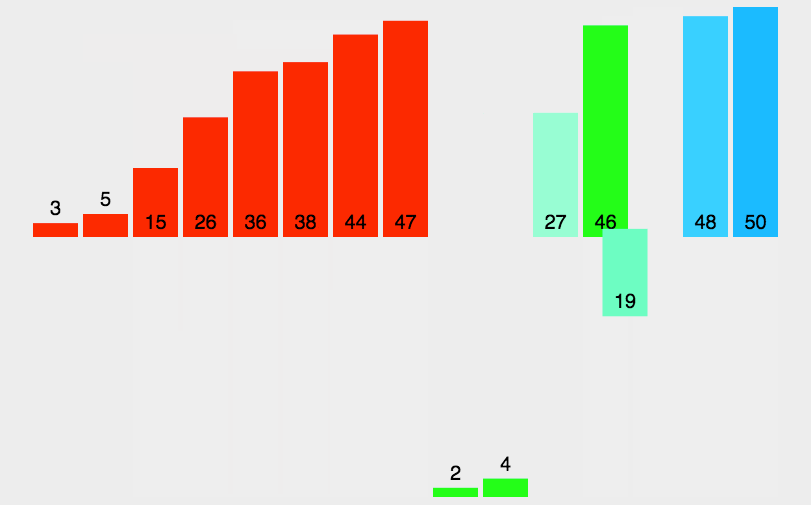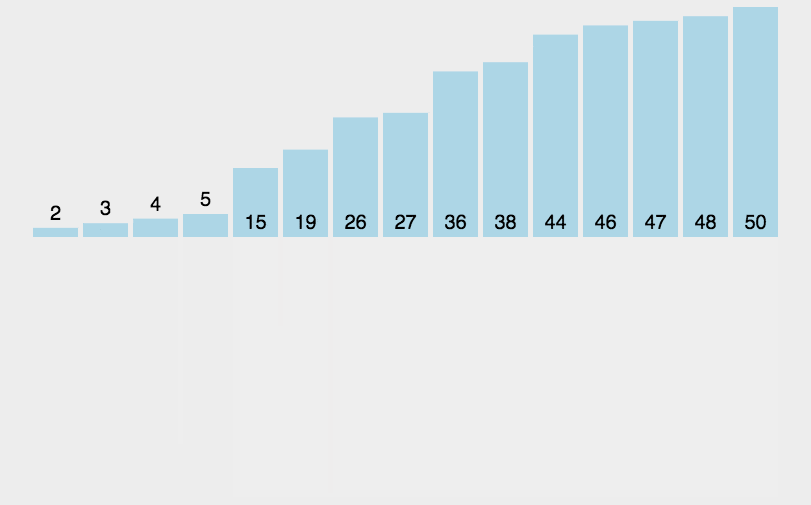
这个算法可以说是只要理解快速排序,直接拿捏了
直接看算法
def merge(L,R):
i, j = 0,0
# 用于存放L与R的合并内容
res = []
while i < len(L) and j < len(R):
if L[i] <= R[j]:
res.append(L[i])
i += 1
else:
res.append(R[j])
j += 1
res += R[j:] if i == len(L) else L[i:]
return res
def merge_sort(List):
length = len(List)
if length <= 1:
return List
else:
mid = length//2
left = merge_sort(List[:mid])
right = merge_sort(List[mid:])
return merge(left,right)
List = list(map(int,input().split(' ' )))
print(merge_sort(List))
首先进行一个读取数据
调用函数merge_sort
该函数与上述快排相差无几,只不过是从中值开始分的
返回值时调用函数
创建一个新列表,如果左侧大于右侧,将左侧数据通过append放置末尾
res += R[j:] if i == len(L) else L[i:]该语句负责将剩余的数据拼接到列表中
screen-20230117-134554