贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素。
一、选择排序
二、分割1221. 分割平衡字符串
三、买卖股票的最好时机(二)
四、55. 跳跃游戏
一、选择排序
选择排序是一种使用了贪心策略的算法,它确保每一次"遍历"都可以保证一个元素处于对应位置上.
每次选择一个最小或者最大的元素放在对应的位置上
void SelectSort(vector<int> num)
{
int n = num.size();
for (int i = 0; i < n; i++)
{
int Index = i;
// 用Index持续标记当前最小元素
for (int j = i; j < n; j++)
{
if (num[j] < num[Index])
Index = j;
}
swap(num[i], num[Index]);
}
Print(num);
}
void Print(vector<int> num)
{
for (auto e : num)
cout << e << " ";
cout << endl;
}二、分割1221. 分割平衡字符串
平衡字符串 中,'L' 和 'R' 字符的数量是相同的。
给你一个平衡字符串 s,请你将它分割成尽可能多的子字符串,并满足:
每个子字符串都是平衡字符串。
返回可以通过分割得到的平衡字符串的 最大数量 。
【解法一】动态规划思想根深蒂固之后,我就变得顾头顾尾了……
最终写下了下面这个代码,这个结果也异常醒目哈哈哈哈,忍不住炫耀一手
, 主要还是没有注意到题目给出的是一个已经平衡了的字符串,我还对j~i之间的区域进行判断
class Solution {
public:
bool Isbalance(string s)
{
int countL = 0;
int countR = 0;
int n = s.size();
for (int i = 0; i < n; i++)
{
if (s[i] == 'L')
countL++;
else
countR++;
}
return countL == countR;
}
int balancedStringSplit(string s) {
int n = s.size();
vector<int> dp(n+1, 1);
for(int i = 1; i < n; i+=2)
{
for(int j = 1; j < i; j+=2)
{
int len = i-j;
string temp = s.substr(j+1, len);
if(dp[j] && Isbalance(temp))
dp[i] = max(dp[i], dp[j]+1);
}
}
return dp[n-1];
}
};【解法二】使用俩个计数器即可,一个用来返回结果,一个用来验证是否平衡,如果遇到L那么balance++,如果遇到R那么balance--;如果balance为0,那么说明L==R所以进行一次分割,不需要管后面元素的情况(后面肯定是平衡的)

class Solution {
public:
int balancedStringSplit(string s) {
int cnt = 0;
int balance = 0;
for(int i = 0; i < s.size(); i++)
{
if(s[i] == 'L')
balance++;
else
balance--;
if(!balance)cnt++;
}
return cnt;
}
};【解法三】使用三目运算符优化一手

class Solution {
public:
int balancedStringSplit(string s) {
int res = 0;
int bal = 0;
for(int i = 0; i < s.size(); i++)
{
s[i]=='L' ? bal++ : bal--;
if(!bal)res++;
}
return res;
}
};三、买卖股票的最好时机(二)
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
【解法一】使用动态规划,之前的博客中以及详细处理了买卖股票的(一、二、三版本)这里直接手撕代码
俩个状态分别为第i天持股股最大值与第i天不持股的最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int> (2));
dp[0][0] = -prices[0];
dp[0][1] = 0;
for(int i = 1; i < n; i++)
{
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]);
}
return dp[n-1][1];
}
};【解法二】贪心策略
这种题解类似于一种马后炮的感觉,在现实生活中可能有这种情况嘛?好比我今天才知道了昨天阿根廷输了那么又无法改变自己昨天已经花了几十大洋买了阿根廷一样。
上面都是题外话,这里的贪心策略,更加注重的是每一天的盈利,假使只要第二天能赚钱我就卖掉,然后买新的,算当天的盈利,如果第二天下跌那就不算我的盈利。(真是够贪心的)
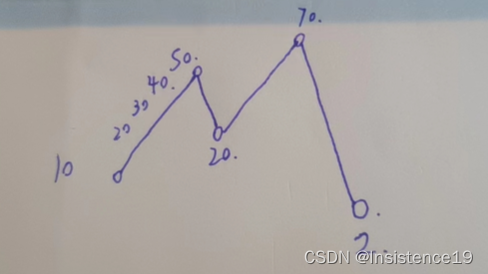
class Solution {
public:
int maxProfit(vector<int>& prices) {
int profit = 0;
for(int i = 1; i < prices.size(); i++)
// 如果第二天上涨,那么就在第一天买
if(prices[i] > prices[i-1])
profit += prices[i] - prices[i-1];
return profit;
}
};四、55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
也是一个贪心策略思想哈,每走一步都看自己当前这一步所能达到题目要求的最大长度。
class Solution {
public:
bool canJump(vector<int>& nums) {
int max = nums[0];
int n = nums.size();
if(n==1)return true; // 只有一个元素直接返回true
for(int i = 1; i <= max; i++)
{
int pos = i+nums[i]; // 记录当前结点所能到达的最远位置
max = pos>max?pos:max; // 更新max
if(max >= n-1) // 如果max可以到达最远位置返回true
return true;
}
return false;
}
};