方阵类型
https://leetcode.cn/problems/spiral-matrix-ii/
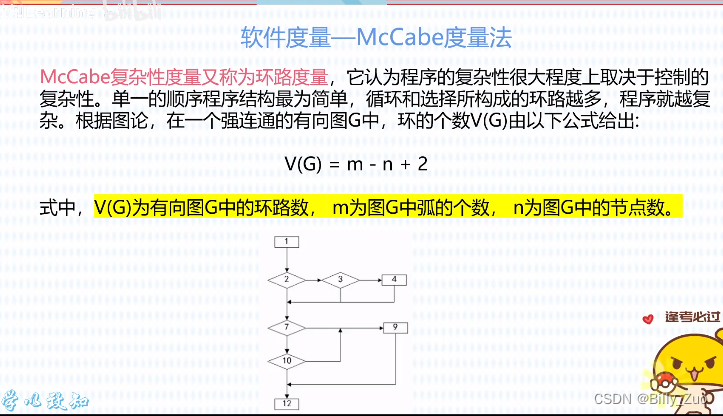
lc59: 螺旋矩阵, 解题思路
关键点:
- 上方, 从左到右; 右侧,从上到下; 下方,从右到左; 左侧, 从下往上, 逆序时, 使用range( start, end, -1) 的功能;
- 拐角处的数值,不在当前方向上进行赋值, 留给下一个方向上 作为初始值;
- range( start, end) 此时range 函数中的 初始值,需要指定,因为每次向内循环时, 起始位置和终止位置都在变换;
- 在四个方向都进行遍历一次后,开始向内循环, 此时需要对四个方向的, 起始位置+1, 终止位置-1;
- 当是奇数值矩阵时, 使用 下取整的方式, 将数值赋值给 矩阵的中心点数值;
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
left, right = 0, n-1
top, down = 0, n-1
result = [ [0]*n for _ in range(n) ]
val = 1
while left < right and top < down:
# 这里的关键点是,拐角处的边界值取不到, 拐角处的值留给下一个方向的初始值;
# 上方, 按照从左到右开始赋值; 此时,行号固定, x 递增;
for x in range(left, right):
result[top][x] = val
val = val +1
# 右侧, 按照从上到下开始赋值; 此时, 列号固定, y 递增;
for y in range(top, down):
result[y][right] = val
val = val +1
# 下方, 从右往左开始赋值;
for x in range(right, left, -1): # 使用数组倒着取值的性质; 注意, range 函数始终保持右边界值取不到;
result[down][x] = val
val = val +1
# 左侧, 从下往上开始赋值;
for y in range(down, top, -1):
result[y][left] = val
val = val + 1
# 遍历一层循环之后, 则开始往内层, 开始新的循环
# 此时, 起始位置 +1, 终止位置-1;
left = left +1
top = top +1
right = right -1
down = down -1
# 如果是奇数值矩阵, 则将当前的数值赋值给中心点;
if n%2 :
result[n//2][n//2] = val
return result
2. 非方阵类型
此代码的关键的核心思想,
- 每个方向上拐角处的边界值可以取到,
- 并且紧接着,下一个方向的起始位置往前移动一位, 其思想是因为上一个方向的拐角处的数值以及被上一个方向所包含了, 具体加一还是减一根据方向来判断。
- 经管在 while 循环中已经判断语句, 但是在内部循环过程中,仍然要增加两个添加判断语句, 用于确保访问的元素没有越界;
class Solution:
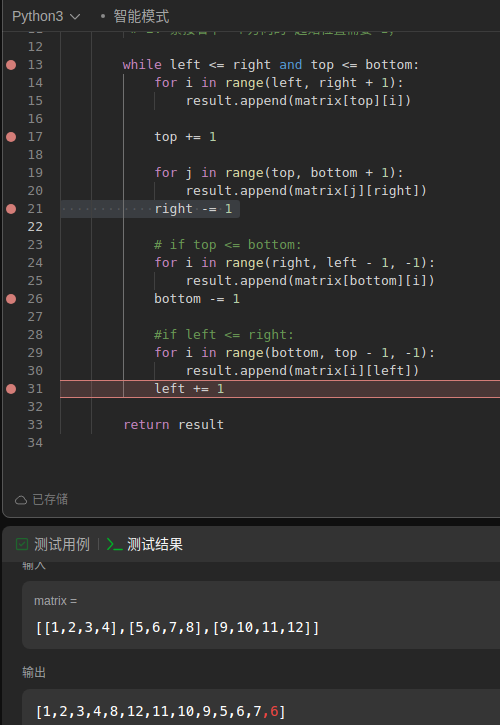
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
result = []
m, n = len(matrix), len(matrix[0])
left, right = 0, n-1
top, down = 0, m-1
while left<= right and top <= down:
# 上方从左到右,行号保持不变, 拐角处的位置数值取到, 并且将下一个方向的起始位置+1;
for x in range(left, right+1, 1):
result.append( matrix[top][x])
top = top +1
# 右边,从上到下, 列号保持不变, 拐角处的位置取到, 并将下一个方向的起始位置 +1;
for y in range(top, down+1, 1):
result.append( matrix[y][right] )
right = right -1
if top <= down: # 用于保证矩阵元素的访问没有越界;
# 下方从右往左, 行号保持不变, 拐角处的位置取到,
for x in range(right, left-1, -1):
result.append( matrix[down][x])
down = down - 1
if left <= right:
# 左侧,从下往上, 列号保持不变, 拐角处的位置取到, 并将下一个方向的起始位置+1;
for y in range(down, top-1, -1):
result.append(matrix[y][left])
left = left +1
return result
关于第三点的原因是,
在大循环中,已经有 top<= bottom and left<= right 的判断语句, 该判断作用 是用来判断 是否存在需要遍历的行 和列;
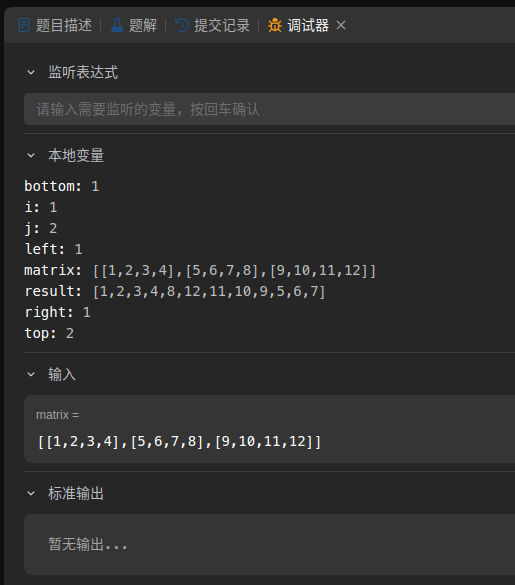
但是, 每次遍历后, top, down, left, right 的起始位置, 终止位置的数值都是在变化, 所以需要 使用 if top<= bottom 条件判断语句, 用来确保访问的元素没有越界, 即是在按照螺旋的方式在访问元素;
while top<= bottom and left <= right:
...
....
if top<= bottom:
for...
if left <= right:
for ....
如果我们删除这些条件,遍历可能会尝试访问矩阵当前边界之外的元素,从而导致:
-
越界错误:尝试访问矩阵索引有效范围之外的元素。
-
重复元素:重新访问已包含在结果中的元素。
-
不正确的顺序:由于边界超限,以不遵循螺旋模式的顺序添加元素。
该图中展示了 top > bottom 的情况, 属于边界超限, 从而导致重新访问元素;