3D 生成重建013-ProlificDreamer将SDS拓展到VSD算法进行高质量的3D生成
文章目录
- 0论文工作
- 1论文方法
- 2效果
0论文工作
**分数蒸馏采样(SDS)**通过提取预先训练好的大规模文本到图像扩散模型,在文本到3d生成方面显示出了巨大的前景,但存在过饱和、过平滑的问题g和低多样性问题。在这项工作中,作者提出将三维参数建模为一个随机变量,而不是像SDS中那样的一个常数,并提出了变分分数蒸馏(VSD),一个有原则的pa基于粒子的变分框架来解释和解决上述文本到3d生成中的问题。作者表明,SDS是VSD的一种特殊情况,会导致采样结果较差且CFG系数很大,这和过饱和关联密切。相比之下,VSD对不同的CFG权重作为扩散模型的祖先采样效果很好,同时使用共同的CFG权重提高了多样性和样本质量。
论文经典的套路,证明某个解法是我们算法的一个特例,我们提出的算法是更一般的更泛化的方案。不过这个论文的效果和对理论的扩展确实很独到的视角和很深刻的理论拓展。几乎是这两年看到对sds解释最全面的三篇文章了,Dreamfusion和SJC。更加详细的解释可以在作者论文中找到更详细的公式介绍。这是一个提升优化方法生成质量的一个答案,当然还有很多不同的角度去理解并缓解其中存在的问题。当我们从不同视角去看一个问题,得到的结论不同,也会有不统计解决思路。
ProlificDreamer
参考知乎
1论文方法
我们首先从2d图像生成理解这个问题,文本生成图像的时候,要在多样性和生成质量之间有一个权衡,这个开关用CFG系数来控制。CFG在2d的时候一般是10以内。这个系数越小我们对文本的依赖小生成结果会越多。越大的话就是生成结果越确定。通常要有一个权衡。
现在回到3d问题,那么每个视图怎么和原来文本保持尽可能的一致,就需要一个很大的CFG系数。这也是dreamfusion 过饱和比较严重的一个原因。cfg确实能支持整体风格的一致,但是在差不多1000次的优化步骤中,还是无法保证每次的生成结果朝着完全一致的方法,这就导致最终结果是在很多个优化方向中找一个中间状态,即缺乏细节,因为细节在平均过程中被相互抵消了。
接下来看一看ProlificDreamer作者的分析
∇
θ
L
SDS
(
ϕ
,
x
)
=
g
(
θ
)
≜
E
t
,
ϵ
[
w
(
t
)
(
ϵ
^
ϕ
(
Z
t
;
y
,
t
)
−
ϵ
)
∂
x
∂
θ
]
\nabla_{\theta} \mathcal{L}_{\text{SDS}}(\phi, x) = g(\theta) \triangleq \mathbb{E}_{t,\epsilon} \left[ w(t) \left( \hat{\epsilon}_\phi(Z_t; y, t) - \epsilon \right) \frac{\partial x}{\partial \theta} \right]
∇θLSDS(ϕ,x)=g(θ)≜Et,ϵ[w(t)(ϵ^ϕ(Zt;y,t)−ϵ)∂θ∂x]
对于一个用
θ
\theta
θ进行参数化的3D表示,给定文本 y ,通过对随机采样的视角下渲染的2D图像,优化SDS loss,就能让3D越来越逼真。
SDS 的更新方向有两个来源。首先,预训练的图像扩散模型引导渲染出的二维图像趋向真实。具体来说,扩散模型预测噪声大小,经线性变换后得到分布的 score,即似然函数的梯度(这部分与 SJC 从得分函数角度解释 DreamFusion 中 SDS 的方式一致)。此过程旨在最大化渲染图像的likelihood。而这种持续增大似然函数的行为,也称为“mode seeking”,本质上是在寻找似然函数的峰值。
SDS 的目标是在概率密度函数中寻找具有高似然度的模式。然而,在生成模型中,高似然度并不总是等同于高质量的生成结果。以高维高斯分布为例。高维高斯分布的典型样本和似然度最高的样本存在显著差异。对于一个
d
d
d 维的高斯分布
N
(
0
,
I
d
)
N(0, I_d)
N(0,Id),大部分概率密度集中在距离原点半径为
d
\sqrt{d}
d 的球面上,其样本类似于“雪花噪声”。然而,高维高斯分布的似然函数在原点 (全零向量) 处达到最大值,对应的样本是一张纯色图像,这显然不符合我们对高斯噪声样本的预期。高维高斯分布的典型样本与似然最大的样本很不一样。我们希望采到灰色圆环上的typical sample。

如下图所示,SDS的优化过程会让样本都偏离“典型样本”。并且由于不同的起始点可能都会收敛到同一个mode,所以还会导致多样性比较差。SDS的优化过程会让样本都偏离“典型样本”,并且还会导致多样性比较差。

为了解决上面提到的SDS的问题,VDS对SDS进行了一些小改动。我们同时优化多个样本,我们把样本们视为一个变分分布。如下图所示,把SDS更新方向的第二项由零均值的高斯换成了变分分布的Score。

额外的变分分布的score可以让样本收敛到图中灰色圆环上的典型样本,同时增大样本多样性。

这个变分分布在优化过程中会不断地变化,需要不断地更新对于变分分布score的建模。在这里作者用了LoRA,可以快速的学习变分分布。同时因为LoRA有一些先验知识,所以我们能够用很少量的样本就学到一个不错的score。

这个是论文结构图,用lora来学习变分分布。

2效果

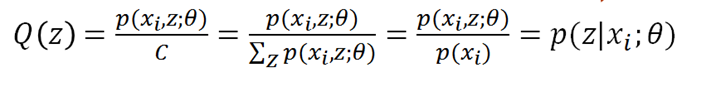





![[书生·浦语大模型实战营]——第二节:轻松玩转书生·浦语大模型趣味 Demo](https://img-blog.csdnimg.cn/direct/ff4423d65a6b4f6bb423bb6cb5f7f267.png)