机器学习是干什么的

我们目前处于大数据时代，每天会产生数以亿计的数据。如何让数据产生价值，机器学习应运而生！机器学习致力于研究如何通过计算手段，能够利用经验来改善系统自身的性能。 可以理解成：想办法让计算机自己分析某类问题的数据，总结一套规律，形成模型，以解决此类问题。如，把过去吃过的又香又甜的好西瓜什么颜色、根蒂弯不弯、敲声响不响，作为数据输入到计算机。计算机通过分析总结出什么样的瓜才是好瓜。之后我们去买瓜，挑瓜的时候把瓜的特征再输入到模型，模型就能告诉我们这个瓜好不好啦~

机器学习的理论基础: PAC模型

目的：能够稳定获得一个好的模型

解读

1. 解释括号内： 训练出好模型，即每次预测的平均误差能够小于一个值。比如1000次预测，出错的次数在200次以内，才算个好模型
2. 解释括号外的概率不等式： 稳定地得到好模型，由于划分数据集等各种因素的影响，模型的好坏也会随之浮动。我们想要不管其他因素怎么变化，我们都能在一定概率范围内得到好模型。

基本术语

关于数据

• 数据集：以上数据总称
• 示例、样本：每条数据
• 属性、特征：如，姓名、长相、工作、前任数量
• 属性值：如小黑是姓名属性的一个属性值
• 属性空间、样本空间、输入空间：以长相、工作、前任数量为三条坐标轴，小黑小白小王小李就是其中一个点，构成的空间
• 特征向量：每个点对应一个向量
  
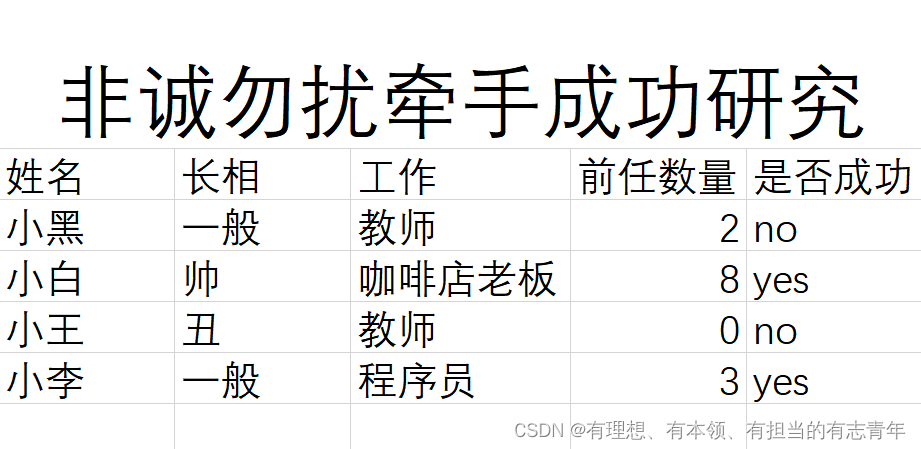
• 类别标记、标签：期望分类的结果，如是否成功
• 标记空间、输出空间：由类别标记形成的空间
• 样例：示例+类别标记

关于假设

计算机从中学到的数据潜在规律称为假设，如只要长相帅的就能牵手成功，就是一种假设。但是这种假设并不一定是正确的，男人帅还不够，工作也要稳定，帅可能只占了一定的比重，这也是一种假设。各种各样的假设便形成了假设空间。如：

西瓜色泽属性（青绿，乌黑，浅白，*），根蒂属性（蜷缩，稍蜷，硬挺，*），敲声属性（浊响，清脆，沉闷，*）以上特征组合考虑是好瓜的假设，再加上好瓜根本不存在的假设，即为假设空间，大小4*4*4+1=65

而版本空间是根据现有的数据集得出的所有假设，但是不代表所有可能的假设，版本空间是假设空间的子集

关于模型训练

计算机找到正确假设的过程称为学习、训练。在训练过程中，用到的数据叫做训练数据，每个样本称为一个训练样本。

学到模型后，我们想要检验它的好坏。检验的过程称为测试，被测试的样本称为测试样本。值得注意的是测试样本的结果是已知的，我们需要通过对比模型预测的结果和这个已知的结果的差别，来得出学到的模型的好坏。

我们千方百计训练出的模型，目的是为了预测新样本时会有不错的效果。模型对新样本预测能力的好坏，我们称为泛化能力。

这一切的前提都是在独立同分布的基础上，意思是说我们的现有数据集是相互独立的（你不能统计某一个家族的遗传病率来代表所有人的遗传病率），并且具有一定的代表性。（你不能在非洲统计白人的教育程度来预测世界上白人的教育程度）

机器学习任务分类

根据标签的类型主要分为分类任务和回归任务等。
分类任务：标签是一个个离散的值，如判断西瓜好坏，垃圾分类等
回归任务：标签是连续的值，如预测锅炉温度等

根据标签有无分为监督学习和无监督学习
监督学习：数据集有标签，能够预测与标签类型一致的结果
无监督学习：数据集没有标签，能够将自动将数据根据某一特征划分为一簇一簇，但是我们事先并不知道根据什么划分的

归纳偏好

奥克姆剃刀原则：选择最简单的模型
没有免费的午餐定理：没有一种模型能够适用于任何情况。

假如我们训练了两种模型，预测的准确率相差不大，但模型A却比模型B简单地多。根据奥克姆剃刀原则，我们会选择模型A。但是模型B一定差吗？未必。假如我们的评价标准发生改变，如在火灾预警上，我们宁愿没有发生火灾，但是发出了预警，也不愿意发生了火灾，但是并没有预警，因为这会让我们损失惨重。那么这时候模型B就可能会优于模型A。这便是没有免费的午餐定理。它让我们明白了脱离实际情况，谈论模型好坏毫无意义。

模型的评估和选择

我们把模型预测结果与真实结果之间的差异叫做误差
在训练集上得出的误差叫做训练误差
在未知样本上得出的误差叫做泛化误差

如果模型训练误差很大，那么证明模型还未完全拟合数据，叫作欠拟合
如果模型训练误差很小，但是泛化误差却很大，这是因为模型学习能力过于强，比如我们让模型学习什么样的东西是小狗，结果由于数据集中黄狗数量比较多，因此模型认为只有黄色的才是狗，成了名副其实的人工智障，这种现象叫做过拟合

训练流程

在一般情况下，我们对未知样本一无所知，无法获取到泛化误差。因此，我们用测试集上得出的测试误差来近似的表达泛化误差。那么到底什么是训练集？什么是测试集？又是怎么划分的呢？

在训练模型时，我们需要对数据集进行划分，首先按照一定比例划分训练集、验证集和测试集。测试集不能太大也不能太小，太大导致模型欠拟合，太小导致不具有代表性。其次我们把测试集扔在一边。通过训练集对模型训练，利用验证集调整参数，在保证不再改动的情况下，得出完善的模型。再将测试集输入模型，得出预测结果，与测试集实际结果计算误差，从而作为评价模型好坏的标准。最后，我们将整个数据集输入模型进行训练，得出最终模型，提交给客户。

划分数据集的方法

留出法

将数据集大约2/3~4/5的样本用于训练，其余用于测试。

• 注意分层采样，根据原来标签的比例进行划分，如原来的数据集中好瓜：坏瓜 = 6:4，那么划分数据集后，测试集中好瓜：坏瓜也应是6:4。
• 注意需要多次重复划分，最后取多次结果的平均值作为结果。

交叉验证

我们将数据集划分为K份，每次取其中1份作为测试集，其余K-1份作为训练集和验证集，总共进行K次训练和评估，最终把K次的结果取平均值，作为最终结果

• 缺点是测试集就取1份过少

自助法

前两种方法，都在一定程度上改变了训练样本的规模，都是取原数据集中的一部分进行训练。假设我们有m个样本，我们每次从中取出一个样本，加入到训练集，再将样本放回，进行m次，我们就得到了有m个样本的训练集。而仍会有数据集中约有1/3的样本未被取到，将它们作为测试集。

• 缺点：改变了原有数据分布

性能度量

均方误差：误差平方的平均值
精度：正确率
错误率：1-正确率

	预测为正类	预测为负类
实际为正类	TP	FN
实际为负类	FP	TN

查准率：TP/TP+FP
查全率：TP/TP+FN
F1值：2*查准率*查全率/（查准率+查全率）
宏查准率：多次结果的查准率的平均值
宏查全率：多次结果的查全率的平均值
宏F1：多次结果的F1值的平均值
P-R曲线：查准率关于查全率的变化曲线
ROC：真正例率关于假正例率的变化曲线
AUC：ROC曲线下的面积，越大证明模型越好
代价敏感错误率：适用于预测错误的代价有差别，如医疗诊断等