一.环形链表Ⅰ
. - 力扣(LeetCode)
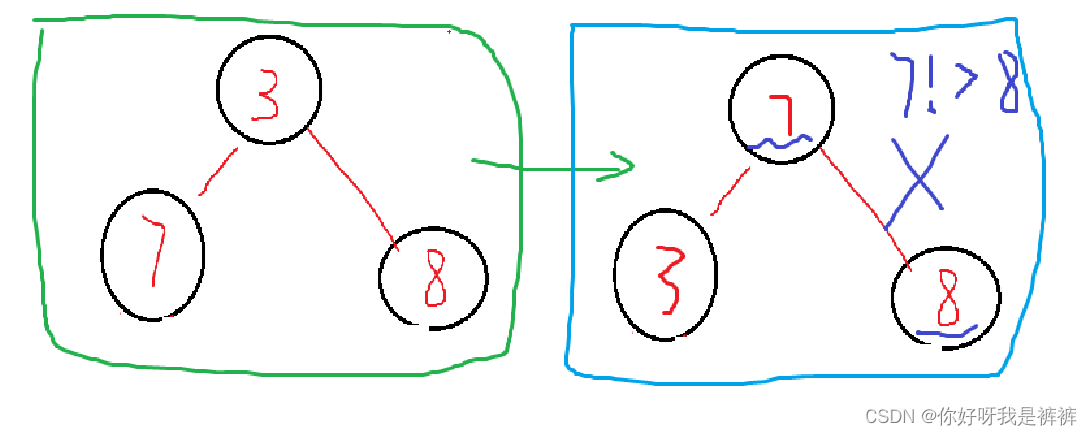
这道题可以利用快慢指针的方法来解决,即定义一个快指针f他的速度是一次走两步,慢指针s他的速度是一次走一步,这时我们假设链表有环,环的入口点为N,当两个指针一起向前走f会比s先进环内,当s走到环的如入口点N时,如下方第二个图,此时如果链表有环则两个指针都在环内,这时我们可以在做一个假设🧐,因为f的速度比s块,如果两个指针相遇了,那么这个链表就是有环的,如果f最后指向null了,那么说明,这个链表就是没有环的。
这样一看是不是感觉很简单🥰

接下来来实现我们的想法,首先定义两个节点f,s等于head,然后让f每次走两步,s走一步,期间判断f的下一个或下下一个是否为null(因为f一次走两步如果链表为偶数个,最后会只剩下一个节点),如果两个节点相遇则有环,否则无环。
代码如下(可以试着自己先敲一下)😊:
java

c

接下来我们看看一个进阶版的
二.环形链表Ⅱ
. - 力扣(LeetCode)
这道题是上一道的进阶版不过,原理相似都是利用快慢指针的方法解决😉,首先要判断链表有没有环,之后我们可以想一想如果如果两个节点相遇,那么肯定是f节点追上s节点(在入口相遇也算)😊,既然这样,f节点至少是要走一圈(因为想要和s相遇必然会再次经过入口点,假设一圈长度为C),再加上此时f离入口点的距离C-Y才行,又因为f的速度是s的二倍所以走的路程也是s的二倍🐱
 就可以得到一下表达式✌️:
就可以得到一下表达式✌️:
f=2s,f:X+C+(C-Y),s:X+(C-Y)
整理一下:
- X+C+(C-Y)=2(X+C-Y)
- X+2C-Y=2X+2C-2Y;
- 0=X-Y;
- X=Y;
是不是感觉很神奇😮,既然我们知道了X和Y一样那么,我们就可以让f节点再次等于head然后让两个节点以相同速度(一次走一步),向前走当两节点再次相遇时就是入口点🥰!!!是不是感觉更神奇了!✌️
不过你可能会有一个疑问🧐,如果环很小f在环内转了很多圈,这个等式是否还成立?🧐往下看:
f=2s,f=X+nC+(C-Y),s=X+C-Y
整理一下:
- X+nC+C-Y=2X+2C-2Y;
- (n-1)C = X-Y;
- X=Y+(n-1)C;
这时X好像不等于Y了呢🤔?继续往下看,我们依然让f=head让两个节点相前以相同速度走当,x走了(n-1)C步时,此时X离入口点的距离为Y,而s还在原地离入口点的距离也为Y,最后两节点依然会在入口点相遇😋!!
看吧都一样,以上就是这题的核心思路
代码如下(可以试着自己先敲一下)😊:
java

c

🐱以上是小编对这些题的理解如果有不懂的或者有哪里讲的不对的欢迎在下方评论😋,也请多多支持一下小编!!🥰🥰🥰