Pytorch入门（7）—— 梯度累加（Gradient Accumulation）

news2024/11/25 2:49:24

1. 梯度累加

在训练大模型时，batch_size 最大值往往受限于显存容量上限，当模型非常大时，这个上限可能小到不可接受。梯度累加（Gradient Accumulation）是一个解决该问题的 trick
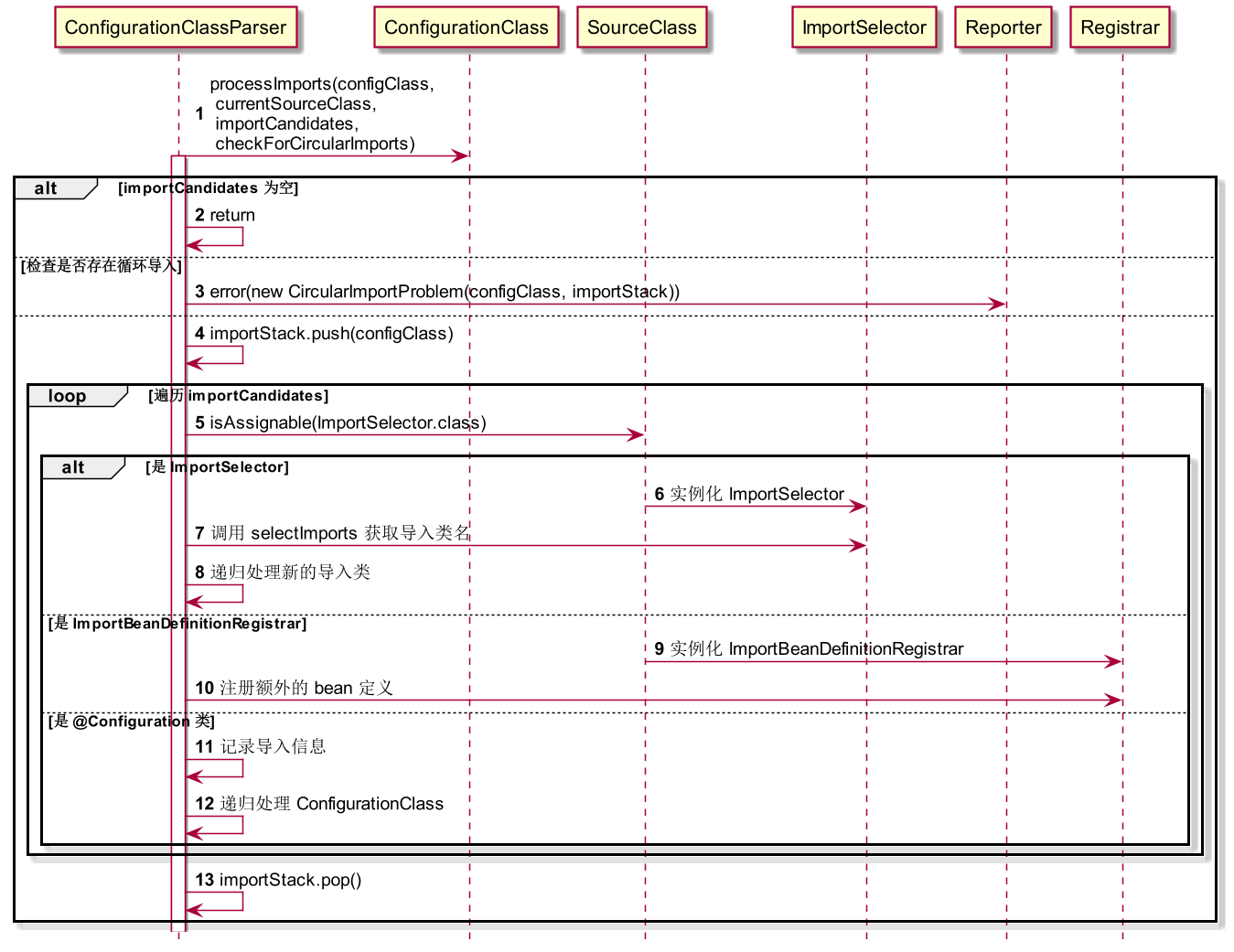
梯度累加的思想很简单，就是时间换空间。具体而言，我们不在每个 batch data 梯度计算后直接更新模型，而是多算几个 batch 后，使用这些 batch 的平均梯度更新模型，从而放大等效 batch_size。如下图所示
用公式表示：设 batch size 为 $n$ ，模型参数为 $\pmb{w}$ ，样本 $i$ 的损失为 $l_i$ ，则正常情况下 sgd 参数更新为
$\pmb{w} \leftarrow \pmb{w} + \alpha \sum_{i=1}^n\frac{1}{n}\frac{\partial l_i}{\partial \pmb{w}}$ 使用梯度累加时，设累加步长为 $m$ （即计算 $m$ 个 batch 梯度后用梯度均值更新一次），sgd 更新如下
$\begin{aligned} \pmb{w} &\leftarrow \pmb{w} + \alpha \frac{1}{m} \sum_{b=1}^m \sum_{i=1}^n\frac{1}{n}\frac{\partial l_{bi}}{\partial \pmb{w}} \\ &= \pmb{w} + \alpha \sum_{i=1}^{mn}\frac{1}{mn} \frac{\partial l_i}{\partial \pmb{w}} \end{aligned}$ 可见这等价于使用 batch_size = $mn$ 进行训练

2. 在 pytorch 中实现梯度累加

2.1 伪代码

pytorch 使用和 tensor 绑定的自动微分机制。每个 tensor 对象都有 .grad 属性存储其中每个元素的梯度值，通过 .requires_grad 属性控制其是否参与梯度计算。训练模型时，一般通过对标量 loss 执行 loss.backward() 自动进行反向传播，以得到计算图中所有 tensor 的梯度。详见 PyTorch入门（2）—— 自动求梯度

pytorch 中梯度 tensor.grad 不会自动清零，而会在每次反向传播过程中自动累加，所以一般在反向传播前把梯度清零

for inputs, labels in data_loader:
        
    # forward pass 
    preds = model(inputs)
    loss  = criterion(preds, labels)
	
	# clear grad of last batch	
	optimizer.zero_grad()
	
	# backward pass, calculate grad of batch data
	loss.backward()
	
    # update model
    optimizer.step()

这种设计对于实现梯度累加 trick 是很方便的，我们可以在 batch 计算过程中进行计数，仅在达到计数达到更新步长时进行一次参数更新并清零梯度，即

# batch accumulation parameter
accum_iter = 4  

# loop through enumaretad batches
for batch_idx, (inputs, labels) in enumerate(data_loader):
        
    # forward pass 
    preds = model(inputs)
    loss  = criterion(preds, labels)

    # scale the loss to the mean of the accumulated batch size
    loss = loss / accum_iter 

    # backward pass
    loss.backward()

    # weights update
    if ((batch_idx + 1) % accum_iter == 0) or (batch_idx + 1 == len(data_loader)):
        optimizer.step()
        optimizer.zero_grad()

2.2 线性回归案例

下面使用来自经典机器学习方法（1）—— 线性回归的简单线性回归任务说明梯度累加的具体实现方法

本节代码直接从 jupyter notebook 复制而来，可能无法直接运行！

首先生成随机数据构造 dataset

import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
import torch.utils.data as Data
import torch.nn as nn
import torch.optim as optim

# 生成样本
num_inputs = 2
num_examples = 1000
true_w = torch.Tensor([-2,3.4]).view(2,1)
true_b = 4.2
batch_size = 10

# 1000 个2特征样本，每个特征都服从 N(0,1)
features = torch.randn(num_examples, num_inputs, dtype=torch.float32) 

# 生成真实标记
labels = torch.mm(features,true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)

# 包装数据集，将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)

不使用梯度累加技巧，batch size 设置为 40

# 构造 DataLoader
batch_size = 40
data_iter = Data.DataLoader(dataset, batch_size, shuffle=False)	# shuffle=False 保证实验可比

# 定义模型
net = nn.Sequential(nn.Linear(num_inputs, 1))

# 初始化模型参数
nn.init.normal_(net[0].weight, mean=0, std=0)
nn.init.constant_(net[0].bias, val=0)

# 均方差损失函数
criterion = nn.MSELoss()

# SGD优化器
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 模型训练
num_epochs = 3
for epoch in range(1, num_epochs + 1):
    epoch_loss = []
    for X, y in data_iter:
        # 正向传播，计算损失
        output = net(X) 
        loss = criterion(output, y.view(-1, 1))
        
        # 梯度清零
        optimizer.zero_grad()            
        
        # 计算各参数梯度
        loss.backward()
        #print('backward: ', net[0].weight.grad)
        
        # 更新模型
        optimizer.step()
   
        epoch_loss.append(loss.item()/batch_size)
    print(f'epoch {epoch}, loss: {np.mean(epoch_loss)}')

'''
epoch 1, loss: 0.5434057731628418
epoch 2, loss: 0.1914414196014404
epoch 3, loss: 0.06752514398097992
'''

使用梯度累加，batch size 设置为 10，步长设为 4，等效 batch size 为 40

# 构造 DataLoader
batch_size = 10
accum_iter = 4
data_iter = Data.DataLoader(dataset, batch_size, shuffle=False)	# shuffle=False 保证实验可比

# 定义模型
net = nn.Sequential(nn.Linear(num_inputs, 1))

# 初始化模型参数
nn.init.normal_(net[0].weight, mean=0, std=0)
nn.init.constant_(net[0].bias, val=0)

# 均方差损失
criterion = nn.MSELoss()

# SGD优化器对象
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 模型训练
num_epochs = 3
for epoch in range(1, num_epochs + 1):
    epoch_loss = []
    for batch_idx, (X, y) in enumerate(data_iter):
        # 正向传播，计算损失
        output = net(X) 
        loss = criterion(output, y.view(-1, 1))  
        loss = loss / accum_iter	# 取各个累计batch的平均损失，从而在.backward()时得到平均梯度

        # 反向传播，梯度累计
        loss.backward()
        
        if ((batch_idx + 1) % accum_iter == 0) or (batch_idx + 1 == len(data_iter)):
            #print('backward: ', net[0].weight.grad)
            # 更新模型
            optimizer.step()              
            # 梯度清零
            optimizer.zero_grad()
        
        epoch_loss.append(loss.item()/batch_size)
    print(f'epoch {epoch}, loss: {np.mean(epoch_loss)}')
'''
epoch 1, loss: 0.5434057596921921
epoch 2, loss: 0.19144139245152472
epoch 3, loss: 0.06752512042224407
'''