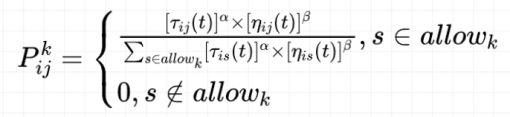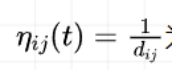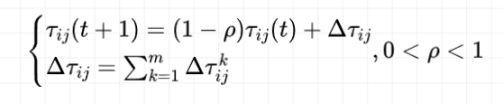人工智能应用-实验4-蚁群算法求解 TSP

news2024/11/26 10:05:38

文章目录

    • 🧡🧡实验内容🧡🧡
    • 🧡🧡代码🧡🧡
    • 🧡🧡分析结果🧡🧡
    • 🧡🧡实验总结🧡🧡

🧡🧡实验内容🧡🧡

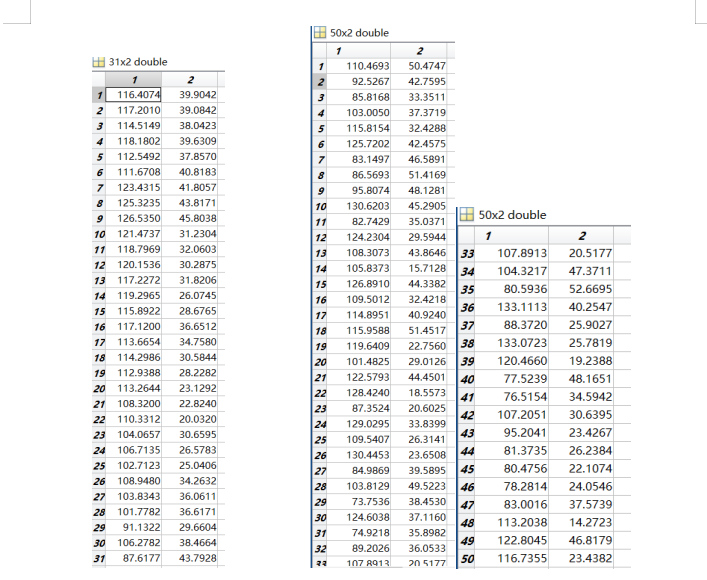
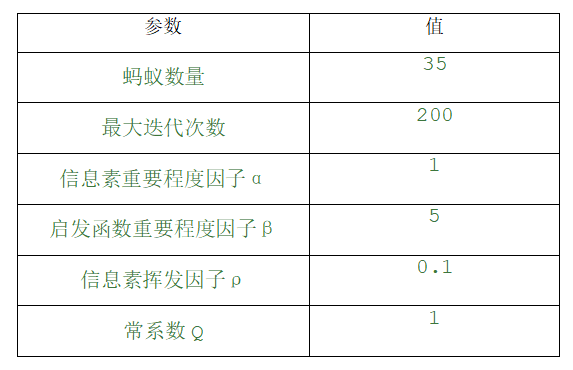
编写基于蚁群算法求解 TSP 问题的程序,分别求出 20 个城市之间和 50 个城市之间的最短路径。

🧡🧡代码🧡🧡

%% 清空环境变量
clear
clc
close all

%% 导入数据
citys_31 = [ % 内陆的31个主要省会城市，不含港澳台
    116.407395, 39.904211;
    117.200983, 39.084158;
    114.514862, 38.042307;
    118.180193, 39.630867;
    112.549248, 37.857014;
    111.670801, 40.818311;
    123.431475, 41.805698;
    125.323544, 43.817071;
    126.534967, 45.803775;
    121.473701, 31.230416;
    118.796877, 32.060255;
    120.153576, 30.287459;
    117.227239, 31.820587;
    119.296494, 26.074508;
    115.892151, 28.676493;
    117.120019, 36.651216;
    113.665412, 34.757975;
    114.298572, 30.584355;
    112.938814, 28.228209;
    113.264434, 23.129162;
    108.320004, 22.82402;
    110.33119, 20.031971;
    104.065735, 30.659462;
    106.713478, 26.578343;
    102.712251, 25.040609;
    108.948024, 34.263161;
    103.834303, 36.061089;
    101.778228, 36.617144;
    91.132212, 29.660361;
    106.278179, 38.46637;
    87.617733, 43.792818;
];
citys_50=[
    110.469286198181   50.4746691410186;
    92.5266910201309   42.7595185867962;
    85.8168137464198   33.3510745658952;
    103.005033088825   37.3718509138302;
    115.815409819431   32.4287938317344;
    125.720207837641   42.4575314260683;
    83.1496903823127   46.5890781381871;
    86.5692819178498   51.4168621571695;
    95.8073622632917   48.1280677266756;
    130.620267741678   45.2905464411555;
    82.7428601931531   35.0371447515392;
    124.230437470352   29.5943527737754;
    108.307261544677   43.8646083607653;
    105.837300942493   15.7127956890334;
    126.891027665425   44.3382449137088;
    109.501233625833   32.4217551748842;
    114.895073617088   40.9239984204817;
    115.95881   51.4517223372703;
    119.640883772243   22.7559646793684;
    101.482506618948   29.0125930804905;
    122.579272261262   44.4500855598353;
    128.423962506030   18.5572682527589;
    87.3523632932626   20.6025092238485;
    129.029503867517   33.8399355659161;
    109.540700690432   26.3141382912873;
    130.445329656714   23.6507514948169;
    84.9868745956852   39.5895240262594;
    103.812894324380   49.5222693078745;
    73.7535688054273   38.4530364608632;
    124.603837227041   37.1160006808058;
    74.9217946493522   35.8982407433328;
    89.2026003945863   36.0532693055382;
    107.891311021032   20.5177333856848;
    104.321662298107   47.3711070688777;
    80.5936363842351   52.6694785312550;
    133.111293665466   40.2547112805644;
    88.3720406809424   25.9026846100506;
    133.072259309913   25.7819126780322;
    120.466021232856   19.2388485754945;
    77.5238676167198   48.1650585535397;
    76.5154109411933   34.5941955801035;
    107.205075462786   30.6395114651284;
    95.2040830320626   23.4266972302777;
    81.3734952157783   26.2383951416844;
    80.4755943569925   22.1074033577527;
    78.2814334811311   24.0545780185756;
    83.0016130798109   37.5738520876487;
    113.203798272594   14.2722816613816;
    122.804520260080   46.8178856055774;
    116.735480758245   23.4382459106337;
];


%% 计算城市间相互距离
citys = citys_31;
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;
        end
    end    
end

%% 初始化参数
rng(66)                              % 随机因子，确保程序每次运行结果相同
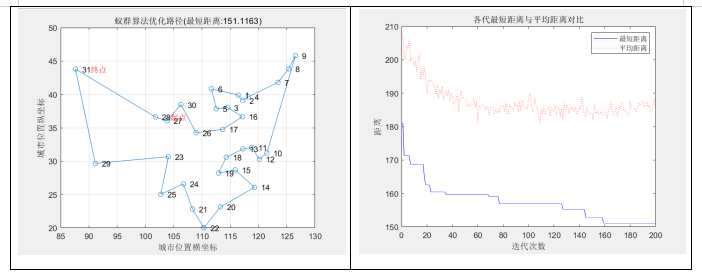
m = 35;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.1;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 200;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

tic; % 开始计时
%% 迭代寻找最佳路径
while iter <= iter_max
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));         % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha ...
                     * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
%               Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/D(j,j+1);
%               Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q;
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
%           Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/D(n,1); 
%           Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q; 
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表
    iter = iter + 1;
    Table = zeros(m,n);
end
elapsedTime = toc;% 结束计时

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
disp(['程序运行时间：', num2str(elapsedTime), '秒']);

%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点', 'Color', 'red');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点', 'Color', 'red');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

🧡🧡分析结果🧡🧡

为贴合现实情况，并且有利于研究TSP，我采用中国内陆的31个省会城市作为数据1，对于50个城市，我选择随机生成经纬度在一定范围内的城市坐标，然后保持起来，作为数据。
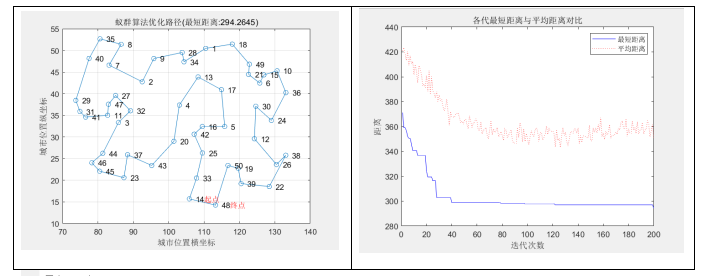
在这里插入图片描述
设置参数如下：
在这里插入图片描述
31个城市的最短路径图和迭代最佳距离变化图如下
在这里插入图片描述
在这里插入图片描述
改变为50个城市时：
得到50个城市的最短路径图和迭代最佳距离变化图如下
在这里插入图片描述
在这里插入图片描述

分析蚁群算法和遗传算法的区别与联系以及蚁群算法的优缺点
区别：
蚁群算法主要是模拟蚂蚁在寻找食物时释放信息素的过程，通过信息素的积累来更新路径，实现优化。
遗传算法主要是利用生物进化的思想，通过种群的选择、交叉、变异等基本操作，不断优化进化得到更好的解。
联系：
蚁群算法和遗传算法都是基于集体智慧的思想，通过群体中个体之间的交互和信息共享来实现全局最优化。
蚁群算法的优缺点：

  • 优点：
    蚁群算法能够较好地保持全局探索能力，避免陷入局部最优解。
  • 缺点：
    蚁群算法对于问题的参数敏感，需要进行较多的参数设置和实验，才能得到较好的效果。并且算法的收敛速度相对较慢，可能需要较长的时间才能达到最优解（这次实验普遍运行3秒以上，而实验二中用遗传算法求解TSP普遍1秒之内）。

🧡🧡实验总结🧡🧡

理论理解方面：
给我感觉是和粒子群类似，通过定义一些公式，来实现启发式搜索：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
简单来说就是对于所有蚂蚁，计算t时刻这只蚂蚁从城市i到城市j的概率，而这个概率与路径上信息素浓度相关，而信息浓度又与路径长度有关，因此让这只蚂蚁不断根据概率选择城市前往，在每一代从能得到这只蚂蚁的路径，也即一个解。对于信息素启发因子α，其值越大，表示信息素的浓度在转移中起的作用越大；β为启发函数重要程度因子，其值越大，表示启发函数在转移中的作用越大，即蚂蚁会以较大的概率转移到距离短的城市。当α=0时，算法就是传统的贪心算法，而当β=0时，就成了纯粹的正反馈的启发式算法。

代码实操方面：
有用到禁忌close表和open表，与BFS、DFS的搜索作用类似，记录哪些城市已经访问，哪些城市还没访问。实验中需要组合调试主要参数，而每次运行的收敛时间都相对来说比较长（也可能与我设置的迭代代数和城市规模过大有关），并且有时得出的解的质量其实并不能有太大差别，不敢保证搜到的就是全局最优，因此，对于城市规模较小的问题，可以先尝试使用其他算法求解理想最优值，以对实验结果进行更好的评估和判断。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1689004.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【GO基础】1. Go语言环境搭建

【GO基础】1. Go语言环境搭建

Go语言环境搭建 Go的三种安装方式Go标准包安装Windows 安装验证是否安装成功 4.Go的第一个程序 Hello World.go Go的三种安装方式 Go有多种安装方式&#xff0c;可以选择自己适合的。这里介绍三种最常见的安装方式&#xff1a; Go源码安装&#xff1a;这是一种标准的软件安装…
阅读更多...
【NumPy】NumPy实战入门：统计与聚合（histogram、percentile、corrcoef、cov）详解

【NumPy】NumPy实战入门：统计与聚合（histogram、percentile、corrcoef、cov）详解

&#x1f9d1; 博主简介&#xff1a;阿里巴巴嵌入式技术专家&#xff0c;深耕嵌入式人工智能领域&#xff0c;具备多年的嵌入式硬件产品研发管理经验。 &#x1f4d2; 博客介绍&#xff1a;分享嵌入式开发领域的相关知识、经验、思考和感悟&#xff0c;欢迎关注。提供嵌入式方向…
阅读更多...
如何解决vcruntime140.dll丢失问题，详细介绍5种靠谱的解决方法

如何解决vcruntime140.dll丢失问题，详细介绍5种靠谱的解决方法

vcruntime140.dll是Microsoft Visual C Redistributable Package的一部分&#xff0c;它为使用Visual C编译器开发的应用程序提供必要的运行时环境。该DLL文件包含了大量应用程序运行时需要调用的库函数&#xff0c;这些函数是实现C标准库、异常处理机制、RTTI&#xff08;运行…
阅读更多...
IO端口编址

IO端口编址

统一编址 特点 独立编址 特点 内存地址分配 区别 应用 IO端口地址译码 硬件上的实现 示例1&#xff1a; 示例2&#xff1a; IO指令 软件上的实现 示例
阅读更多...
golang通过go-aci适配神通数据库

golang通过go-aci适配神通数据库

1. go-aci简介 go-aci是神通数据库基于ACI(兼容Oracle的OCI)开发的go语言开发接口&#xff0c;因此运行时需要依赖ACI驱动和ACI库的头文件。支持各种数据类型的读写、支持参数绑定、支持游标范围等操作。 2. Linux部署步骤 2.1. Go安装&#xff1a; 版本&#xff1a;1.9以上…
阅读更多...
CleanMyMac X2024垃圾清理神器，让你的Mac保持飞速运行

CleanMyMac X2024垃圾清理神器，让你的Mac保持飞速运行

在数字时代的浪潮中&#xff0c;我们的苹果电脑扮演了至关重要的角色。然而&#xff0c;随着数据的增长和存储需求的不断上升&#xff0c;不合理的文件管理往往会导致系统性能逐渐下降&#xff0c;影响我们的工作效率。为了有效应对这一挑战&#xff0c;许多用户转向使用专为Ma…
阅读更多...
抖音运营_抖音电商介绍

抖音运营_抖音电商介绍

截止20年8月&#xff0c;抖音的日活跃数高达6亿。 20年6月&#xff0c;上线抖店 &#xff08;抖音官方电商&#xff09; 一 抖店的定位和特色 1 一站式经营 帮助商家进行 商品交易、店铺管理、客户服务 等全链路的生意经营 2 多渠道拓展 抖音、今日头条、西瓜、抖音火山版…
阅读更多...
MyBatisPlus使用流程

MyBatisPlus使用流程

引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.4</version> </dependency> 版本号根据需要选取 在实体类上加注解声明&#xff0c;表信息 根据数…
阅读更多...
7、按钮无法点击

7、按钮无法点击

不能点击&#xff0c;打开f12&#xff0c;删除disabled
阅读更多...
AIGC绘画设计基础-建筑设计应用

AIGC绘画设计基础-建筑设计应用

一、AI及AIGC 对于AI大家都不陌生&#xff0c;但是AIGC这个概念好多人其实不大清楚。“AI”是指人工智能技术本身&#xff0c;而“AIGC”是指基于人工智能技术而生成的内容。 生成式人工智能——AIGC&#xff08;Artificial Intelligence Generated Content&#xff09;&…
阅读更多...
Pod进阶——资源限制以及探针检查

Pod进阶——资源限制以及探针检查

目录 一、资源限制 1、资源限制定义&#xff1a; 2、资源限制request和limit资源约束 3、Pod和容器的资源请求和限制 4、官方文档示例 5、CPU资源单位 6、内存资源单位 7、资源限制实例 ①编写yaml资源配置清单 ②释放内存&#xff08;node节点&#xff0c;以node01为…
阅读更多...
阴影映射（线段树）

阴影映射（线段树）

实时阴影是电子游戏中最为重要的画面效果之一。在计算机图形学中&#xff0c;通常使用阴影映射方法来实现实时阴影。 游戏开发部正在开发一款 2D 游戏&#xff0c;同时希望能够在 2D 游戏中模仿 3D 游戏的光影效果&#xff0c;请帮帮游戏开发部&#xff01; 给定 x-y 平面上的…
阅读更多...
深度学习模型keras第二十一讲：使用BaseImageAugmentationLayer进行自定义图像增强

深度学习模型keras第二十一讲：使用BaseImageAugmentationLayer进行自定义图像增强

1、自定义图像增强技术概述 1.1自定义图像增强概念 深度学习的自定义图像增强技术是一种通过自定义的算法和策略对图像进行变换&#xff0c;以增加模型泛化能力和提高训练效果的技术。这些增强技术可以应用于各种深度学习任务&#xff0c;如图像分类、目标检测、图像分割等。…
阅读更多...
求第 N 个泰波那契数 | 动态规划

求第 N 个泰波那契数 | 动态规划

1.第 N 个泰波那契数 题目连接&#xff1a;1137. 第 N 个泰波那契数 泰波那契序列 Tn 定义如下&#xff1a; T0 0, T1 1, T2 1, 且在 n > 0 的条件下 Tn3 Tn Tn1 Tn2给你整数 n&#xff0c;请返回第 n 个泰波那契数 Tn 的值。 2.什么是动态规划 在解决这道问题之前…
阅读更多...
张大哥笔记：改变自己，才是改变一切的开始

张大哥笔记：改变自己，才是改变一切的开始

人往往有一种惰性&#xff0c;总喜欢把希望寄托于别人&#xff01;比如会将注意力投向外部因素如环境、他人或命运从而期望为我们的生活带来突破和转机。但现实往往是残酷的&#xff0c;不会发生任何改变的&#xff01;真正的改变来自于自己&#xff0c;自我革新才是改变整个局…
阅读更多...
cocos 通过 electron 打包成 exe 文件，实现通信问题

cocos 通过 electron 打包成 exe 文件，实现通信问题

cocos 通过 electron 打包成 exe 文件&#xff0c;实现通信问题 首先&#xff0c;我使用的 cocos 版本是 2.4.12&#xff0c;遇到一个问题&#xff0c;是啥子呢&#xff0c;就是我要把用 cocos 开发出来的项目打包成一个 exe 可执行程序&#xff0c;使用的是 electron &#xf…
阅读更多...
ArkUI-X开发指南：【SDK配置和构建说明】

ArkUI-X开发指南：【SDK配置和构建说明】

ArkUI-X SDK配置和构建说明 ArkUI-X SDK是ArkUI-X开源项目的编译产物&#xff0c;可将ArkUI-X SDK集成到现有Android和iOS应用工程中&#xff0c;使开发者基于一套ArkTS主代码&#xff0c;就可以构建支持多平台的精美、高性能应用。SDK内容包含ArkUI跨平台运行时&#xff0c;组…
阅读更多...
Java期末复习指南(1)：知识点总结+思维导图，考试速成！

Java期末复习指南(1)：知识点总结+思维导图，考试速成！

&#x1f516;面向对象 &#x1f4d6; Java作为面向对象的编程语言&#xff0c;我们首先必须要了解类和对象的概念&#xff0c;本章的所有内容和知识都是围绕类和对象展开的&#xff01; ▐ 思维导图1 ▐ 类和对象的概念 • 简单来说&#xff0c;类就是对具有相同特征的一类事…
阅读更多...
多线程、进程、线程五种状态、synchronized、volatile、Lock、CAS、死锁、ThreadLocal

多线程、进程、线程五种状态、synchronized、volatile、Lock、CAS、死锁、ThreadLocal

1、并发编程 并发编程三要素 原子性&#xff1a;只一个操作要么全部成功&#xff0c;要么全部失败可见性&#xff1a;一个线程对共享变量的修改&#xff0c;其他线程能够立刻看到有序性&#xff1a;程序执行的顺序按照代码的先后顺序执行 synchronized&#xff0c;Lock解决原…
阅读更多...
【HUST】信道编码｜基于LDPC码的物理层安全编码方案概述

【HUST】信道编码｜基于LDPC码的物理层安全编码方案概述

本文对方案的总结是靠 Kimi 阅读相关论文后生成的&#xff0c;我只看了标题和摘要感觉确实是这么回事&#xff0c;并没有阅读原文。 行文逻辑&#xff1a;是我自己设定的&#xff0c;但我并不是这个研究领域的&#xff0c;所以如果章节划分时有问题&#xff0c;期待指出&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023