[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第71讲。

跳房子游戏，本题是2021年10月24日举办的第13届蓝桥杯青少组Python编程选拔赛真题编程部分第5题。题目要求编程模拟跳房子游戏，计算出小明最少需要跳几次就可以完成游戏，完成游戏时哪只脚落地？

先来看看题目的要求吧。

一.题目说明

编程实现：

小明和同学们玩跳房子的游戏，现给出一排房子，请计算出小明最少需要跳几次就可以完成游戏，完成游戏时哪只脚落地？（0代表左脚，1代表右脚）

游戏规则1：

地上画有n个正方形依次排开代表房子，每个房子里标有数字，数字代表最多可以跳几个房子，数字不能为0（如：数字为2，可以直接向前跳1个房子，也可以直接向前跳2个房子）。

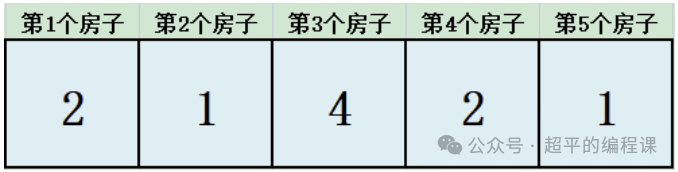
例如：

地上画有5个正方形代表房子，房子里面的数字分别为2，1，4，2，1。

小明在第1个房子时可以选择跳到第2个房子或者第3个房子，为了所跳次数最少选择跳到第3个房子（房子数字为4）；房间数字为4，可以选择跳到第4个房子或者第5个房子，为了所跳次数最少选择跳到第5个房子。故至少需要跳两次就可以完成游戏。

游戏规则2：

只能单脚落地，左脚起跳右脚落地，右脚起跳左脚落地；第一次起跳为左脚。

例如：

小明一共跳两次，第一次左脚起跳，右脚落地；第二次右脚起跳，左脚落地；完成游戏时左脚落地。

输入描述：

第一行输入n个正整数，正整数之间用英文逗号隔开

输出描述：

输出两个整数，整数之间用英文逗号隔开；第一个整数表示最少跳的次数，第二个整数表示落地的脚（0代表左脚，1代表右脚）

样例输入：

2，1，4，2，1

样例输出：

2，0

二.思路分析

这是一道算法题，涉及的知识点包括循环、列表、递归算法和动态规划等。

对于这个问题，首先能想到的是贪心算法，就是每次按照房间里的数字跳就行。

比如题目给出的样例，第一个房间数字为2，直接跳过两个房子，到第3个房间，然后跳过4个房间（实际上只需要跳过两个房间），就可以完成游戏，如图所示：

看起来好像是可以的，但是我们再换个测试数据看看， 如下：

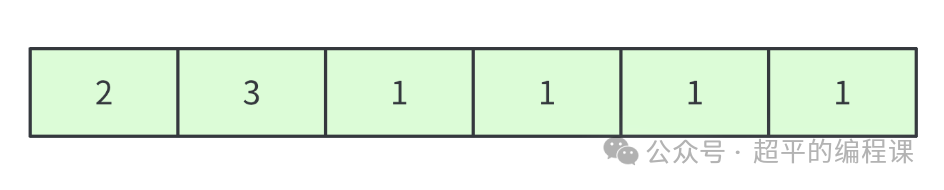
此时，如果采取贪心策略，第一次直接跳过两个房间，然后每次跳过一个房间，那么，一共需要跳4次才能完成游戏，如图：

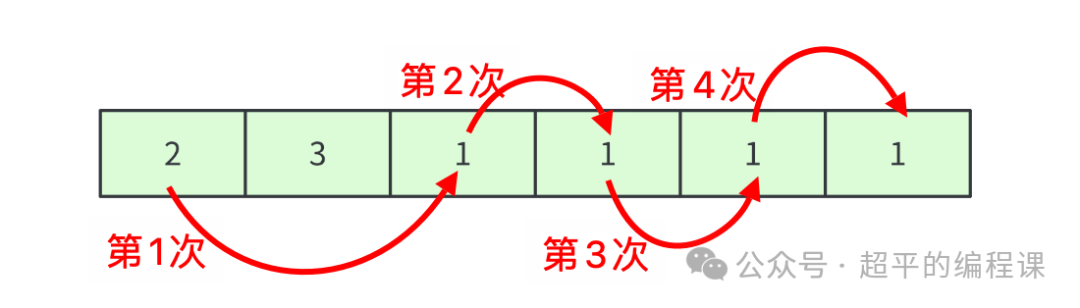
实际上，第一次只需要跳过一个房间，到达第二个房间，然后再跳过3个房间，这样一来，只要3次就可以完成游戏，如图：

这说明，贪心算法并不能解决这个问题，它只能获取每一步的最优解，但不一定是整个问题的最优解。

其实这个问题有点类似于爬楼梯，如图：

要爬到最顶层n，你可以从从第n - 1层上来，也可以从第n - 2层、n - 2层，甚至是第1层，只要你能一次跨越足够多的楼梯。

你站在每一层上，能够跨越的最大层数就是题目中所说的房间里的数字，如2，1，4，2，1。

所以，这是一个变种的斐波那契数列问题，假定f(n)表示到第n个房间的最小跳跃次数。那么，你可以从任意一个房间跳跃一次过了，有如下选择：

f(1)，如果可以跳跃f(2)，如果可以跳跃f(3)，如果可以跳跃...f(n - 1)，如果可以跳跃

所以，我们需要循环遍历前面所有的房间，从可以一次跳跃过来的房间中找到次数最少的那个房间。

如此一来，问题就比较明朗了，针对斐波那契数列问题，通常可以采用递归和动态规划等算法来实现。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们使用两种方法来编写程序：

• 递归算法

• 动态规划

1. 递归算法

根据前面的思路分析，我们先定义递归函数，如下：

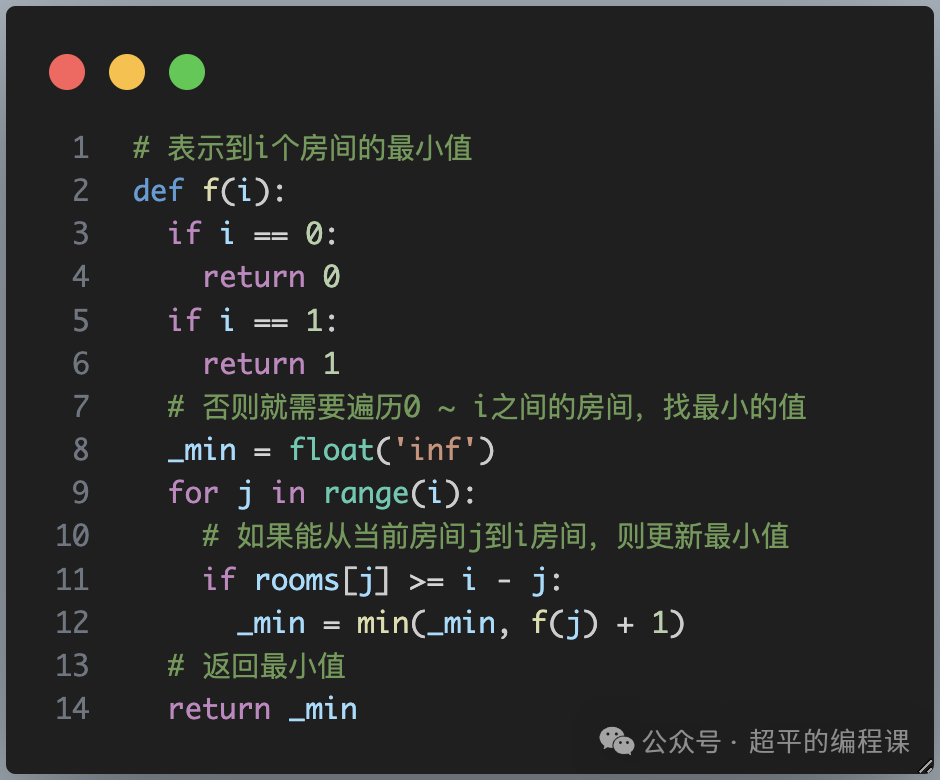
代码不多，说明3点：

1). 为了方便，这里用0表示第1个房间，1表示第2个房间，小明一开始就在第1个房间，不需要跳跃，所以返回0，要跳到第2个房间，一次就行，所以返回1；

2). 为了计算最小值，定义了遍历_min，同时将其设置为无穷大；

3). 对于任何一个房间i，都需要考虑从1 ~ i -1之间所有的房间，如果可以跨越，则计算其次数，然后获取最小次数。

接下来，获取输入的数据，调用函数处理即可，代码如下：

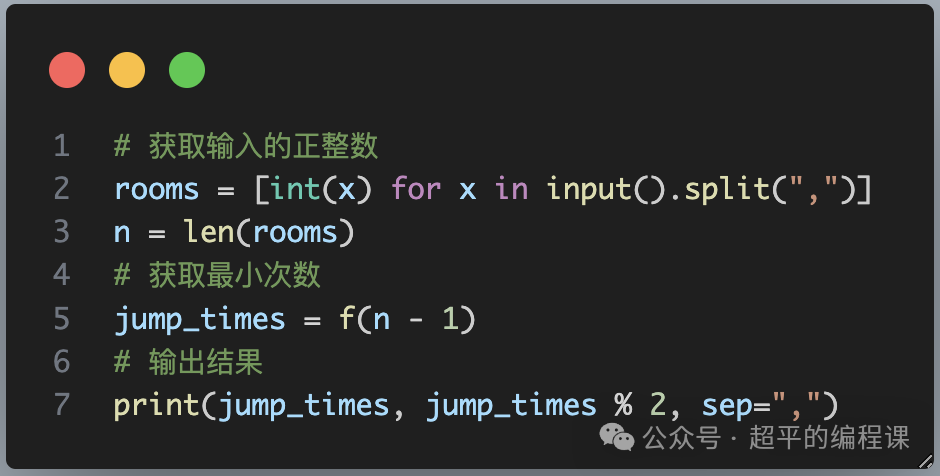
代码比较简单，说明两点：

1). 将输入的字符串，进行分解并转成整型，保存到rooms列表中，这里使用了列表推导式的编程技巧；

2). 计算最后落地脚是根据次数的奇偶性来判断的，如果是偶数，则为左脚，如果是奇数，则为右脚。

递归的代码比较好理解，但是有一个小问题，就是随着n的增加，时间复杂度和空间复杂度急剧增加，因为它包含了大量重复的计算。

通常情况下， 我们可以使用一个备忘录将已经计算过的房间保存起来，从而提升的代码效率，通常把这种递归称作带备忘录的递归。

修改代码如下：

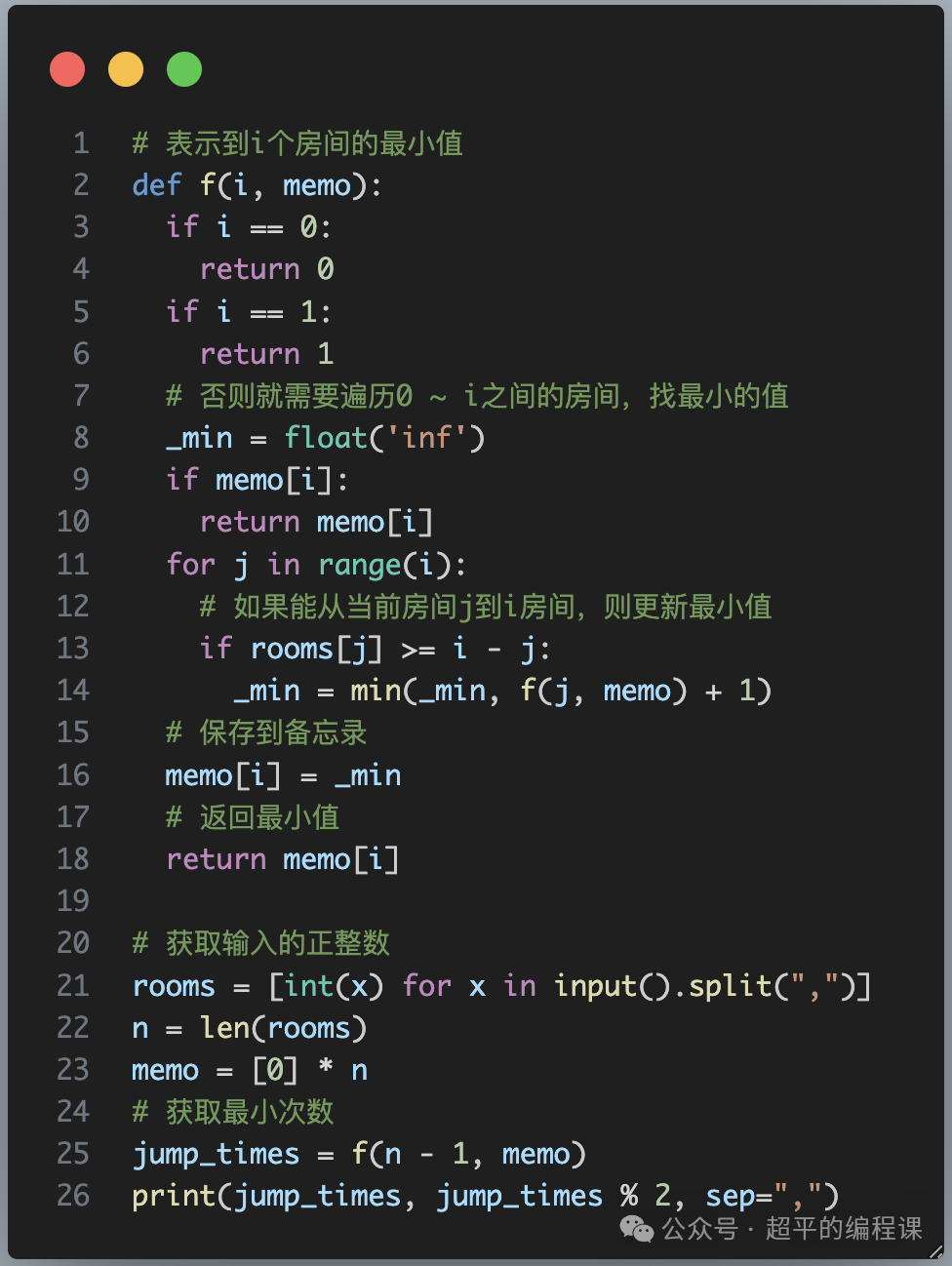
说明两点：

1). 函数增加了一个参数memo，它是一个列表，用来保存f(i)的值；

2). 在计算f(i)的值时，如果不为0，说明已经计算过，直接返回memo[i]，否则就计算f(i)的值，再保存到memo[i]中，然后返回。

2. 动态规划

使用动态规划的思想是先定义一个列表dp[i]，表示从第一个房间开始到达第i个房间的最小跳跃次数，确定好初始状态，然后使用循环挨个求解，从而得到最终的结果。

其代码如下：

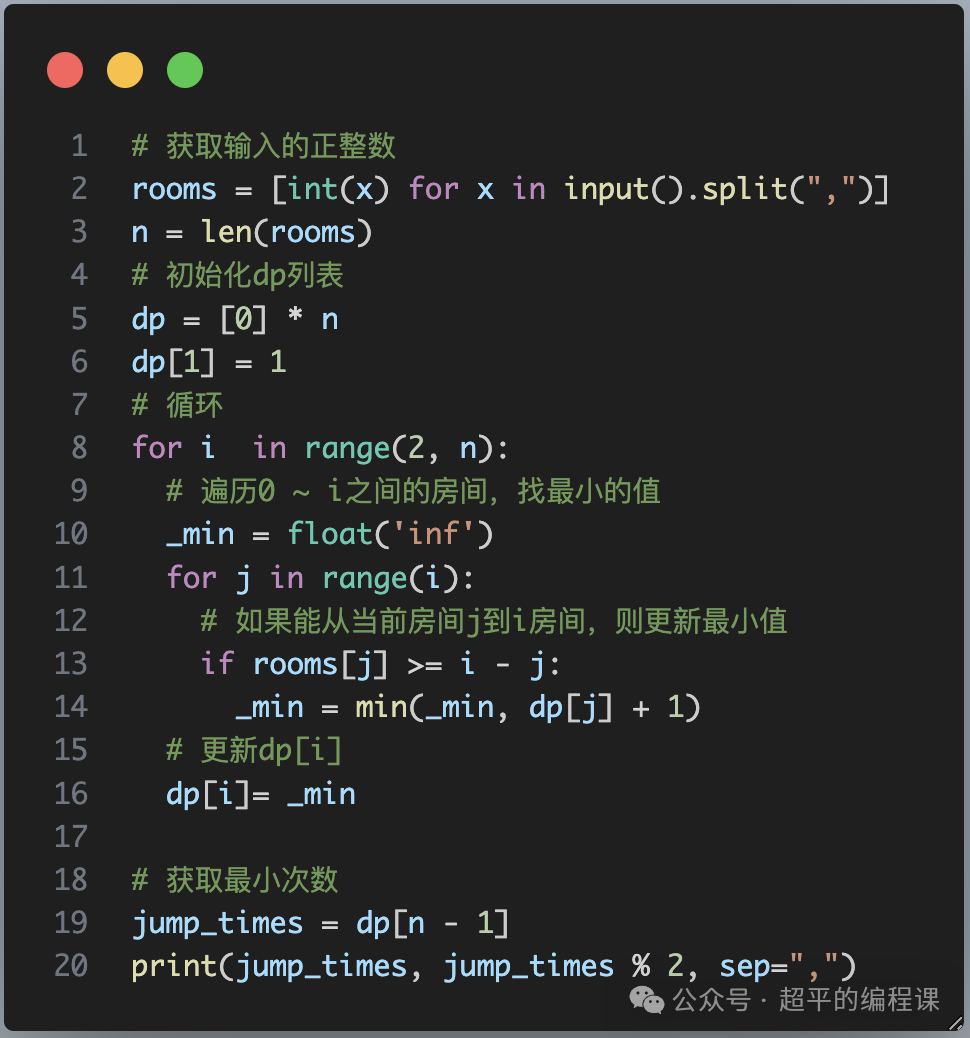
代码的意思和递归其实差不多，只是一个使用递归函数来计算f(i)，一个是使用循环来计算dp[i]。

至此，整个程序就全部完成了，你可以输入不同的数字来测试效果啦。

四.总结与思考

本题代码在15行左右，涉及到的知识点包括：

• 循环语句；

• 列表操作；

• 输入输出处理；

• 递归算法；

• 动态规划算法；

作为本次测评的最后一题，难度较大。关键点有两个，一是要彻底理解题目的意思，找到正确的解决方案，二是要善于将新问题转换为我们熟悉的问题，从而简化问题。

针对第一点，我们需要多列举几组不同特点的数据来进行分析测试，看看到底有什么规律，适合哪种算法。

对于求最值问题，常见的解决方案就是暴力枚举、贪心算法和动态规划，找到正确的方案至关重要了，一旦方向弄错了，后面的努力就都白费了。

针对第二点，这涉及到一个非常重要的学习理念--关联学习，什么样的学习最轻松、最有效，关联学习绝对是排得上号的。

一旦将本题和斐波那契数列关联起来，你会有一种豁然开朗的感觉，思路一下子完全打开了，这就是我们为什么要学习经典算法、经典案例的原因。

关于本题中使用的递归算法和动态规划算法，看起来完全不同，实际上关系非常密切。

它们有着相同的推导公式，有着相同的初始状态，所不同的是递归算法采取的是自顶向下，而动态规划采取的是自底向上。

实际上，凡是可以使用动态的地方，都可以使用递归算法来实现，而且强烈建议大家对于这类问题，一定要尝试使用两种算法来实现。

你还有什么好的想法和创意吗，也非常欢迎和超平老师分享探讨。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香😄

需要源码的，可以移步至“超平的编程课”gzh。