【机器学习】必会降维算法之：t-分布邻域嵌入（t-SNE）

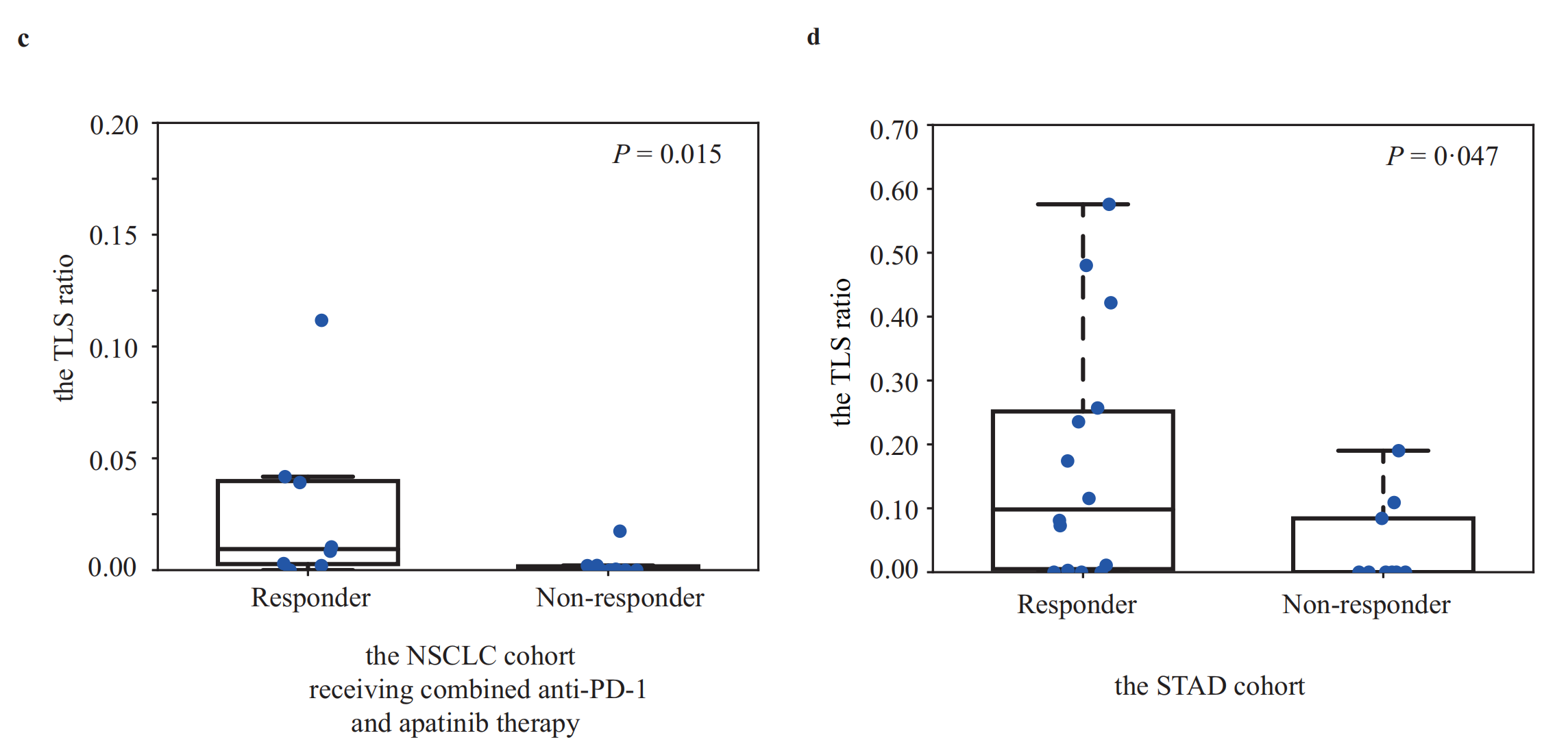
t-分布邻域嵌入（t-SNE）

1、引言
2、随机梯度下降（SGD）
- 2.1 简介
- - 2.1.1 定义
  - 2.1.2 应用场景
- 2.2 原理
- 2.3 实现方式
- 2.4 算法公式
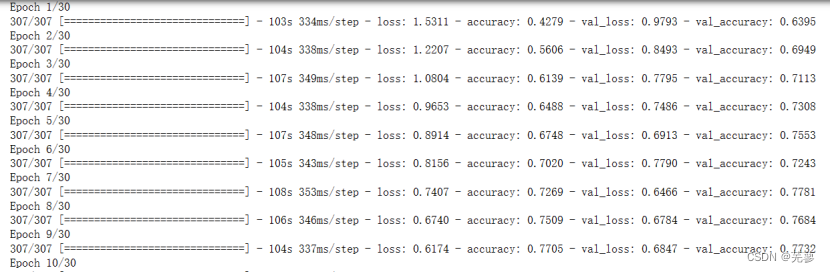
- 2.5 代码示例
- - 解析：
3、总结

1、引言

小屌丝：鱼哥，啥是降维算法
小鱼：我擦… 你是猴子派来搞笑的吗？
小屌丝：太浮躁了，当然要自鱼自乐
小鱼：说的不错，我正好买了钓竿，咱去试试
小屌丝：我看看你的钓竿
小鱼：给
在这里插入图片描述

小屌丝：哎呦喂，全套的，不错啊
小鱼：那你看，咱做事情，就是这么认真。
小屌丝：佩服，佩服，在下确实佩服。
小鱼：.走啊，钓场都联系好了
小屌丝：这么着急啊
小鱼：必须滴，必须得，
小屌丝：那去可以，前提是，跟我说一下t-SNE
小鱼：… 来吧，时间就是金钱，开整。

2、随机梯度下降（SGD）

2.1 简介

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种非常流行且有效的机器学习算法，用于高维数据的可视化。

它由Laurens van der Maaten和Geoffrey Hinton在2008年提出，目的是在低维空间（如二维或三维空间）中保持高维数据点的相对距离，从而便于我们通过可视化理解和解释数据的结构。

2.1.1 定义

t-SNE是一种统计方法，用于探索和可视化高维数据的结构。

它通过优化低维表示中的数据点位置，使得原始高维空间中相似的数据点在低维表示中保持接近，而不相似的点则远离。

2.1.2 应用场景

t-SNE的一些典型应用场景：

市场细分与消费者行为分析：营销专家可以通过t-SNE将消费者的购买历史、偏好和行为模式等高维数据降维到二维或三维空间，从而识别不同的消费者群体和市场细分，以及它们之间的潜在关系。
推荐系统：在推荐系统中，t-SNE可以帮助分析和理解用户的行为模式和偏好，进而提升推荐的准确性和个性化程度。通过对用户的历史行为和兴趣进行降维和可视化，可以更直观地了解用户的偏好和需求，从而提供更精准的推荐服务。
生物信息学：在生物信息学领域，t-SNE被用于降维基因表达数据，帮助研究者发现疾病与基因之间的关联，以及生物标记物的识别。通过t-SNE，可以将复杂的基因表达数据映射到低维空间，揭示其中的模式和结构，为疾病的诊断和治疗提供新的思路。
图像处理：t-SNE在图像分析中用于特征提取和降维，可以揭示图像数据中的模式和结构。例如，在图像分类、目标识别和异常检测等任务中，t-SNE可以帮助我们更好地理解和处理图像数据。
社交媒体分析：企业可以利用t-SNE分析社交媒体数据，识别社区结构、舆论动态和影响力人物。通过t-SNE的可视化结果，可以更直观地了解社交媒体上的用户行为和网络结构，从而制定更有效的社交媒体策略。

2.2 原理

t-SNE的核心思想是将高维空间中的欧式距离转换为条件概率来表示相似性。

对于低维空间，t-SNE使用了一种特殊的概率分布——t分布，以更好地处理不同密度区域的数据点，并减少不同簇之间的重叠。

相似度转换为概率：在高维空间中，数据点间的相似度通过高斯联合概率分布来表示；在低维空间中，相似度则通过t分布来表示。
KL散度最小化：t-SNE的目标是使得两个概率分布（高维和低维中的）之间的Kullback-Leibler (KL) 散度最小化。这通过梯度下降等优化算法实现。

在这里插入图片描述

2.3 实现方式

t-SNE的实现主要包括以下几个步骤：

计算高维空间中的相似度：使用高斯核函数计算每对数据点之间的相似度，得到条件概率分布P。
定义低维空间中的概率分布：在低维空间中，使用t分布（而非高斯分布）来计算数据点之间的相似度，得到条件概率分布Q。
最小化KL散度：使用KL散度来衡量P和Q之间的差异，并通过梯度下降等优化算法来最小化这个差异。
可视化：将优化后的低维表示进行可视化，展示数据的结构和关系。

2.4 算法公式

t-SNE中的关键公式主要包括：

高维空间中的条件概率分布P：对于高维空间中的数据点 $x i$ 和 $x j$ ，它们之间的条件概率 $p_{j|i}$ 由下式给出：
$p_{j|i} = \frac{\exp(-\lVert x_i - x_j \rVert^2 / 2\sigma_i^2)}{\sum_{k \neq i} \exp(-\lVert x_i - x_k \rVert^2 / 2\sigma_i^2)}$
其中， $\sigma_i$ 是以数据点 $x i$ 为中心的高斯方差。
低维空间中的条件概率分布Q：在低维空间中，使用t分布来计算数据点之间的相似度，得到条件概率分布Q。对于低维空间中的数据点 $y i$ 和 $y j$ ，它们之间的条件概率 $q_{j|i}$ 由下式给出：
$q_{j|i} = \frac{(1 + \lVert y_i - y_j \rVert^2)^{-1}}{\sum_{k \neq i} (1 + \lVert y_i - y_k \rVert^2)^{-1}}$
KL散度：用于衡量P和Q之间的差异，其公式为：
$\sum_i \sum_j p_{j|i} \log \frac{p_{j|i}}{q_{j|i}}$

2.5 代码示例

# -*- coding:utf-8 -*-
# @Time   : 2024-05-21
# @Author : Carl_DJ


from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import numpy as np

# X的高维数据集，这里用随机数据模拟
np.random.seed(0) # 设置随机种子以确保结果的可复现性
X = np.random.rand(100, 50) # 示例：100个样本，每个样本50维

# 初始化t-SNE模型
# n_components表示目标低维空间的维度（这里设置为2，以便可视化）
# perplexity是t-SNE的关键参数，可以视为近邻的数量，较小的数据集通常推荐使用较小的perplexity值
# n_iter是优化过程的最大迭代次数，增加此值可以提高模型稳定性
tsne = TSNE(n_components=2, perplexity=30, n_iter=1000, random_state=0)

# 对数据进行降维处理
X_tsne = tsne.fit_transform(X)

# 可视化降维后的数据
# X_tsne[:, 0]和X_tsne[:, 1]分别是降维后的两个维度
plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
plt.title('t-SNE visualization of high-dimensional data')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()

解析：

TSNE类是scikit-learn中实现t-SNE算法的主要工具。通过调整其参数，可以控制降维过程和结果的不同方面。
perplexity参数很重要，它影响着数据点之间的相对距离。选择合适的perplexity值对于获得有意义的可视化结果至关重要。通常，这个值应该根据你的数据集的大小进行调整。
n_iter参数指定了算法运行的迭代次数。对于大多数数据集，1000次迭代足以收敛到稳定的解，但是对于某些复杂的数据集，可能需要更多的迭代次数。
在可视化步骤中，我们简单地将降维后的数据点绘制在一个散点图上。每个点的位置都是基于其在降维后空间中的位置。

在这里插入图片描述

3、总结

t-分布邻域嵌入（t-SNE）是一种先进的非线性降维技术，尤其适用于高维数据的可视化。

通过将高维数据映射到低维空间（通常是二维或三维），t-SNE能够保留数据点的局部结构，使得在低维空间中，相似的数据点仍然保持相近的位置。

但是，在实施注意事项

参数调整：t-SNE的性能受到多个参数的影响，如困惑度（perplexity）、学习率（learning rate）等。在实际应用中，需要根据具体的数据集和任务进行参数调整。
数据预处理：在进行t-SNE降维之前，通常需要对数据进行适当的预处理，如标准化、去除噪声等。
可视化解释：虽然t-SNE能够提供直观的可视化结果，但解释这些结果时需要结合领域知识和实际背景进行。

我是小鱼：