1. 朴素贝叶斯算法

朴素贝叶斯(Naive Bayes)算法是一类基于贝叶斯定理的简单而强大的概率分类器,它在假设特征之间相互独立的前提下工作。尽管这种“朴素”的假设在现实中很少成立,但朴素贝叶斯分类器在许多实际应用中表现良好,特别是在文本分类和自然语言处理领域。下面是对朴素贝叶斯算法的详细介绍,包括其原理、优点、局限性和应用场景。
1.1 贝叶斯公式
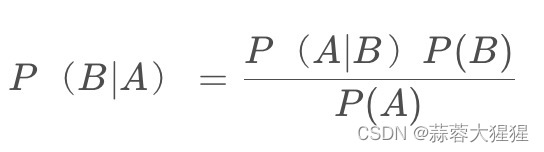
这是一个简单的贝叶斯公式,看不懂?让我们转换为中文:
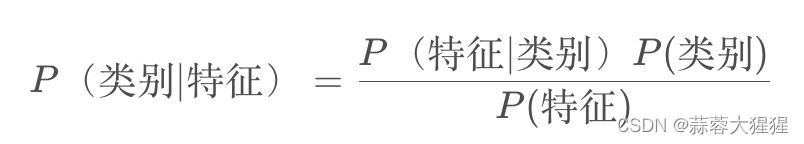
-P(类别|特征)是给定特征,类别的后验概率
-P(特征|类别) 是给定类别后,条件概率
-P(类别) 是类别的先验概率
-P(特征) 是特征的边缘概率
贝叶斯公式最基本的假设是条件之间相互独立,每个条件的变更不会影响其他条件的概率。
让我们来细讲一下:
P(类别)先验概率表示类别在样本集中出现频率,比如垃圾邮件占比60%,正常邮件占比40%
条件概率表示在某个类别下特征出现的频率,计算方法为在给定的类别样本中,某个特征出现频率,例如垃圾邮件共有20封,“免费”这个词在其中出现了2次,那么条件概率为2/20 = 1/10
那么组合一下,根据公式我们可以得到每个类别的后验概率,意义就是这些特征出现,那么特征为A&B的概率是多少。
朴素贝叶斯分类就是比较后验概率的大小,如果这个类别的概率比另一个大,那么我们认定其属于概率较大的类。
根据公式我们可以得知:


计算P(特征)可以抵消,实际上我们是在比较分子大小,那么计算分子大小就是算法的关键所在。
1.2 平滑处理
实际应用中,可能出现训练数据中某些特征在某个类别下从来没有出现,将会导致计算概率为0。为了解决这个问题,我们常使用拉普拉斯平滑:
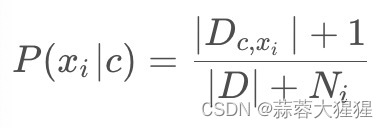
1.3 步骤分解
1. 计算先验概率 P(C) :
先验概率表示每个类别在训练数据中出现的频率。例如,如果我们有两类邮件,垃圾邮件和正常邮件,它们各自的比例是 30% 和 70%,那么P({垃圾邮件}) = 0.3 ,P({正常邮件}) = 0.7。
2. 计算条件概率P(x_i|C) :
条件概率表示在某个类别下特征出现的频率。例如,在垃圾邮件中,“免费”这个词出现的频率可能是 20%,而在正常邮件中可能是 1%。这些频率可以通过统计训练数据中的词频来计算。
3. 组合概率:
将先验概率和条件概率组合在一起,计算每个类别的后验概率。然后选择后验概率最大的类别作为预测结果。
1.4 举个例子
场景:垃圾邮件分类
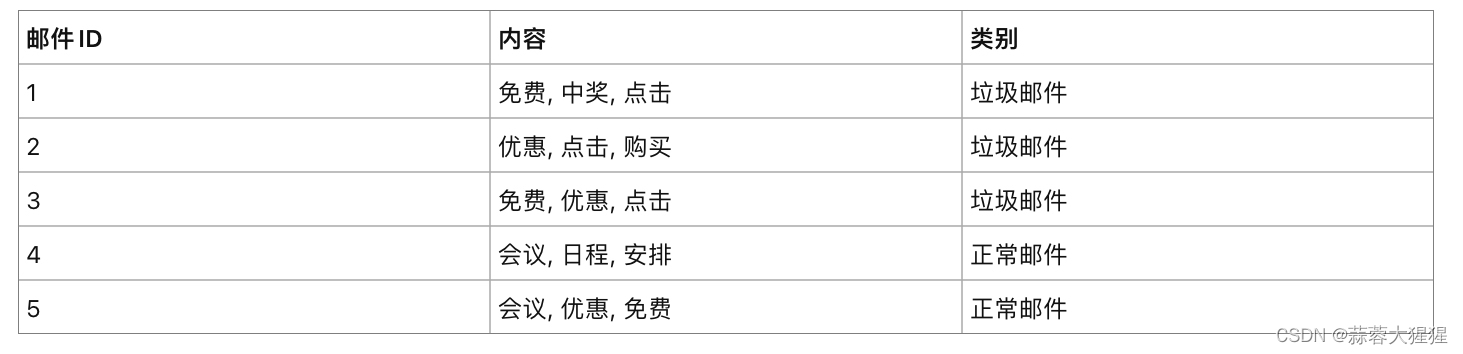
步骤1: 计算先验概率
P(垃圾邮件) = 3/5
P(正常邮件) = 2/5
步骤2: 计算条件概率:(这里用到拉普拉斯平滑)
垃圾邮件下的条件概率:
P(免费|垃圾邮件)= (2+1)/(9+5)= 3/14
P(中奖|垃圾邮件)= (1+1)/(9+5)= 2/14
P(点击|垃圾邮件)=(3+1)/(9+5)= 4/14
P(优惠|垃圾邮件)=(2+1)/(9+5)= 3/14
同理得到正常邮件的条件概率
步骤3:分类新邮件:
假设有一封新邮件,内容为“免费,点击,会议”,判断是属于什么类别的邮件

属于概率较大的一类
2. 手写代码实现
def loadData():
postList = [['my','dog','has','flea','problems','help','please'],
['maybe','not','take','him','to','dog','park','stupid'],
['my','dalmation','is','so','cute','I','love','him'],
['stop','posting','stupid','worthless','garbage'],
['mr','licks','ate','my','steak','how','to','stop','him'],
['quit','buying','worthless','dog','food','stupid']]
classVec = [0,1,0,1,0,1]
return postList,classVec
首先自定义一个数据集
def createVocabList(dataset): #包含在文档中不出现重复的词 相当于关键词集合
vocabSet = set([])
for document in dataset:
vocabSet = vocabSet | set(document) #求并集
return list(vocabSet)设置一个关键词字典
def setOfwords(vocabList,inputSet):
returnVec = [0]*len(vocabList) #创建与词汇表等长的零向量
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1 #word在关键词集合中的位置,在returnVec中同样的位置设定为1
return returnVec判断数据集中是否出现了我们所设置的关键词
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = np.ones(numWords)
p1Num = np.ones(numWords)
p0Denom = 2.0;p1Denom=2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = np.log(p1Num/p1Denom)
p0Vect = np.log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive
计算出先验概率以及条件概率
#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1) #前部分为频率*概率
p0 = sum(vec2Classify * p0Vec) + np.log(1-pClass1)
if p1 > p0:
return 1
else:
return 0最后判断比较每个类别的后验概率,得到分类结果。
3. 调包实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 初始化朴素贝叶斯分类器
nb_classifier = GaussianNB()
# 在训练集上训练分类器
nb_classifier.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = nb_classifier.predict(X_test)
# 计算分类器的准确率
accuracy = accuracy_score(y_test, y_pred)
print("朴素贝叶斯分类器的准确率为: {:.2f}".format(accuracy))4. 算法优点与局限性
4.1 优点
1. 简单易实现:朴素贝叶斯算法实现起来非常简单,计算复杂度低,适合大规模数据的处理。
2. 训练速度快:由于朴素贝叶斯只需要计算先验概率和条件概率,训练速度非常快。
3. 对小数据集有效:在数据量较小的情况下,朴素贝叶斯分类器仍能提供较好的性能。
4. 适用于多类分类:朴素贝叶斯天然支持多类分类问题,而无需进行复杂的调整。
5. 处理缺失数据:朴素贝叶斯能够在一定程度上处理缺失数据。
4.2 局限性
1. 特征独立性假设:朴素贝叶斯假设特征之间是相互独立的,这在现实中很少成立。特征之间的相关性可能会影响分类器的性能。
2. 概率估计不准确:朴素贝叶斯分类器的概率输出不一定准确,尤其在特征独立性假设不成立时。
3. 对零概率敏感:如果训练数据中某类特征组合从未出现过,条件概率会被估计为零,导致最终概率也为零。这通常通过平滑技术(如拉普拉斯平滑)来解决。
4. 数据量要求:尽管在小数据集上表现良好,但如果数据量过小,分类器可能会受到训练数据分布的极大影响。
5. 应用前景
1. 文本分类:
- 垃圾邮件过滤:通过分析电子邮件中的词频来判断邮件是否为垃圾邮件。
- 情感分析:根据文本中的词语分布来判断文本的情感倾向(如积极、消极)。
- 主题分类:将文档自动分类到不同的主题类别中。
2. 文档分类:
- 新闻分类:根据新闻文章的内容自动将其归类到不同的新闻类别。
- 电影评论分类:根据用户评论内容,判断其对电影的评价(如好评、中评、差评)。
3. 医疗诊断:
- 疾病预测:根据病人的症状和体征,预测其可能患有的疾病。
4. 推荐系统:
- 产品推荐:根据用户的历史行为和偏好,推荐可能感兴趣的产品。
5. 图像处理:
- 图像分类:根据图像的像素值或特征进行分类。
6. 参考资料
机器学习(五)——朴素贝叶斯-CSDN博客