(1)单源点最短路径问题
问题描述:
给定一个图,任取其中一个节点为固定的起点,求从起点到任意节点的最短路径距离。
例如: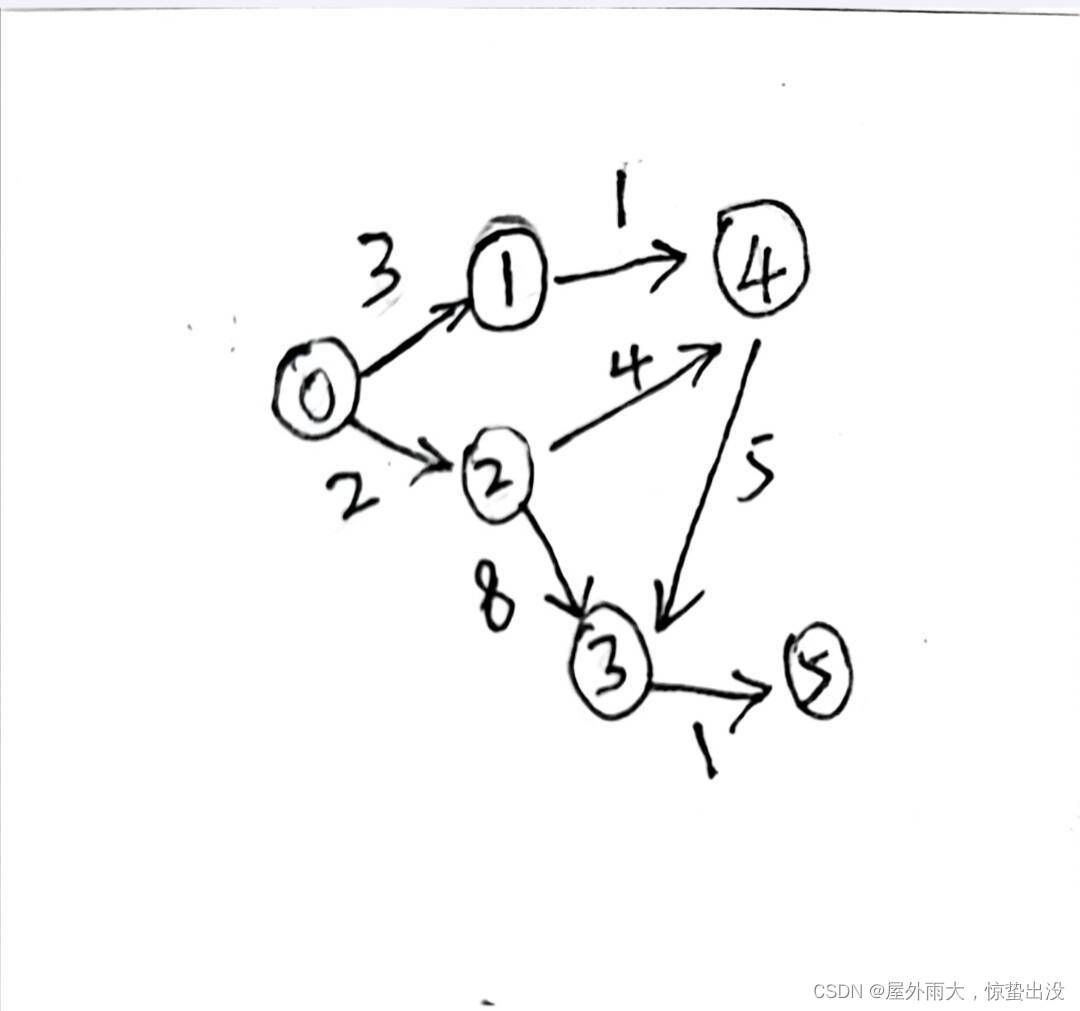
思路与关键点:
以下代码中涉及到宏INT_MAX,存在于<limits.h>中。

首先,建立三个数组dist,S,W,prev分别用来存储从起始节点到任意节点的最短距离;相对于s距离起点的最短路径节点集合;存储要遍历的图的各条边的距离;用来存储各个节点的直接前驱节点。
3个主要的个功能函数。
(1)minDistance函数用来寻找V-S集合中的距离起点的最短距离,并返回该节点的下标。
(2)dijkstra函数用来寻找从起始节点到任意节点的最短路径长度。
思路是把节点分为两类,一类是没有放进S集合中的节点,一类是已经放进去的节点。那么,寻找从起始节点到节点v的最短路径就有两种可能的取值。
第一种是组成该最短路径的就是dist[v]。
第二种是新加入S集合的节点u可能会组成一个新的更短的路径,这时,要更新dist[v]。
(3)Traceback函数用来打印从源点到终点的路径。这个函数基于prev数组,该数组建立的核心原理是:每次更新dist数组,一定是因为s集合中增加了一个节点u,这个u一定是当前更新dist[v]的直接前驱节点。递归调用,不断找前一个前驱节点,就可以打印出完整路径了。
伪代码:

代码:
#include <iostream>
#include <limits.h>
using namespace std;
#define V 6 // 节点的数量
void Traceback(int v, int i, int prev[]);
int minDistance(int dist[], int S[]);
void printSolution(int dist[]);
void dijkstra(int W[V][V], int src);
int main() {
int W[V][V] = {{0, 3, 2, 0, 0, 0},
{0, 0, 0, 0, 1, 0},
{0, 0, 0, 8, 4, 0},
{0, 0, 0, 0, 0, 1},
{0, 0, 0, 5, 0, 0},
{0, 0, 0, 0, 0, 0}};
dijkstra(W, 0);//起始节点为节点 0
return 0;
}
// 找到距离数组中最小值的索引
int minDistance(int dist[], int S[]) {
int min = INT_MAX, min_index;
for (int j = 0; j < V; j++) {
/*
如果节点j没有包含在最短路径数组中,初始时,只要有路径,就更新最短路径数组的值。
后面,每次进入循环都与当前的最短距离进行比较,更新。找到V(全部节点集合)-S(已找到的最短路径节点集合)中距离起点最短的路径的节点编号。
*/
if (S[j] == 0 && dist[j] <= min) {
min = dist[j];
min_index = j;
}
}
return min_index;
}
// 打印最终的最短路径
void printSolution(int dist[]) {
printf("节点\t最短距离\n");
for (int i = 0; i < V; i++)
printf("%d\t%d\n", i, dist[i]);
}
// Dijkstra算法的实现
void dijkstra(int W[V][V], int src) {
int dist[V]; // 存储从源节点到每个节点的最短距离
int S[V]; // 记录节点是否已经包含在已找到的最短路径节点集合中
int prev[V];
// 初始化所有距离为无穷大,标记所有节点为未包含
for (int i = 0; i < V; i++) {
dist[i] = INT_MAX;
S[i] = 0;
}
// 设置起始节点的距离为0
dist[src] = 0;
// 找到最短路径
for (int count = 0; count < V - 1; count++) {
// 选择距离最小的节点
int u = minDistance(dist, S);
// 标记节点为已包含
S[u] = 1;
// 更新相邻节点的距离
for (int v = 0; v < V; v++) {
/*如果该节点没有包含在最短路径数组中,有路径可直接到达该节点,并且有路径可达该节点,
并且,从节点0到节点u的最短路径长度,与,从节点u到节点v的路径距离之和小于从节点0到该节点当前最短距离,
则更新最短距离。
*/
if (!S[v] &&W[u][v] && dist[u] != INT_MAX &&
dist[u] +W[u][v] < dist[v]) {
dist[v] = dist[u] + W[u][v];
prev[v]=u;
}
}
}
// 打印最终的最短路径
printSolution(dist);
int v,i;
printf("请输入源点及终点");
cin>>v>>i;
printf("从源点%d到终点%d的最短路径为:\n",v,i);
Traceback(v,i,prev);
}
//输出最短路径 v源点,i终点,
void Traceback(int v, int i, int prev[])
{
// 源点等于终点时,即找出全部路径
if (v == i)
{
cout << i;
return;
}
Traceback(v, prev[i], prev);
cout << "->" << i;
}
运行结果:
关键步骤证明:
时间复杂度与空间复杂度:
时间复杂度为0(
),空间复杂度为0(
)。
(2)活动选择问题
问题描述:
假定有一个n个活动的集合S={a1,a2,……,an},这些活动使用同一个资源,而这个资源在某个时刻只能供一个活动使用。每个活动有一个开始时间si和一个结束时间fi,其中0<=si<fi<∞。如果被选中,任务ai发生在半开时间区间[si,fi)期间。如果两个活动ai和aj满足[si,fi)和[sj,fj)不重叠,则称他们是兼容的.也就是说,若si>=fj或sj>=fi,则ai和aj是兼容的。
在活动选择问题中,我们希望选出一个最大兼容活动集。
例子: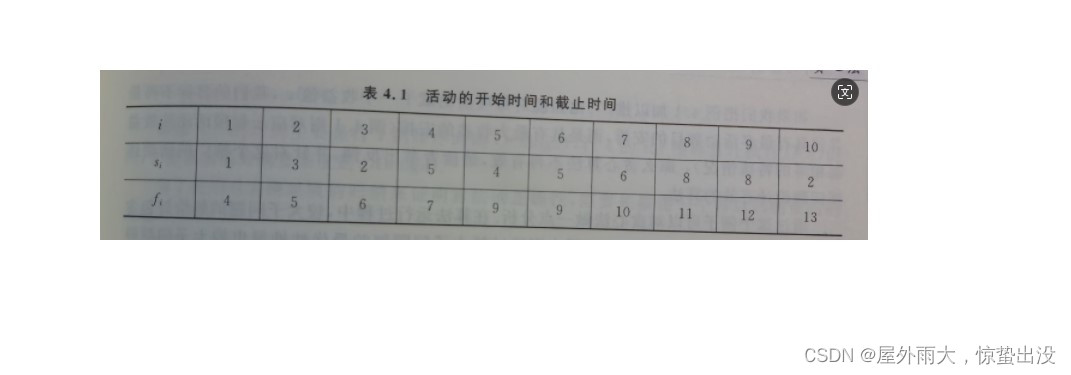
该活动序列的最大兼容活动集为1,4,8或1,4,9
思路与关键点:
按活动结束时间从小到大排序
每次选择的活动将作为是否与下一个活动兼容的判断依据。
伪代码:

代码:
#include<iostream>
#include<string.h>
using namespace std;
void Traceback(int Trace[],int n);
void sort(int n,int *s,int* f)
{
int a,b,i,j;
//冒泡排序,按结束时间从小到大排列活动
for(i=1;i<n;i++)
{
for(j=1;j<n-i+1;j++)
{
if(f[j]>f[j+1])
{
a=f[j];
f[j]=f[j+1];
f[j+1]=a;
b=s[j];s[j]=s[j+1];s[j+1]=b;
}
}
}
}
int GreedySelect(int n,int s[],int f[],bool A[])
{
int Trace[n];
Trace[1]=1;
A[1]=true;//第一个活动必然在最优解中
int j=1,count=1;
//从第二个活动开始,寻找下一个兼容的活动
for(int i=2;i<=n;i++){
if(s[i]>=f[j]){
A[i]=true;
j=i;//将已经选人的最后一个活动标号作为下一次比较兼容的参照
count++;
Trace[count]=i;
}
else A[i]=false;
}
Traceback(Trace,count);
return count;
}
//打印的活动序列是按照结束时间从小到大排好序的活动序列,而不是原来的活动序列
void Traceback(int Trace[],int n){
printf("活动安排顺序为:");
for(int i=1;i<=n;i++){
cout<<"->"<<Trace[i];
}
cout<<endl;
}
int main(){
int n,s[50],f[50];
bool A[50];
memset(A,false,sizeof(A));
printf("请输入活动个数:\n");
cin>>n;
//活动标号与数组下标保持一致,从1开始标号
for(int i=1;i<=n;i++){
printf("请输入第%d个活动的开始时间和结束时间\n",i);
cin>>s[i]>>f[i];
printf("第%d个活动的开始时间是%d,结束时间是%d\n",i,s[i],f[i]);
}
sort(n,s,f);
printf("最多相容活动数为:\n");
cout<<GreedySelect(n,s,f,A)<<endl;
return 0;
}运行结果:
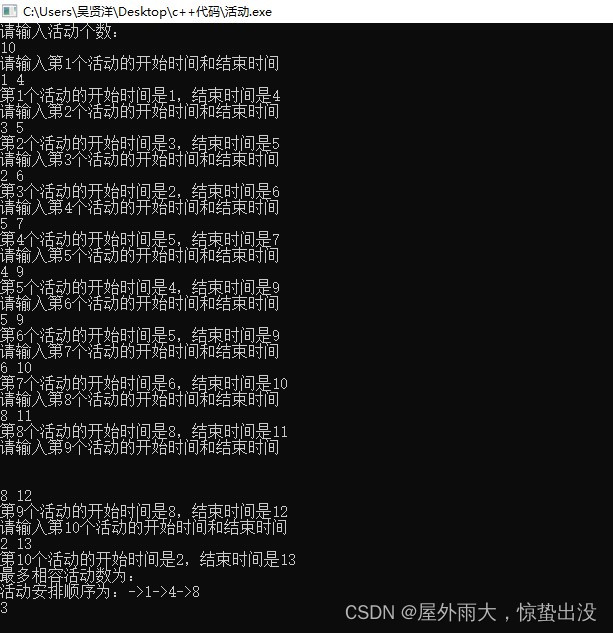
关键步骤证明:

时间复杂度与空间复杂度:
时间复杂度主要为排序花的时间为0(
),如果换成其他排序可以降低时间复杂度,空间复杂度为0(n)
(3)最小生成树--prim算法实现
问题描述:
给定一个图,求出其最小生成树
最小生成树定义
对于一个带权(假定每条边上的权值均为大于零的实数)连通无向图G中的不同生成树,各树的边上的权值之和可能不同;图中所有生成树中具有边上的权值之和最小的树称为该图的最小生成树.按照生成树的定义,n个顶点的连通图的生成树有n个顶点和(n-1)条边.因此构造最小生成树的准则有三条:
(1) 必须只使用该图中的边来构造最小生成树;
(2) 必须使用且仅使用(n-1)条边来连接图中的n个顶点;
(3) 不能使用产生回路的边.
思路与关键点:
首先,这里有一个头文件<alogrithmn>,里面包含了丰富实用的函数,非常nice。这里使用到了其中的fill函数和min函数。分别用来填充数组和求最小值的。建立一个数组used,记录哪些没有进入最小生成树的集合,每次不断地将没有加入used中的距离加入used数组的节点 权值最小的节点加入used数组。 更新V轮mincost数组,得到最小生成树。
伪代码:

代码:
#include<iostream>
#include<algorithm>
#define MAX_V 100
#define INF 1000
using namespace std;
int main()
{
int V,E;
int i,j,m,n;
int cost[MAX_V][MAX_V];//存储每个节点之间的权值
int mincost[MAX_V];//记录那些已经进入最小生成树的节点之间的权值
bool used[MAX_V];//用于判断是否已经进入最小生成树,false表示否,true表示是
printf("请输入节点个数与边数\n");
cin>>V>>E;
int Trace[V];
fill(mincost,mincost+V+1,INF);//最小生成树一共有V个节点,V+1条边
fill(used,used+V,false);//一共有V个节点
//初始化cost[]
for(i=0;i<V;i++)
{
for(j=0;j<V;j++)
{
if(i==j) cost[i][j]=0;//节点自己到自己权值为0
else cost[i][j]=INF;
}
}
//向cost[]里面填充各个节点之间的权值
for(m=0;m<E;m++)
{
printf("请输入两个端点以及它们之间边的权值\n");
cin>>i>>j>>cost[i][j];
cost[j][i]=cost[i][j];//无向图,中心对称
}
mincost[0]=0;
int res=0;//存储最终的最小生成树权值和
int count=0;
/*遍历图,不断地将没有加入used中的距离加入used数组的节点
权值最小的节点加入used数组。
更新V轮mincost数组,得到最小生成树。
*/
while(true)//也可以写成for(int i=0;i<V;i++)
{
int v=V;
for(m=0;m<V;m++)
{
if((!used[m])&&(mincost[m]<mincost[v]))
v=m;
}
Trace[count]=v;
count++;
if(v==V) break;
Trace[count]=v;//最后一个跳出来了,没记录,要把最后一个节点加入
used[v]=true;
res+=mincost[v];
for(m=0;m<V;m++)
{/*取(新加入最小生成树的节点到其他节点的权值)和
记录在mincost中的到其他节点的权值进行比较,
取它们之间的最小值,来更新mincost数组*/
mincost[m]=min(mincost[m],cost[v][m]);
}
}
printf("最小生成树权值是:\n");
cout<<res<<endl;
printf("依次找到的节点是:\n");
for(int i=0;i<V;i++){
cout<<"->"<<Trace[i];
}
cout<<endl;
}运行结果:
输入上面单源点最短路径所示的图,运行结果如下
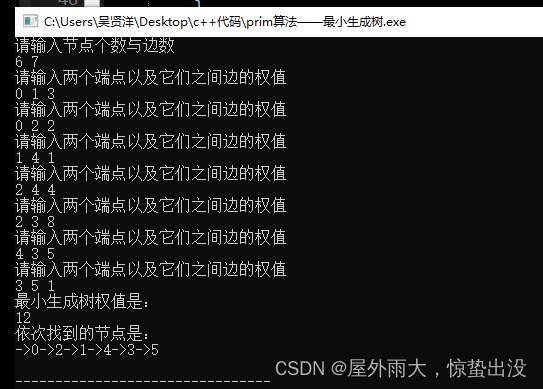
关键步骤证明:
视频证明
时间复杂度与空间复杂度:
时间复杂度与空间复杂度都是0()


![[图解]产品经理创新模式03封装领域逻辑](https://img-blog.csdnimg.cn/direct/e071c8fa03074f06b4bf1f4da10c114a.png)