1. 二分查找的概念

折半查找(BinarySearch)技术，又称为二分查找。它的前提是线性表中的记录
必须是关键码有序(通常从小到大有序)，线性表必须采用顺序存储。

折半查找的基本思想是:在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功; 若给定值小于中间记录的关键字，则在中间记录的左半区继续查找;若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直
到查找成功，或所有查找区域无记录，查找失败为止。

2. 整数的二分

二分的本质：根据一定的条件或性质(一般是与答案之间的关系)，可以将查找的区间分为两部分，然后对中间值mid进行判断，确定答案在mid的左侧还是右侧，以此来缩小查找的范围。

核心：保证答案在更新后的区间，当区间长度为1时我们就找到了答案。

二分查找是有两个模版的，根据这两个模版我们能够解决几乎全部的二分查找问题。

2.1 二分的模版一

int main()
{
	int L = 0;
	int R = length - 1; //length为数组的长度

	while (L < R)
	{
		int mid = L + R + 1 >> 1;
		if (check(mid)) //检查mid指向的元素在答案所分的两个区间的哪一侧
			L = mid;
		else
			R = mid - 1;
	}
	return 0;
}

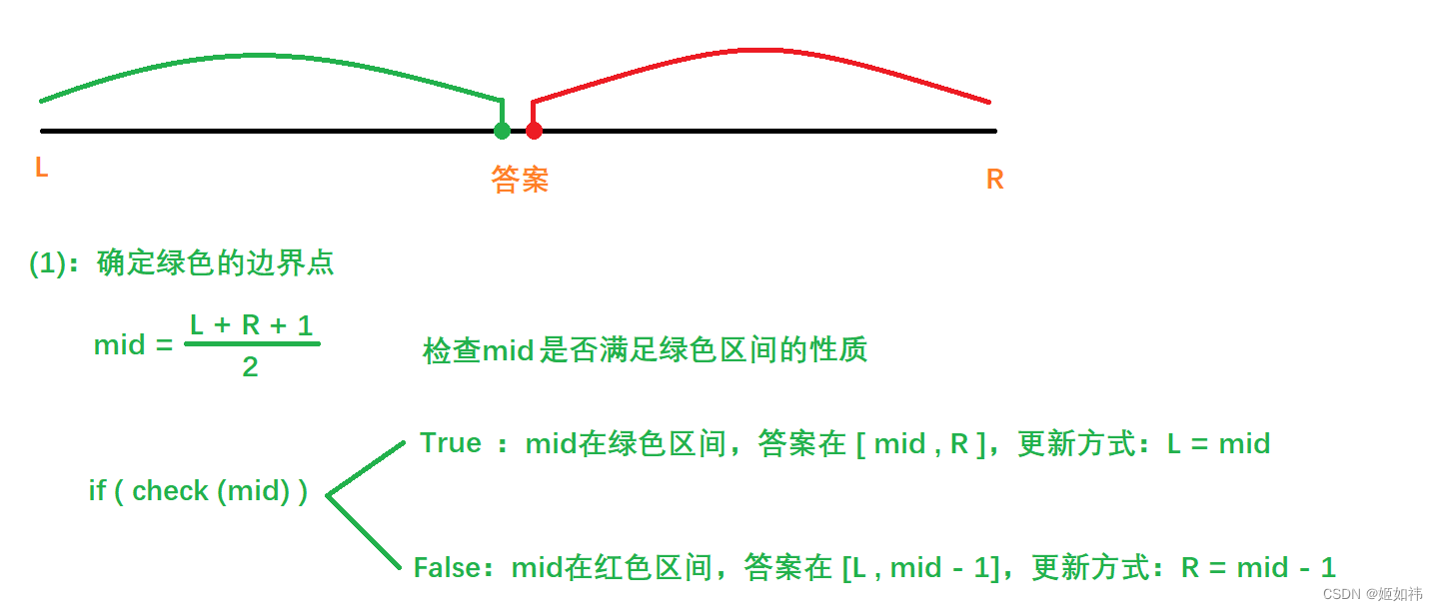
上图中，假设我们要确定的是绿色的点，在绿色区间的元素满足一定的条件，红色区间的元素也满足一定的条件(这两个区间的条件就是根据答案来确定的，后面有例题可以帮助大家理解)，然后我们求出mid所在的区间，假设mid满足绿色区间的条件，那么答案（要确定的绿色的点）肯定在mid的右侧，并且mid也可能是答案，所以答案在 [ mid, R ], 更新方式为： L = mid；当mid不满足绿色区间的性质，那么mid就满足红色区间的性质，此时mid不可能是答案（要确定的绿色的点），所以答案就在 [ L, mid - 1 ] 的区间内，更新区间的方式：R = mid - 1。

为什么mid = L + R + 1 >> 1???，这是由我们更新区间的方式决定了的，我们假设 L = R - 1时，如果按照 mid = L + R >> 1 来算，那么 mid = L + L + 1 >> 2 = L，我们发现 mid = L，然后更新区间 L = mid，即是 L = L，区间并没有变化，就会陷入死循环。由此，当更新区间的方式为：L = mid，R = mid - 1 时计算 mid 的方式为：mid = L + R + 1 >> 1。

2.2 二分的模版二


int main()
{
	int L = 0;
	int R = length - 1; //length为数组的长度

	while (L < R)
	{
		int mid = L + R >> 1;
		if (check(mid)) //检查mid指向的元素在答案所分的两个区间的哪一侧
			L = mid + 1;
		else
			R = mid;
	}
	return 0;
}

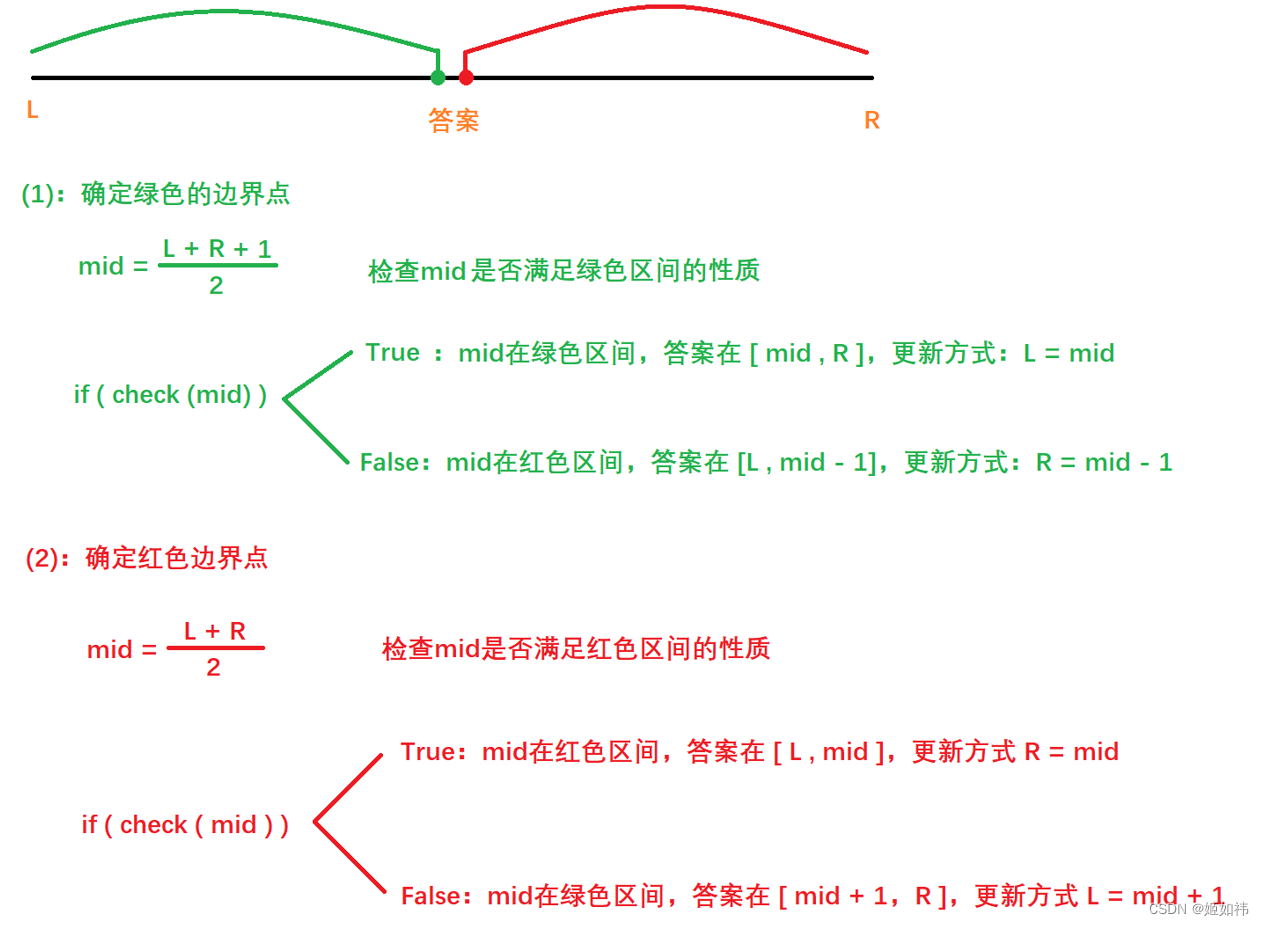
上图中，假设我们要确定的是红色的边界点，我们求出mid，检查mid是否满足红色区间的条件，如果满足，则mid在红色区间，并且mid可能是答案，所以答案(要确定的红色点的下标) 在 [L, mid ]区间内，更新方式 R = mid，同理当mid不满足红色区间的条件，答案就在 [ mid + 1, R ] 的区间内，更新区间的方式为：L = mid + 1。

2.3. 案例剖析

原题链接：

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

题目描述：

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

思路分析：

我们只需要进行两次二分查找，找到第一个target的下标和最后一个target位置的下标即可。

很据上面的基础知识，来分析此题：

(1)：找第一个 target 的下标。非递减序列，第一个 target 将整个序列分为两部分，后面区间的元素满足 >= target 的条件，如果 mid 满足 >= target 的条件那么mid 就在后面的区间，并且mid可能是第一个target(条件是 >= target嘛)，所以答案就在 [ L, mid ]，更新方式为 R = mid，一旦我们确定了更新方式就知道了该用哪一个模板，显然就是模板二。然后就只需要套模板就行。

(2)：找最后一个 target 的下标。非递减序列，最后一个 target 将整个序列分为两部分，前面区间的元素满足 <= target 的条件，如果 mid 满足 <= target 的条件那么mid 就在前面的区间，并且mid可能是最后一个target(条件是 <= target嘛)，所以答案就在 [ mid, R ]，更新方式为 L = mid，一旦我们确定了更新方式就知道了该用哪一个模板，显然就是模板一。然后就只需要套模板就行。

循环结束时 L = R 的最后返回 L 或则 R 都行，前提是 target 存在哈。

int* searchRange(int* nums, int numsSize, int target, int* returnSize){
    //放结果的数组
    int* array = (int*)malloc(sizeof(int) * 2);
    //返回的数组大小都是2
    *returnSize = 2;
    //如果是空的数组，返回两个-1
    if(numsSize == 0)
    {
        array[0] = -1;
        array[1] = -1;
        return array;
    }
    //找第一个target
    int L = 0, R = numsSize - 1;
    while(L < R)
    {
        //模板二
        int mid = L + R >> 1;
        if(nums[mid] >= target)
            R = mid;
        else
            L = mid + 1;
    }
    //如果找不到target，返回两个-1
    if(nums[L] != target)
    {
        array[0] = -1;
        array[1] = -1;
        return array;
    }
    //保存结果
    array[0] = L;
    //找第二个target
    L = 0;
    R = numsSize - 1;
    while(L < R)
    {
        //模版一
        int mid = L + R + 1 >> 1;
        if(nums[mid] <= target)
            L = mid;
        else
            R = mid - 1;
    }
    //保存结果
    array[1] = L;
    return array;
}