1. 验证全响应
%验证全响应=零状态响应+零输入响应
%y(n)=4y(n-1)+x(n),其中x(n)=δ(n),y(-1)=2.
clc;%清屏
clear all;%清除所有变量的值
b=[1];
a=[1,-4];
ys=[2];
xs=[0];%没有初始值,就是0
xn=[1, zeros(1,4)];%输入序列,假设长度是5,则输出长度也是5
n=0:length(xn)-1;%序列横坐标
y0=filtic(b,a,ys,xs);%由初始状态得到的y0值,
yn1=filter(b,a,zeros(1, length(xn)), y0);%零输入响应,由y0递推可得。
yn2=filter(b,a,xn, 0);%零状态响应
yn=filter(b,a,xn, y0);%全响应结果:
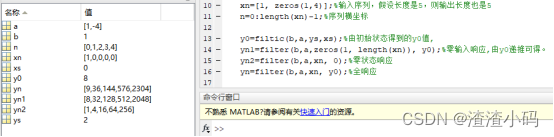
2. 验证系统的时不变
%验证时不变
%y(n)=4y(n-1)+x(n),其中x(n)=δ(n),y(-1)=0.
clc;%清屏
clear all;%清除所有变量的值
b=[1];
a=[1,-4];
ys=[0];
xs=[0];
xn=[1, zeros(1,4)];%输入序列,假设长度是5,则输出长度也是5
n=0:length(xn)-1;%序列横坐标
y0=filtic(b,a,ys,xs);%由初始状态得到的y0值,
yn1=filter(b,a,zeros(1, length(xn)), y0);%零输入响应,由y0递推可得。
yn2=filter(b,a,xn, 0);%零状态响应
yn=filter(b,a,xn, y0);%全响应
%验证差分方程的时变特性
xn_d=[0,1,0,0,0];
yn_d=filter(b, a, xn_d, y0);结果:只有初始状态为0的情况下才是时不变的
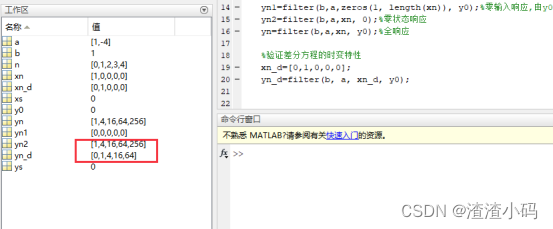
如果初始值不为0,结果是不一样的:
%验证时不变
%y(n)=4y(n-1)+x(n),其中x(n)=δ(n),y(-1)=2,初始值不为0
clc;%清屏
clear all;%清除所有变量的值
b=[1];
a=[1,-4];
ys=[2];%初始值
xs=[0];
xn=[1, zeros(1,4)];%输入序列,假设长度是5,则输出长度也是5
n=0:length(xn)-1;%序列横坐标
y0=filtic(b,a,ys,xs);%由初始状态得到的y0值,
yn1=filter(b,a,zeros(1, length(xn)), y0);%零输入响应,由y0递推可得。
yn2=filter(b,a,xn, 0);%零状态响应
yn=filter(b,a,xn, y0);%全响应
%验证差分方程的时变特性
xn_d=[0,1,0,0,0];
yn_d=filter(b, a, xn_d, y0);结果:

3. 验证系统的稳定性
%求系统函数h(n), 并验证该系统是否是稳定的
%y(n)-2y(n-1)=x(n)
clc;%清屏
clear all; %清除所有变量的值
b=[1]; %差分方程系数
a=[1,-2]; %差分方程系数
N=100; %序列长度
dn=[1, zeros(1,N-1)]; %产生单位脉冲序列
hn=filter(b,a,dn); %求单位脉冲响应h(n),没有初始状态,直接输入即可
n=0:N-1;
xn=ones(1,N);%输入是单位阶跃序列
yn=filter(b,a,xn);%求系统输出
subplot(211);
stem(n, hn);title('h(n)');
subplot(212);
stem(n, yn);title('输入是x(n)=u(n)');结果:
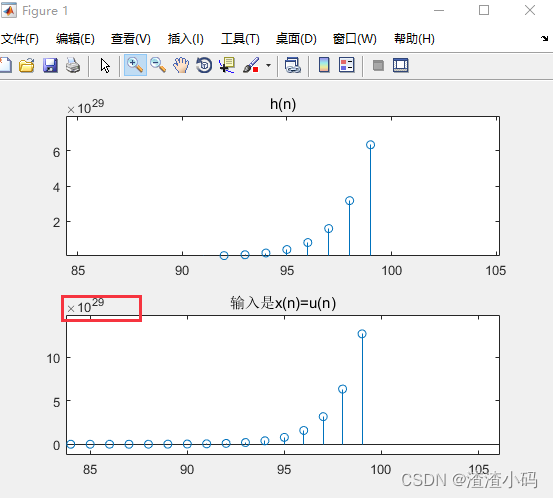
可以发现,输入有界,但输出并不是有界的,该系统不稳定,实际上h(n)是不收敛的序列。
4. 卷积法和递推法求系统输出
%卷积法和递推法有何差异
%y(n)=x(n)+2x(n-1)+4x(n-3), x(n)=[1 2 3 4]
clc;%清屏
clear all; %清除所有变量的值
b=[1 2 0 4]; %h(n)
a=[1]; %差分方程系数
xn=1:4; %输入序列
yn_cov=conv(b,xn);%卷积法求系统输出
yn_filter=filter(b, a, xn);%递推法求系统输出结果:

长度不同,卷积法结果的长度是:4+4-1,而递推法的输出和输入长度相同。可以在递推法的输入序列后补上三个0,得到的结果就是一样的:









![[Redis]基本全局命令](https://img-blog.csdnimg.cn/direct/fc696efe75cf451ebacbb1675bb82c86.png)

![c语言:利用随机函数产生20个[120, 834] 之间互不相等的随机数, 并利用选择排序法将其从小到大排序后输出(每行输出5个)](https://img-blog.csdnimg.cn/direct/6cfdce68f41d4cb1971a3175f31e3742.png)


![[STM32-HAL库]Flash库-HAL库-复杂数据读写-STM32CUBEMX开发-HAL库开发系列-主控STM32F103C6T6](https://img-blog.csdnimg.cn/direct/db1f0cc36a25422087ab111766224fe1.png)