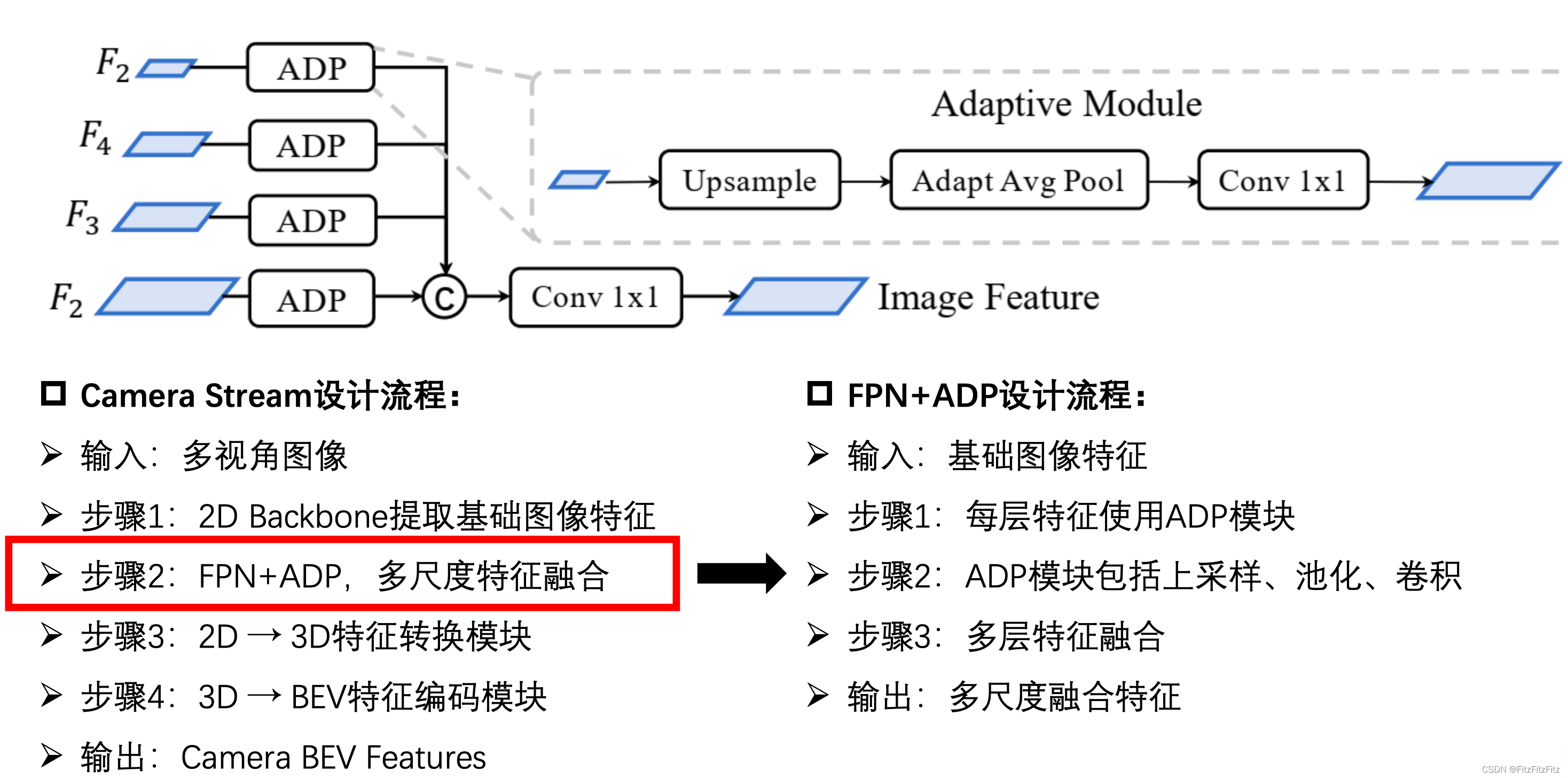
简介
在Kettle(也称为Pentaho Data Integration,PDI)中,Switch/Case 是一个关键的组件,用于根据特定条件将数据流分支到不同的路径。Switch组件评估输入数据中的某个字段,并将数据标记后传递给相应的Case组件,每个Case组件根据配置的条件处理匹配的数据。这种机制不仅使得数据处理流程更为清晰和灵活,还能有效简化复杂的逻辑操作,使得数据集成和管理更为高效和易于维护。
使用
场景
如果 行流数据 isSave 为 1 则 入库 否则不做任何处理
拖拽核心对象到面板

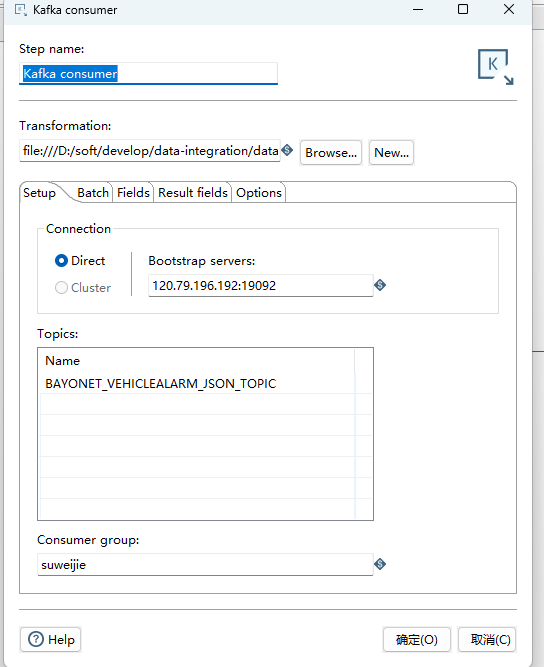
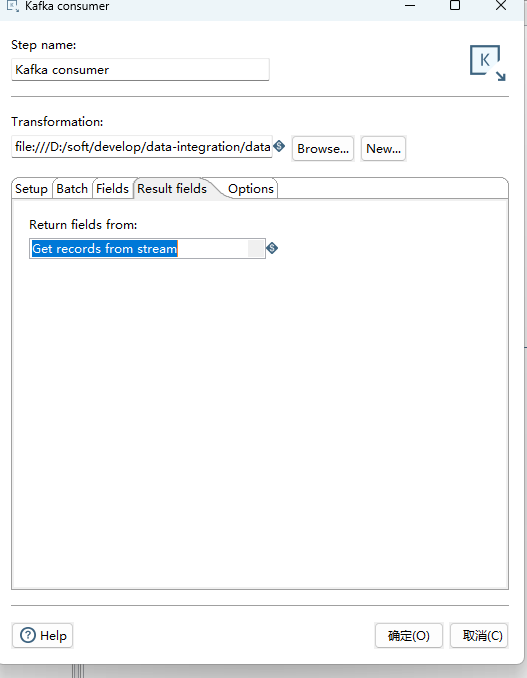
Kafka consumer 对应的配置
JSON input 的配置


表输出的配置

配置Switch / case

调试
运行转换
使用idea发送一条消息到监听的Kafka主题

isSave 为 1的时候
可以看到表输出有一条 out 数据
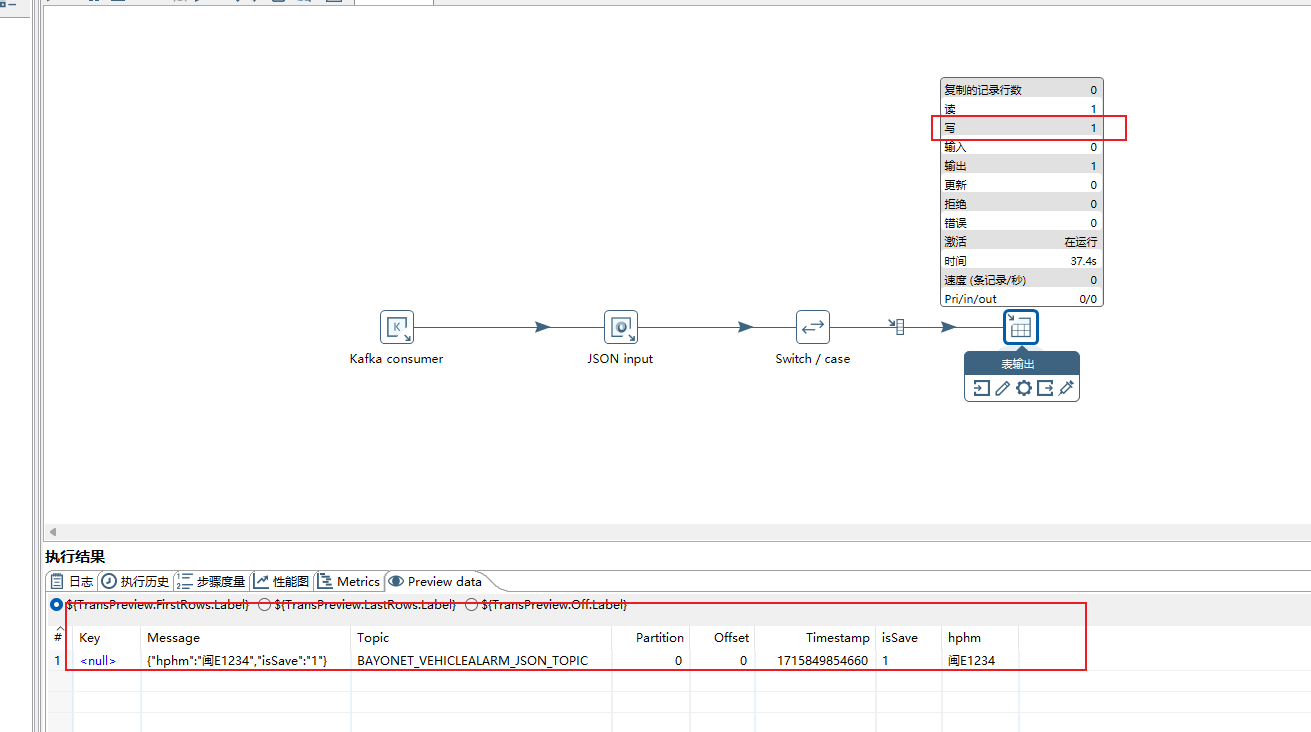
isSave 为 0的时候
这时候数据应该是俩条而已,可以看到 Switch / case 有俩条数据,表输出没有增加数据


然后可以看到数据库也是只有一条数据