719. 找出第 K 小的数对距离 - 力扣（LeetCode）

数对 (a,b) 由整数 a 和 b 组成，其数对距离定义为 a 和 b 的绝对差值。

给你一个整数数组 nums 和一个整数 k ，数对由 nums[i] 和 nums[j] 组成且满足 0 <= i < j < nums.length 。返回 所有数对距离中 第 k 小的数对距离。

示例 1：

输入：nums = [1,3,1], k = 1 输出：0 解释：数对和对应的距离如下： (1,3) -> 2 (1,1) -> 0 (3,1) -> 2 距离第 1 小的数对是 (1,1) ，距离为 0 。

示例 2：

输入：nums = [1,1,1], k = 2 输出：0

示例 3：

输入：nums = [1,6,1], k = 3 输出：5

提示：

• n == nums.length

• 2 <= n <= 10(4)

• 0 <= nums[i] <= 10(6)

• 1 <= k <= n * (n - 1) / 2

方法1,二分答案法,没有剪枝

1.

nums数组中的数对组合,下标分别为<0,1>,<0,2>...<0,n-1>

<1,2>,<1,3>....<1,n-1>

....

<n-2,n-1>

一共有n-1+n-2+....+1=((n-1)+1)*(n-1)/2=(n-1)*n/2对数对.

对于每一个数对,差值的绝对值,可以发现排序之后不会影响数组组合和结果.

我们需要找到所有数对距离从大到小排序之后的第k小的数对距离.

2.

将所有的数对距离排序之后,找到第k小的数对距离.

我们需要找一个数对距离的值,这个值是第k小的数对距离.

如果固定数对距离,可以求得他是第几小的数对距离,只需要求得小于等于limit的数对距离有多少个就知道这是第几小的数对距离.

用二分法找数对距离,判断数对距离是否是第k小的数对距离.

f(limit)函数返回小于等于limit数对距离的个数.如果小于k,说明数对距离不可能是答案.[0,limit]都不可能是答案.

去右边找答案.

如果是大于等于k,说明可能是答案,ret记录下来,去左边找可能的答案.

class Solution {
public:
    /*
    数对距离,二元组,排序和不排序不影响答案.
    数组n个元素,对应的数对个数是1+2+...+n-1=(1+n-1)*(n-1)/2=n*(n-1)/2
    分别下标对应<0,1><0,2>...<0,n-1>====> n-1
    <1,2>...<1,n-1>=====> n-2
    ...
    <n-2,n-1>=====> 1

    数对距离的可能范围[0,num_max-nums_min]
    数对距离排序之后第k个,是我们要找的值

    数对距离排序后第k个数对距离是答案.
    二分答案法,f(limit)数对距离大于等于limit的个数.
    二分答案法,固定答案判断其他条件,更方便
    1,2,3,4,5,6
    */

    vector<int> arr; // 保存输入的数组
    int k; // 第 k 小的数对距离
    int n; // 数组长度
    int ret; // 保存结果，即第 k 小的数对距离

    // 判断在给定的限制下，数对距离小于等于 limit 的个数是否大于等于 k
    bool f(int limit) {
        int count = 0; // 满足条件的数对个数
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (arr[j] - arr[i] <= limit) {
                    count++;
                } else {
                    break;
                }
            }
        }
        return count >= k;
    }

    // 初始化函数，计算数组长度并排序
    void init() {
        n = 0, ret = 0;
        sort(arr.begin(), arr.end());
        n = arr.size();
    }

    // 二分查找解决问题
    void solve() {
        int l = 0, r = arr[n - 1] - arr[0]; // 定义二分查找的左右边界
        while (l <= r) {
            int mid = l + ((r - l) >> 1); // 计算中间值
            if (f(mid)) { // 如果在当前限制下满足条件的数对个数大于等于 k
                ret = mid; // 更新结果
                r = mid - 1; // 缩小右边界
            } else {
                l = mid + 1; // 增大左边界
            }
        }
    }

    // 主函数，计算第 k 小的数对距离
    int smallestDistancePair(vector<int>& _nums, int _k) {
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出
        arr = _nums, k = _k;
        init(); // 调用初始化函数
        solve(); // 调用二分查找解决问题
        return ret; // 返回结果
    }
};

方法2,二分答案法,剪枝

1.

找小于等于limit的个数是否大于等于k.

这个过程j可以不用回退.

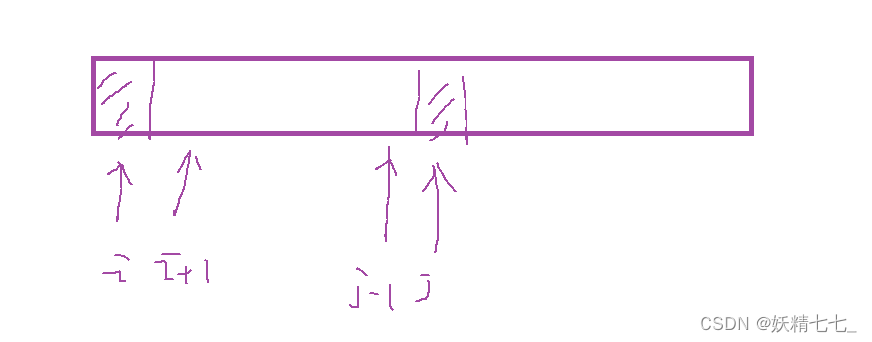
i和i+1~j-1数对距离都小于等于limit,但是i和j数对距离大于limit,那么i+1和i+1~j-1的数对距离也以一定小于等于limit.

所以j不需要回退,直接加上当前位置和j之间的个数.

如果ij相等j需要++.

class Solution {
public:
    /*
    数对距离,二元组,排序和不排序不影响答案.
    数组n个元素,对应的数对个数是1+2+...+n-1=(1+n-1)*(n-1)/2=n*(n-1)/2
    分别下标对应<0,1><0,2>...<0,n-1>====> n-1
    <1,2>...<1,n-1>=====> n-2
    ...
    <n-2,n-1>=====> 1

    数对距离的可能范围[0,num_max-nums_min]
    数对距离排序之后第k个,是我们要找的值

    数对距离排序后第k个数对距离是答案.
    二分答案法,f(limit)数对距离大于等于limit的个数.
    二分答案法,固定答案判断其他条件,更方便
    1,2,3,4,5,6

    */

    vector<int> arr;
    int k;
    int n;
    int ret;
    
    bool f(int limit) {// 判断在给定的限制下，数对距离小于等于 limit 的个数是否大于等于 k
        int count = 0;
        int j = 1;
        for (int i = 0; i < n; i++) {
            if (i == j)
                j++;
            count += j - i - 1;
            for (; j < n; j++) {//剪枝不回退
                if (arr[j] - arr[i] <= limit) {
                    count++;
                } else {
                    break;
                }
            }
        }
        return count >= k;
    }
    void init() {
        n = 0, ret = 0;

        sort(arr.begin(), arr.end());
        n = arr.size();
    }
    void solve() {
        int l = 0, r = arr[n - 1] - arr[0];
        while (l <= r) {
            int mid = l + ((r - l) >> 1);//位运算一定要加括号
            if (f(mid)) {
                ret = mid;
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
    }

    int smallestDistancePair(vector<int>& _nums, int _k) {
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
        arr = _nums, k = _k;
        init();
        solve();
        return ret;
    }
};

N 台电脑的最长时间 - 力扣（LeetCode）

你有 n 台电脑。给你整数 n 和一个下标从 0 开始的整数数组 batteries ，其中第 i 个电池可以让一台电脑 运行 batteries[i] 分钟。你想使用这些电池让 全部 n 台电脑 同时 运行。

一开始，你可以给每台电脑连接 至多一个电池 。然后在任意整数时刻，你都可以将一台电脑与它的电池断开连接，并连接另一个电池，你可以进行这个操作 任意次 。新连接的电池可以是一个全新的电池，也可以是别的电脑用过的电池。断开连接和连接新的电池不会花费任何时间。

注意，你不能给电池充电。

请你返回你可以让 n 台电脑同时运行的 最长 分钟数。

示例 1：

输入：n = 2, batteries = [3,3,3] 输出：4 解释： 一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 1 连接。 2 分钟后，将第二台电脑与电池 1 断开连接，并连接电池 2 。注意，电池 0 还可以供电 1 分钟。 在第 3 分钟结尾，你需要将第一台电脑与电池 0 断开连接，然后连接电池 1 。 在第 4 分钟结尾，电池 1 也被耗尽，第一台电脑无法继续运行。 我们最多能同时让两台电脑同时运行 4 分钟，所以我们返回 4 。

示例 2：

输入：n = 2, batteries = [1,1,1,1] 输出：2 解释： 一开始，将第一台电脑与电池 0 连接，第二台电脑与电池 2 连接。 一分钟后，电池 0 和电池 2 同时耗尽，所以你需要将它们断开连接，并将电池 1 和第一台电脑连接，电池 3 和第二台电脑连接。 1 分钟后，电池 1 和电池 3 也耗尽了，所以两台电脑都无法继续运行。 我们最多能让两台电脑同时运行 2 分钟，所以我们返回 2 。

提示：

• 1 <= n <= batteries.length <= 10(5)

• 1 <= batteries[i] <= 10(9)

1.

我们需要找运行时间,电池可以供电脑运行的最长的时间,我们找的这个时间一定有一个范围,0~所有时间累加和/n.

我们希望运行时间尽可能长.

f函数表示limit某一个特定的运行时间,电池是否可以供这些电脑运行这些时间.

如果不能说明limit这个运行时间短了,如果可以,再去更大的运行时间找,看看有没有更大的答案.

2.

f函数怎么判断这些电池能否供电脑运行这些时间,电池的电量如果大于等于limit,这个电池直接供一个电脑就可以了,如果电池电量小于limit说明,这个电池供完之后还需要其他的电池的帮助,这就是一个电池累加和,和总需要的电量的匹配问题.

只需要保证这些电池的累加和大于等于我们需要的电量即可.

所以我们需要将电量小于limit的电量累加,电脑数减去电量大于等于limit的个数,这个数乘以limit.

看累加电量是否大于等于n*limit.

3.

可以统一操作,如果不对n这个数进行修改,还原回去,左边就需要加上等量的值.也就是limit*(电量大于等于limit的个数).只需要电量大于等于limit的值加limit即可.

class Solution {
public:
    #define LL long long // 定义长整型别名

    int n; // 电脑的数量
    vector<int> arr; // 电池的电量数组
    LL ret; // 记录最长运行时间
    LL sum; // 电池电量总和

    // 判断在给定限制时间limit下，电池能否支持所有电脑运行
    bool f(LL limit) {
        LL totalTime = 0; // 记录总共供电时间
        for (int i = 0; i < arr.size(); ++i) {
            // 如果电池电量大于等于限制时间，则加上限制时间；否则，加上电池电量
            totalTime += arr[i] >= limit ? limit : arr[i];
            // 如果总供电时间大于等于限制时间乘以电脑数量，返回true
            if (totalTime >= limit * n) {
                return true;
            }
        }
        return false; // 如果无法满足条件，返回false
    }

    // 初始化，计算电池电量总和
    void init() {
        sum = accumulate(arr.begin(), arr.end(), 0LL);
    }

    // 二分查找解决最长运行时间
    void solve() {
        LL l = 0, r = sum / n; // 左边界为0，右边界为电池总电量除以电脑数量
        while (l <= r) {
            LL mid = l + ((r - l) >> 1); // 计算中间值
            // 如果在中间值限制下可以满足条件，更新结果，并尝试更长时间
            if (f(mid)) {
                ret = mid;
                l = mid + 1;
            } else { // 否则，尝试更短时间
                r = mid - 1;
            }
        }
    }

    // 主函数，计算最大运行时间
    long long maxRunTime(int _n, vector<int>& _batteries) {
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 加速输入输出
        n = _n; // 初始化电脑数量
        arr = _batteries; // 初始化电池数组
        init(); // 计算电池总电量
        solve(); // 二分查找计算最大运行时间
        return ret; // 返回结果
    }
};

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！