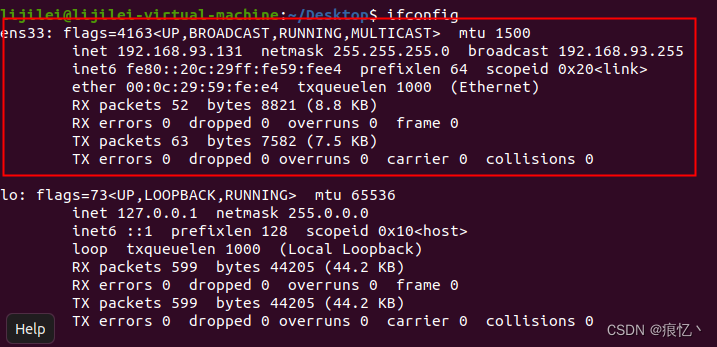
系统版本:windows server 2008 R2
问题-安装程序无法自动安装virtual machine…
在使用虚拟机安装windows server 2008 R2系统中,安装VMware Tools工具安祖啊寄给你失败,提示安装程序无法自动安装virtual machine…,必须手动安装
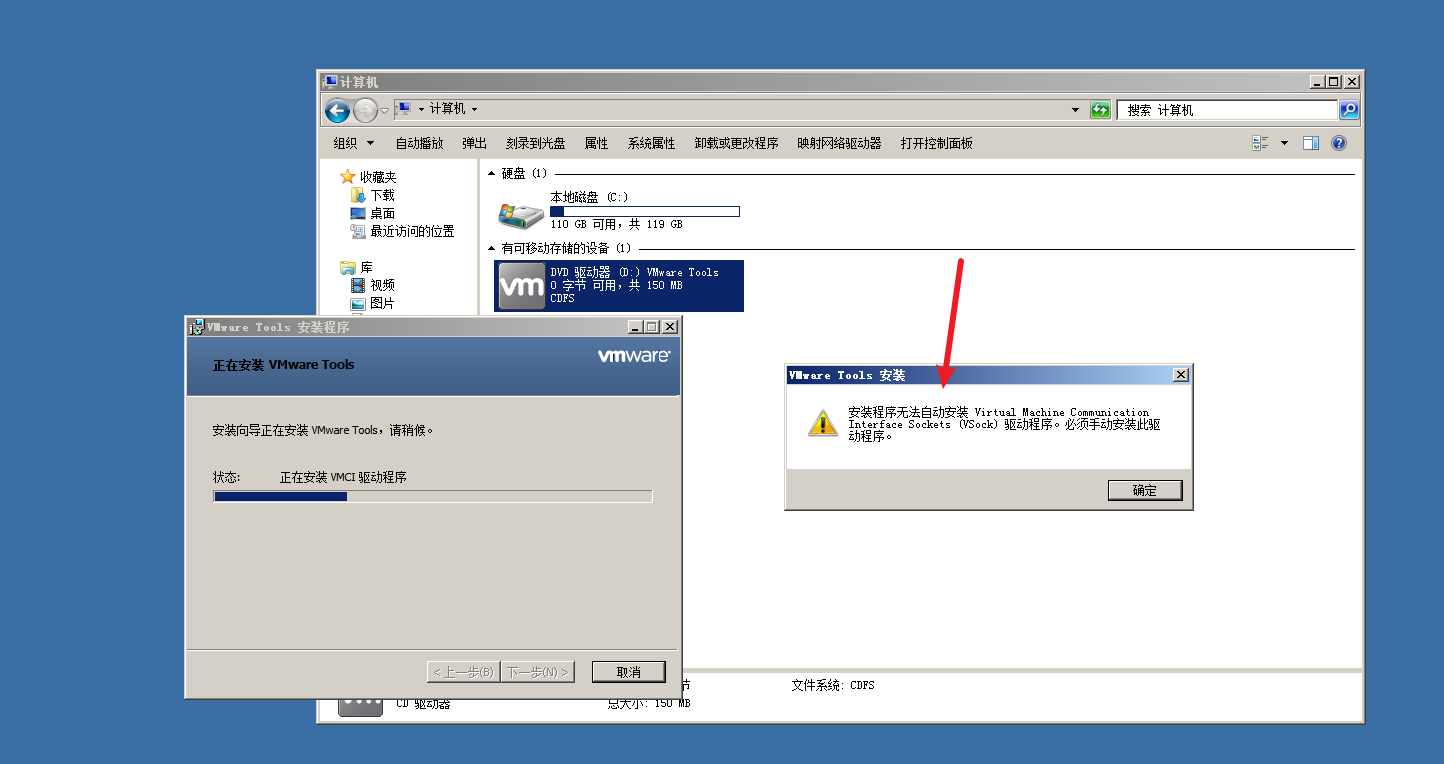
原因
官网的说明:https://knowledge.broadcom.com/external/article?legacyId=78708
官网是英文的,看不懂可以翻译


解决
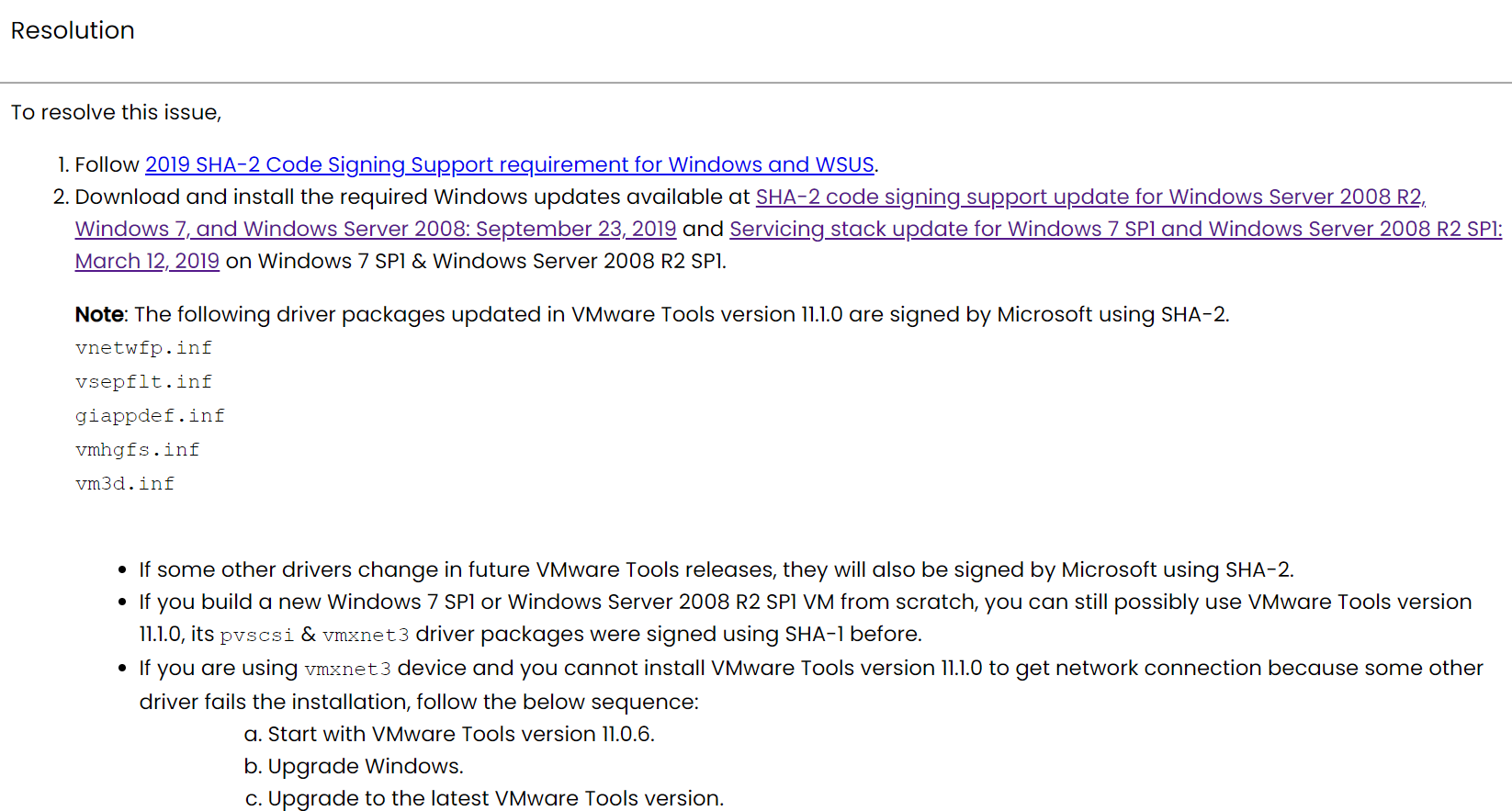
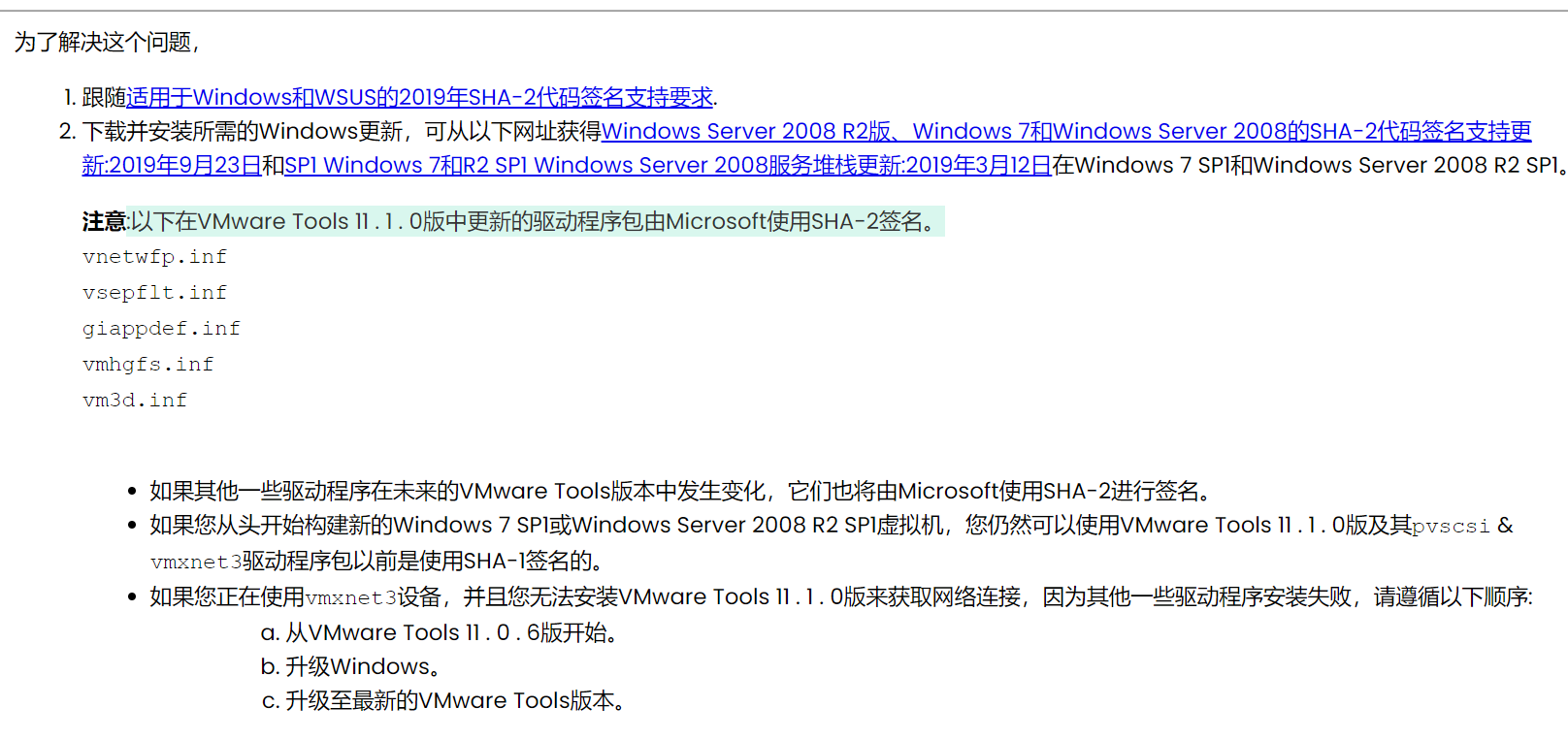
解决方法:安装相应的支持解决
由于是虚拟机中,在虚拟机外下载的话文件传不过去,这时候就要想办法解决了,远程桌面,通过优盘进行发送,或者直接在虚拟机中进行下载,目录共享等等方式
官网说明中已经给出了下载的连接可以直接打开,根据所给的提示进行安装
或者使用下面这个Microsoft Update Catalog地址下载
https://www.catalog.update.microsoft.com/search.aspx?q=kb4474419
下载
我的系统是windows server 2008 R2的,所以下载这个
点击后面的Download进行下载
搜索2019-09 Security Update for Windows Server 2008 R2 for x64-based Systems或对应的编号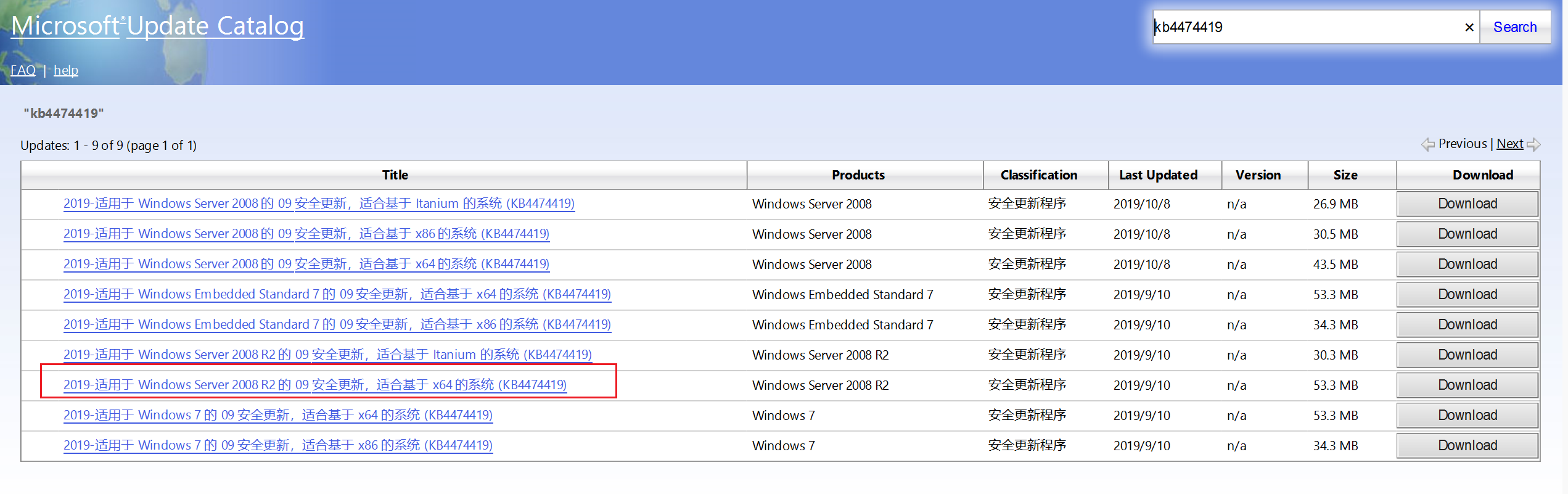
上传安装
上传
我这里使用文件共享
安装
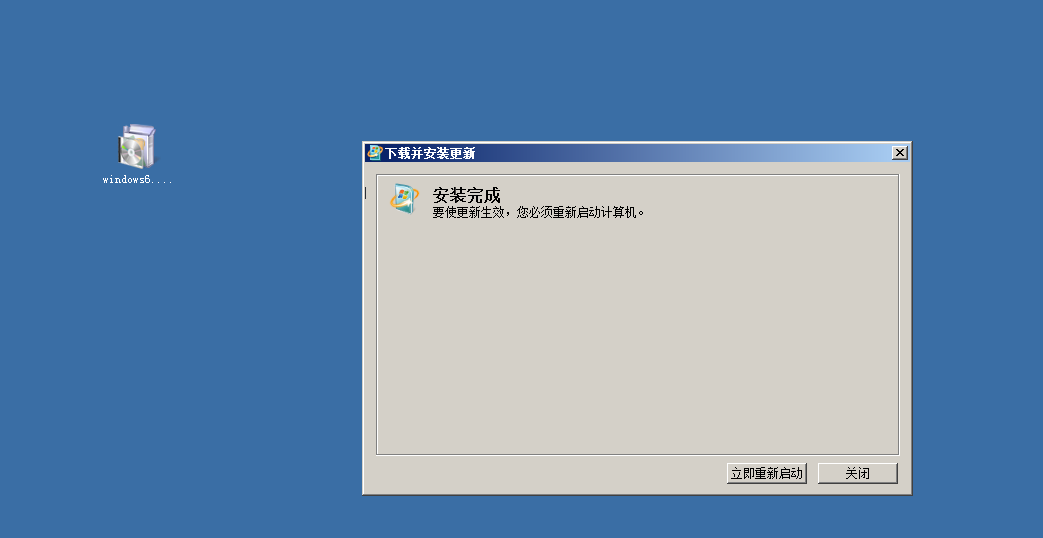
双击安装。根据提示直接下一步下一步就可以了
再次安装VMware Tools
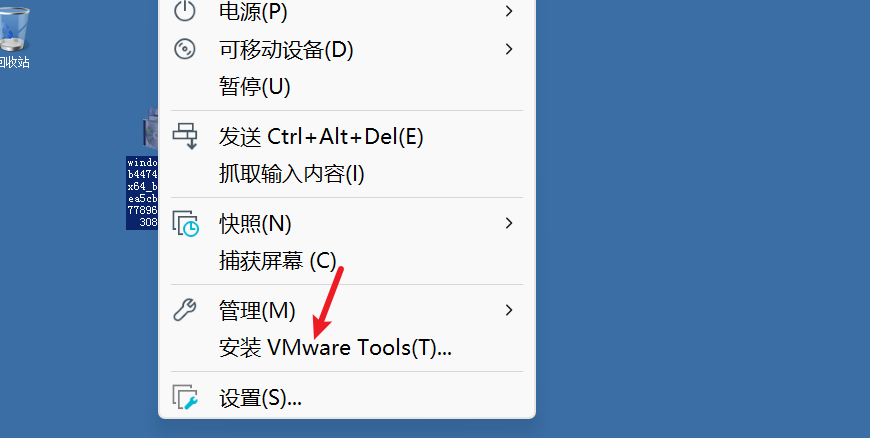
照常安装就可以了,安装过程不演示,最后可以正常安装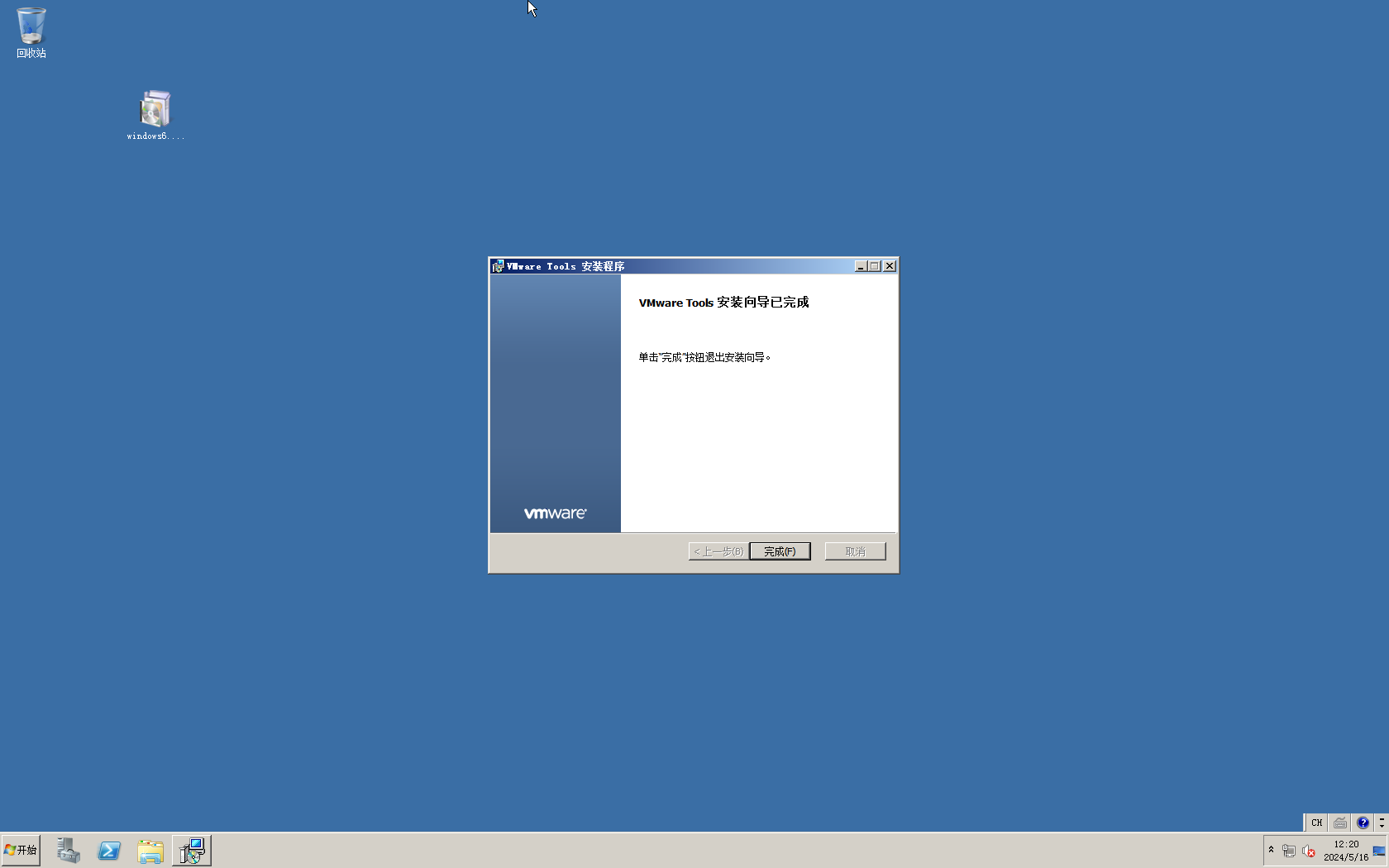
作者信息
作者:浅水鲤鱼qianshuiliyu
作者的平台
csdn:https://blog.csdn.net/qianshuiliyu
B站:https://space.bilibili.com/1571765231
作者邮箱:qianshuiliyu@qq.com