前言
更详细的在大佬的代码随想录 (programmercarl.com)
本系列仅是简洁版笔记,为了之后方便观看
本质
局部最优推出全局最优
验证
验证可不可以用贪心算法最好用的策略就是举反例,想不到反例就试贪心
分发饼干
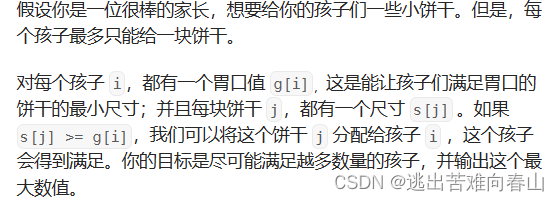
455. 分发饼干 - 力扣(LeetCode)
思考
1.贪心策略:大饼干满足大胃口/优先用小饼干
2.if语句的顺序不能变,如果变了,可能会抛异常
if (index >= 0 && s[index] >= g[i])3.for 控制胃口,for循环里面的if控制饼干,如果调换顺序,胃口可能持续不动
代码
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {//g是胃口,s是饼干
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int index=s.size()-1;
int result = 0;
for(int i=g.size()-1;i>=0;i--){
if(index>=0&&s[index]>=g[i]){
index--;
result++;
}
}
return result;
}
};摆动序列
376. 摆动序列 - 力扣(LeetCode)
思考
删掉单调坡上的元素,保留峰值元素
不需要陷入删除细节,只需要统计数组的峰值数量
情况
1.上下坡有平坡(从而在条件中添加prediff == 0 )
(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)2.首尾元素(数组中有两个元素的时候摆动也是2,可以看成延长前面的元素例如【1,0】变成【1,1,0】,从而转到情况1)
3.单调坡度有平坡(prediff只记录当摆动处出现时下一个坡的初始的坡度,这就是prediff=curdifff写在if语句里面跟着result变化的原因)
代码
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size()<=1) return nums.size();
int curDiff=0;//当前的差值
int preDiff=0;//之前的差值
int result=1;//序列默认序列最右边有一个峰值
for(int i=0;i<nums.size()-1;i++){
curDiff=nums[i+1]-nums[i];
if((preDiff<=0&&curDiff>0)||(preDiff >= 0 && curDiff < 0)){//峰值两侧符号不同
result++;
preDiff = curDiff;
}
}
return result;
}
};最大子序和
53. 最大子数组和 - 力扣(LeetCode)
局部最优:抛弃连续和是负数的情况
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int cnt=0;
for(int i=0;i<nums.size();i++){
cnt+=nums[i];
if(cnt>result){
result=cnt;
}
if(cnt<=0){
cnt=0;
}
}
return result;
}
};买卖股票最佳时机II
思路:
分解利润
第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
局部最优:只收获每天的正利润
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 1; i < prices.size(); i++) {
result += max(prices[i] - prices[i - 1], 0);
}
return result;
}
};跳跃游戏
关键:不是如何跳跃,而是覆盖范围,观察最后覆盖范围有没有到终点
cover = max(i + nums[i], cover)代码
class Solution {
public:
bool canJump(vector<int>& nums) {
int cover = 0;
if (nums.size() == 1) return true; //考虑特殊情况
for (int i = 0; i <= cover; i++) {
cover = max(i + nums[i], cover);
if (cover >= nums.size() - 1) return true; // 说明覆盖范围可以覆盖到终点
}
return false;
}
};