React 第三十七章 Scheduler 最小堆算法

news2025/4/27 17:43:51

在 Scheduler 中，使用最小堆的数据结构在对任务进行排序。

// 两个任务队列
var taskQueue: Array<Task> = []; 
var timerQueue: Array<Task> = [];

push(timerQueue, newTask); // 像数组中推入一个任务
pop(timerQueue); // 从数组中弹出一个任务
timer = peek(timerQueue); // 从数组中获取第一个任务

我们在学习 Scheduler 中最小堆算法之前，需要先了解什么是二叉堆。

二叉堆

二叉堆是一种基于完全二叉树的数据结构，它满足堆属性：对于每个节点x，x的父节点的值小于等于x的值（最小堆）或者大于等于x的值（最大堆）。

根据二叉堆的定义我们发现一个名次 完全二叉树。，完全二叉树是对二叉树、完全树的一种特殊情况。

下面我们来了解什么是二叉树和完全树

二叉树

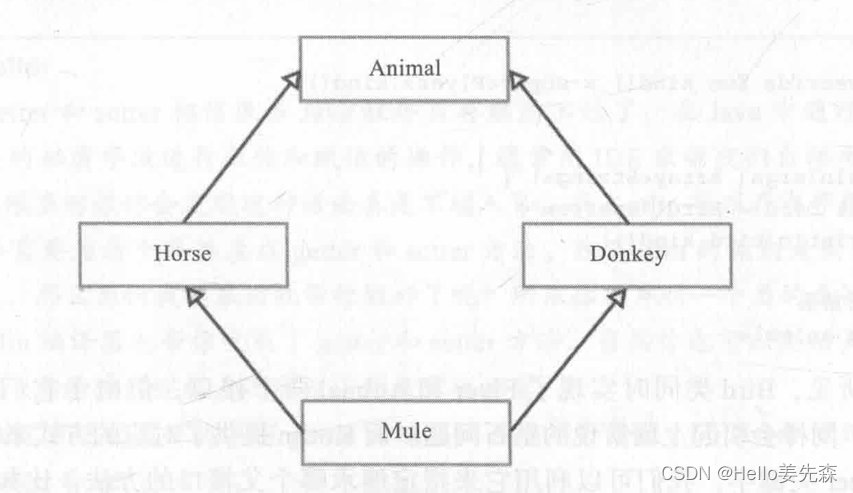
二叉树是一种特殊的树结构，它的每个节点最多有两个子节点，称为左子节点和右子节点。例如下图：

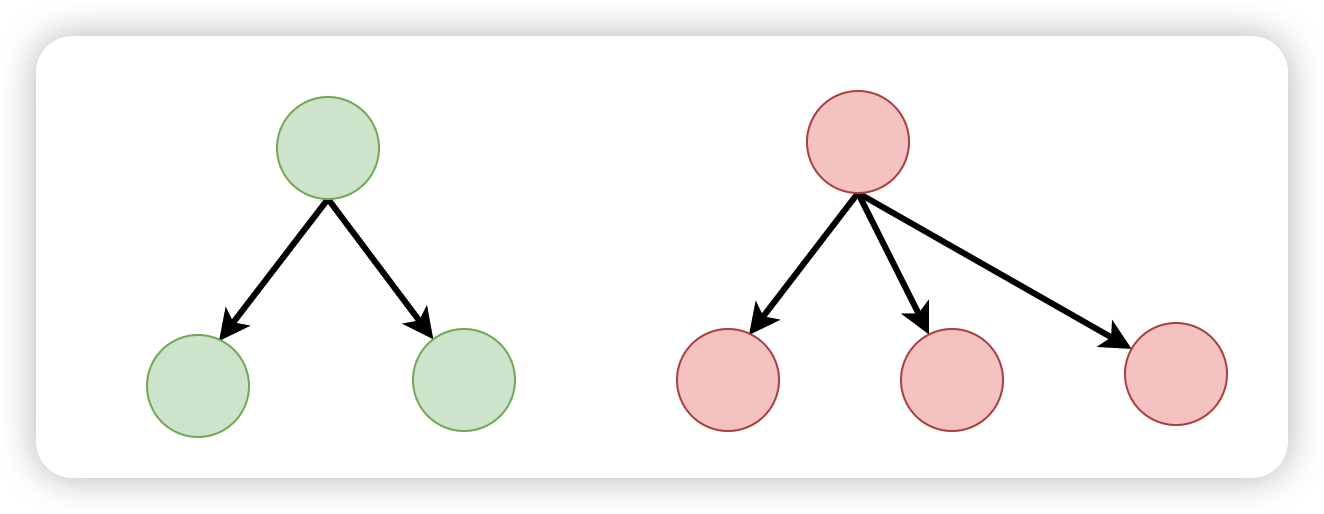
完全树

所谓完全树，指的是一棵树再进行填写的时候，遵循的是“从左往右，从上往下”

例如下面的这些树，就都是完全树：

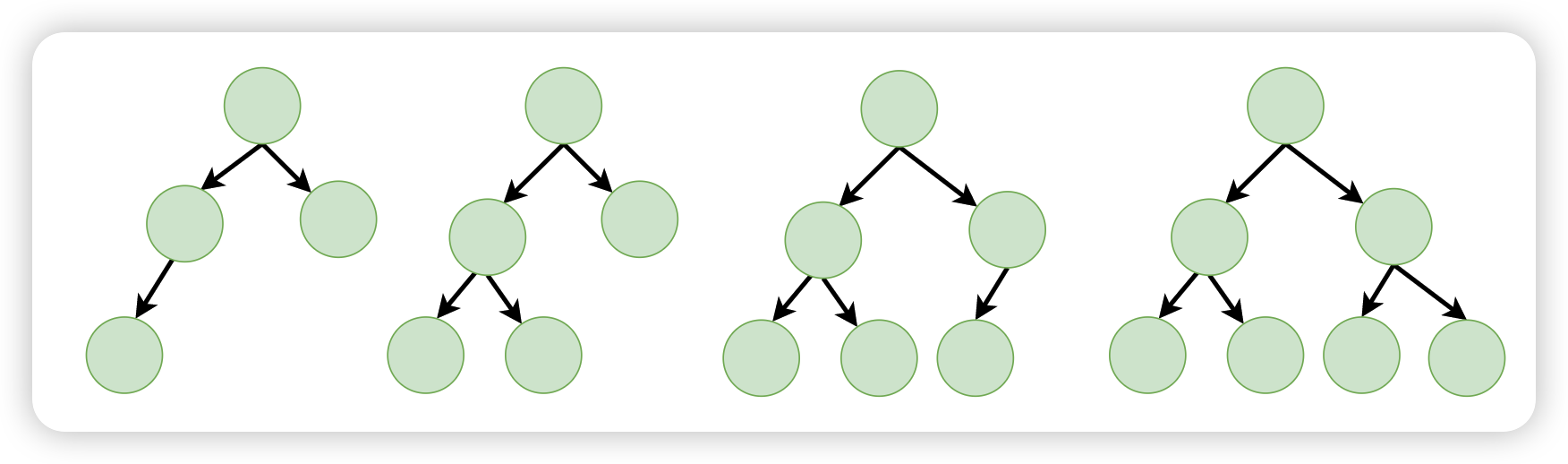
完全树中的数值

可以分为两大类：

最大堆：父节点的数值大于或者等于所有的子节点
最小堆：刚好相反，父节点的数值小于或者等于所有的子节点

最大堆示例：

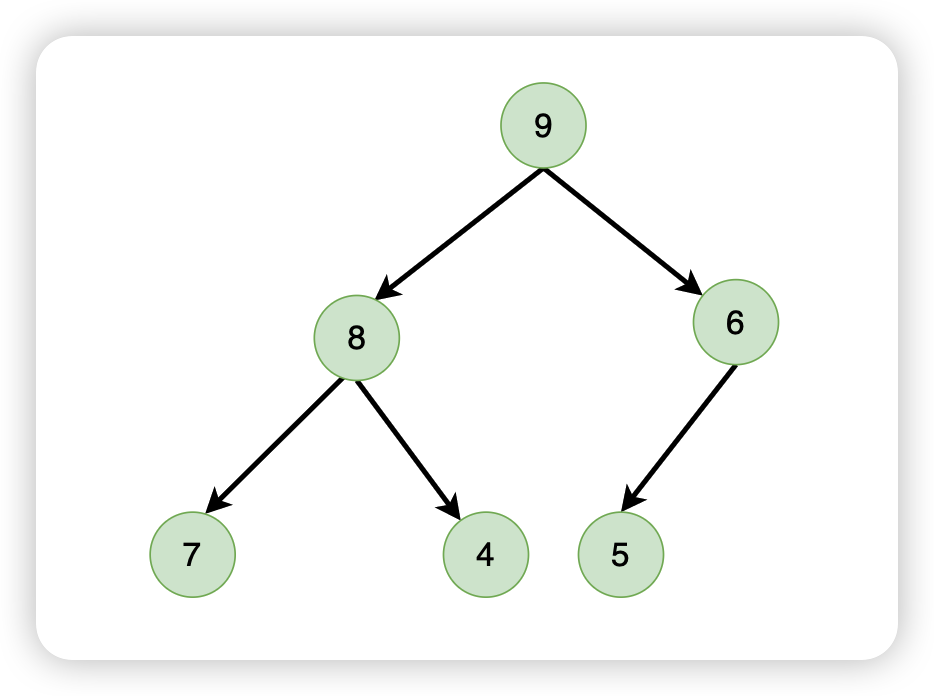
最小堆示例：

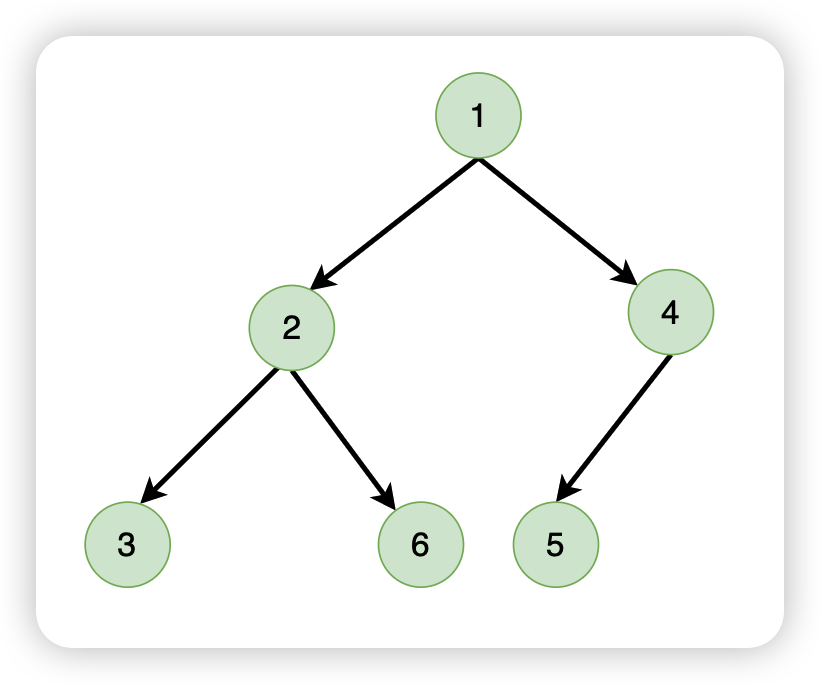
无论是最大堆还是最小堆，第一个节点一定是这个堆中最大的或者最小的
每一层不是按照一定顺序来排列的，比如下面的例子，6可以在左分支，3可以在右分支

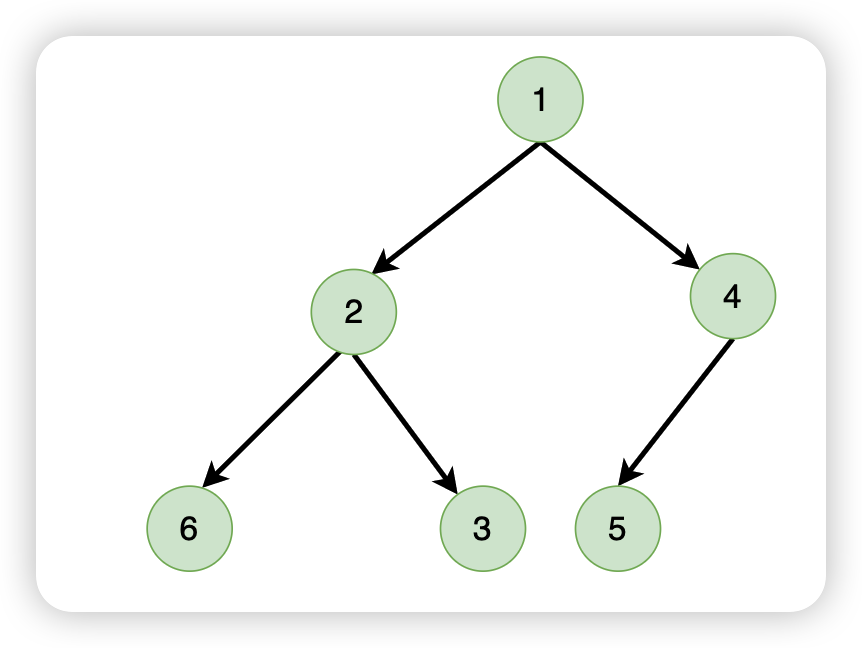
每一层的所有元素不一定比下一层（非自己的子节点）大或者小

二叉堆主要有两种类型：

最小堆：对于每个节点x，x的值小于等于它的左子节点和右子节点的值。
最大堆：对于每个节点x，x的值大于等于它的左子节点和右子节点的值。

堆的实现

二叉堆通常用数组来实现

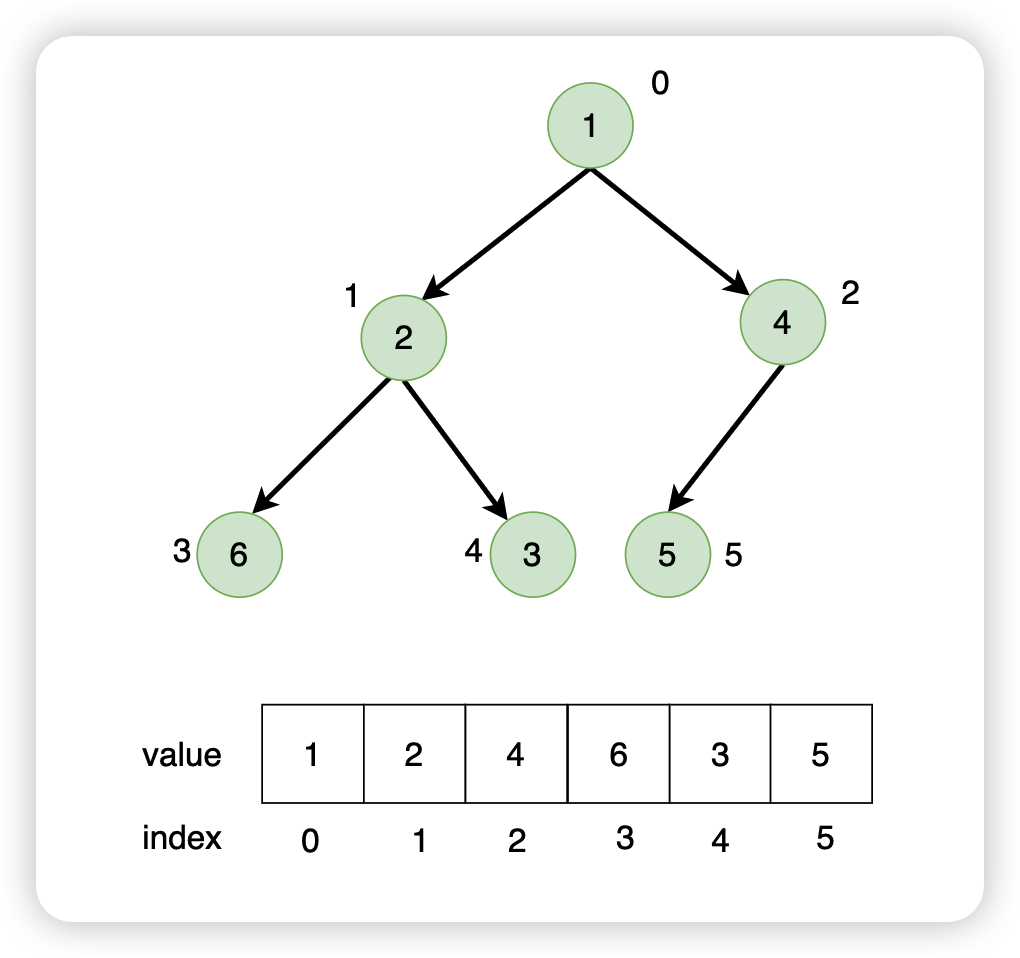
通过数组，我们可以非常方便的找到一个节点的所有亲属。对于任意节点i，它的左孩子的索引为2i+1，右孩子的索引为2i+2，父节点的索引为(i-1)/2。例如：

父节点：Math.floor((i - 1) / 2)

子节点索引	父节点索引
1	0
3	1
4	1
5	2

左分支节点：i * 2 + 1

父节点索引	左分支节点索引
0	1
1	3
2	5

右分支节点：i * 2 + 2

父节点索引	右分支节点索引
0	2
1	4
2	6

react 中对最小堆的应用

在 react 中，最小堆对应的源码在 SchedulerMinHeap.js 文件中，总共有 6 个方法，其中向外暴露了 3 个方法

push：向最小堆推入一个元素
pop：弹出一个
peek：取出第一个

没有暴露的是：

siftUp：向上调整
siftDown：向下调整
compare：这是一个辅助方法，就是两个元素做比较的

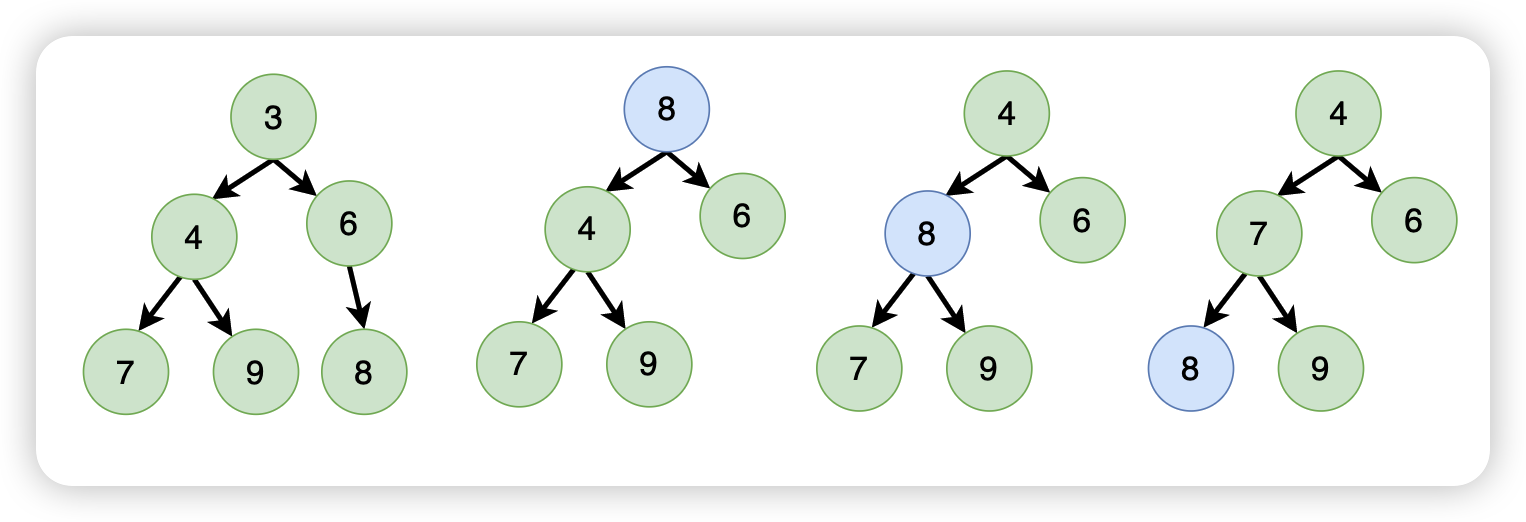
所谓向上调整，就是指将一个元素和它的父节点做比较，如果比父节点小，那么就应该和父节点做交换，交换完了之后继续和上一层的父节点做比较，依此类推，直到该元素放置到了正确的位置

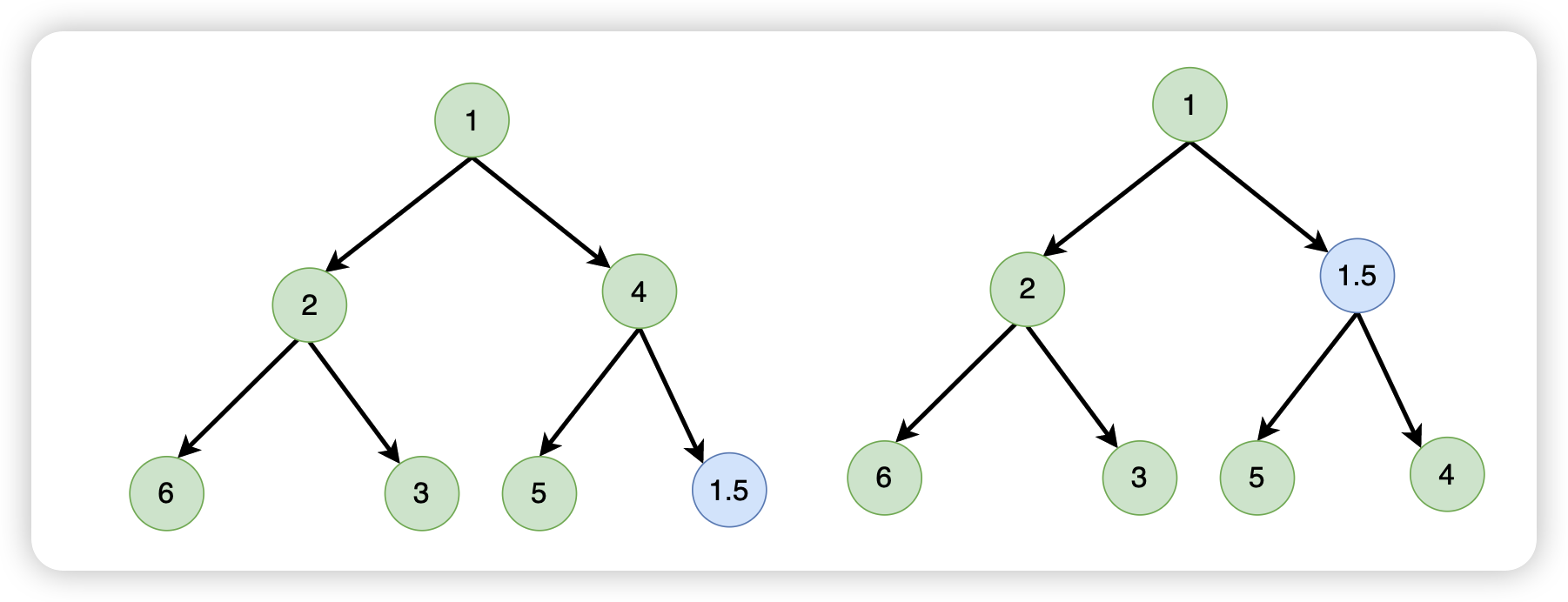
向下调整，就刚好相反，元素往下走，先和左分支进行比较，如果比左分支小，那就交换。

接下来我们学习 React 最小堆算法源码的具体实现

peek

取出堆顶的任务，堆顶一定是最小的

这个方法极其的简单，如下：

peek(timerQueue);
export function peek(heap) {
  // 返回这个数组的第一个元素
  return heap.length === 0 ? null : heap[0];
}

push

向最小堆推入一个新任务，因为使用的是数组，所以在推入任务的时候，首先该任务是被推入到数组的最后一项，但是这个时候，涉及到一个调整，我们需要向上调整，把这个任务调整到合适的位置

push(timerQueue, newTask);
export function push(heap, node) {
  const index = heap.length;
  // 推入到数组的最后一位
  heap.push(node);
  // 向上调整，调整到合适的位置
  siftUp(heap, node, index);
}

pop

pop 是从任务堆里面弹出第一个任务，也就是意味着该任务已经没有在队列里面了

pop(taskQueue);
export function pop(heap) {
  if (heap.length === 0) {
    return null;
  }
  // 获取数组的第一个任务（一定是最小的）
  const first = heap[0];
  // 拿到数组的最后一个
  const last = heap.pop();
  if (last !== first) {
    // 将最后一个任务放到第一个
    heap[0] = last;
    // 接下来向下调整
    siftDown(heap, last, 0);
  }
  return first;
}