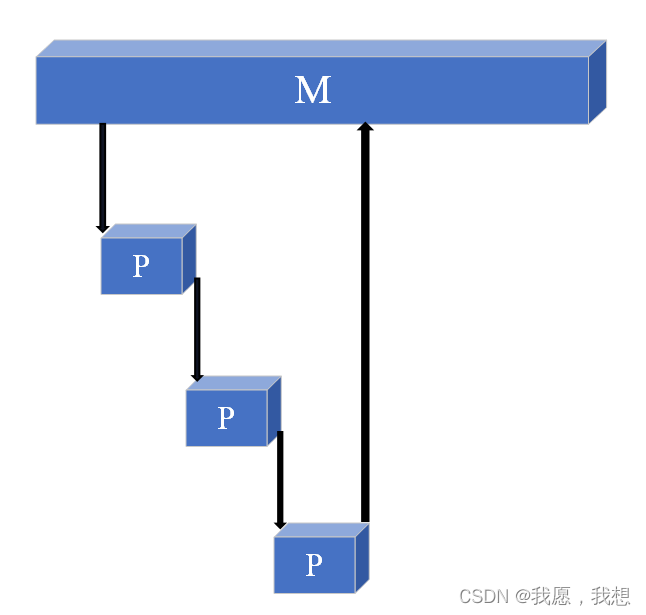
Numpy的轴

import numpy as np
数组=np.array([[[1,2],[4,5],[7,8]],[[8,9],[11,12],[14,15]],[[10,11],[13,14],[16,17]],[[19,20],[22,23],[25,26]]])
print(数组.shape) # 返回 (4, 3, 2)
最内层一对 [ ] 可以代表一个1维数组
加粗的一对 [ ] 里面有3个一维数组,也就是2维数组
最外层的一对 [ ] 里面有3个2维数组也就是3维数组
0轴是行,1轴是列,2轴是纵深
数组的shape维度是(4,3,2),元组的索引为 [ 0,1,2 ]
假设维度是(2,3),元组的索引为[0,1]
假设维度是(4,) 元组的索引为[0]
可以看到轴编号和shape元组的索引是对等的,所以这个编号可以理解为高维nd.array.shape产生的元组的索引
我们知道shape(4,3,2)表示数组的维度,既然shape的索引可以看做轴编号,那么一条轴其实就是一个维度
0轴对应的是最高维度3维,1轴对应2维,2轴对应的就是最低维度的1维
总结:凡是提到轴,先看数组的维度,有几维就有几个轴
沿轴切片
import numpy as np
数组=np.array([ [1,2,3] , [4,5,6] , [7,8,9] ])
print(数组)
print(数组.shape)
数组的维度是(3,3),这个元组的索引是 [0,1],表示这个2维数组有两条轴:0轴和1轴
首先看1个参数的切片操作:
print(数组[0:2])
这里有个很重要的概念, :2 是切片的第一个参数,约定俗成第一个参数就代表0轴
0轴表示2维,所以这个切片是在2维这个维度上切的,又叫“沿0轴切”。

这个2维数据是由3个1维数组组成的,这3个1维数组当然也有索引号也是[0,1,2],[ :2 ] 就表示它要切取2维(0轴)上3个1维数组中的索引 [ 0 ] 和索引 [ 1 ] ,于是得到 ([ 1, 2, 3 ]) 和 ([ 4, 5, 6 ]) 这两个1维数组。
首先看2个参数的切片操作:
print(数组[:2,1:])
就是在两个维度(轴)上各切一刀,第1个参数就是2维(0轴), :2 表示切取2维(0轴)上的索引 [ 0 ] 和索引 [ 1 ] ,即 ([ 1, 2, 3 ]) 和 ([ 4, 5, 6 ]) 这两个1维数组
第2个参数就是1维(1轴),1: 表示切取1维(1轴)上的索引 [ 1 ] 和索引 [ 2 ] ,即对数组 ([ 1, 2, 3 ]) 取 ([ 2,3 ]) ,对数组 ([ 4, 5, 6 ]) 取 ([ 5,6 ])

传入轴编号怎么理解
import numpy as np
数组=np.arange(16).reshape((2, 2, 4))
print(数组)
print(数组.shape)
数组的维度:(2,2,4) 元组索引(下标):[0,1,2]
我们转换它:
3维数组的1维(2轴)上是4个一维数组,每个1维数组都有一个由0,1两个轴编号组成的索引 [ 0,0 ] , [ 0,1 ] , [ 1,0 ] , [ 1,1 ],transpose方法传入的参数是轴编号 (1, 0, 2) 在就是把元组的索引顺序改变成 [ 1,0,2 ] 也就是把数组 [ 0,1 ] 的一维数组变成数组[ 1,0 ]

numpy数组转置换轴


transpose方法 【行列转置】
import numpy as np
数组=np.arange(24).reshape((4,6))
print(数组)
print("-"*30)
print(数组.transpose())

swapaxes方法 【轴转置】
mport numpy as np
数组=np.arange(24).reshape((4,6))
print(数组)
print("-"*30)
print(数组.swapaxes(1,0))