第五天 周日 休息~【提醒补坑:链表总结还没写】
一、参考资料
哈希表理论基础
文章连接:https://programmercarl.com/%E5%93%88%E5%B8%8C%E8%A1%A8%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
有效的字母异位词
题目链接/文章讲解/视频讲解:https://programmercarl.com/0242.%E6%9C%89%E6%95%88%E7%9A%84%E5%AD%97%E6%AF%8D%E5%BC%82%E4%BD%8D%E8%AF%8D.html
快乐数
题目链接/文章讲解:https://programmercarl.com/0202.%E5%BF%AB%E4%B9%90%E6%95%B0.html
两数之和
题目链接/文章讲解/视频讲解:https://programmercarl.com/0001.%E4%B8%A4%E6%95%B0%E4%B9%8B%E5%92%8C.html
二、哈希表理论基础
场景需要:当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
1.哈希表的定义
哈希表(Hash table),也称为散列表。是根据关键码的值而直接进行访问的数据结构。更为直白而言,数组就是一张哈希表。
2.解决的问题
一般用于快速判断一个元素是否在集合中。时间复杂度为O(1)。
3.基本概念理解:
1)哈希函数(哈希碰撞、拉链法、线性探测/开放寻址法)
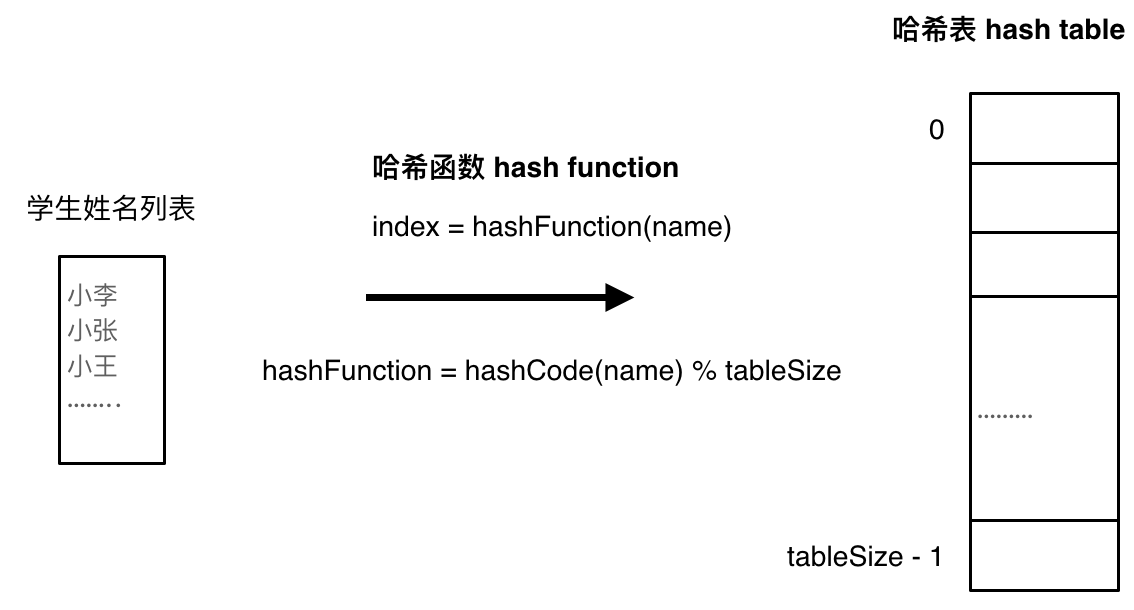
图片来源: https://programmercarl.com/%E5%93%88%E5%B8%8C%E8%A1%A8%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E5%93%88%E5%B8%8C%E8%A1%A8
哈希函数(hash function)指将哈希表中元素的关键键值映射为元素存储位置的函数。
2)哈希碰撞
如果不同的输入经哈希映射得到了同一个哈希值,就发生了"哈希碰撞"(collision)。
常用的两种解决办法:拉链法、线性探测/开放寻址法
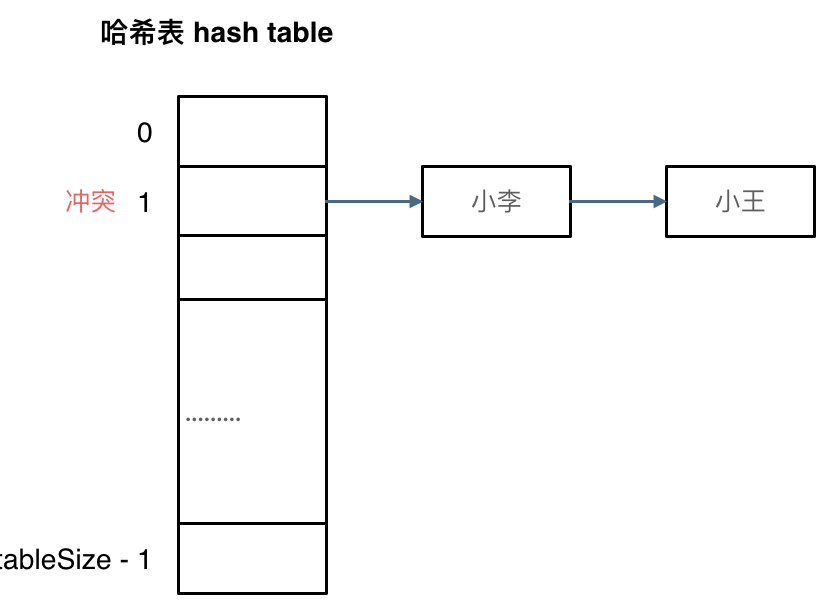
① 拉链法
拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
图示:小李和小王在索引1的位置发生了冲突,发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王。(数据规模是dataSize, 哈希表的大小为tableSize)

② 线性探测/开放寻址法
使用线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。
例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。图示:

3)常见的三种哈希结构
数组
集合set
映射map
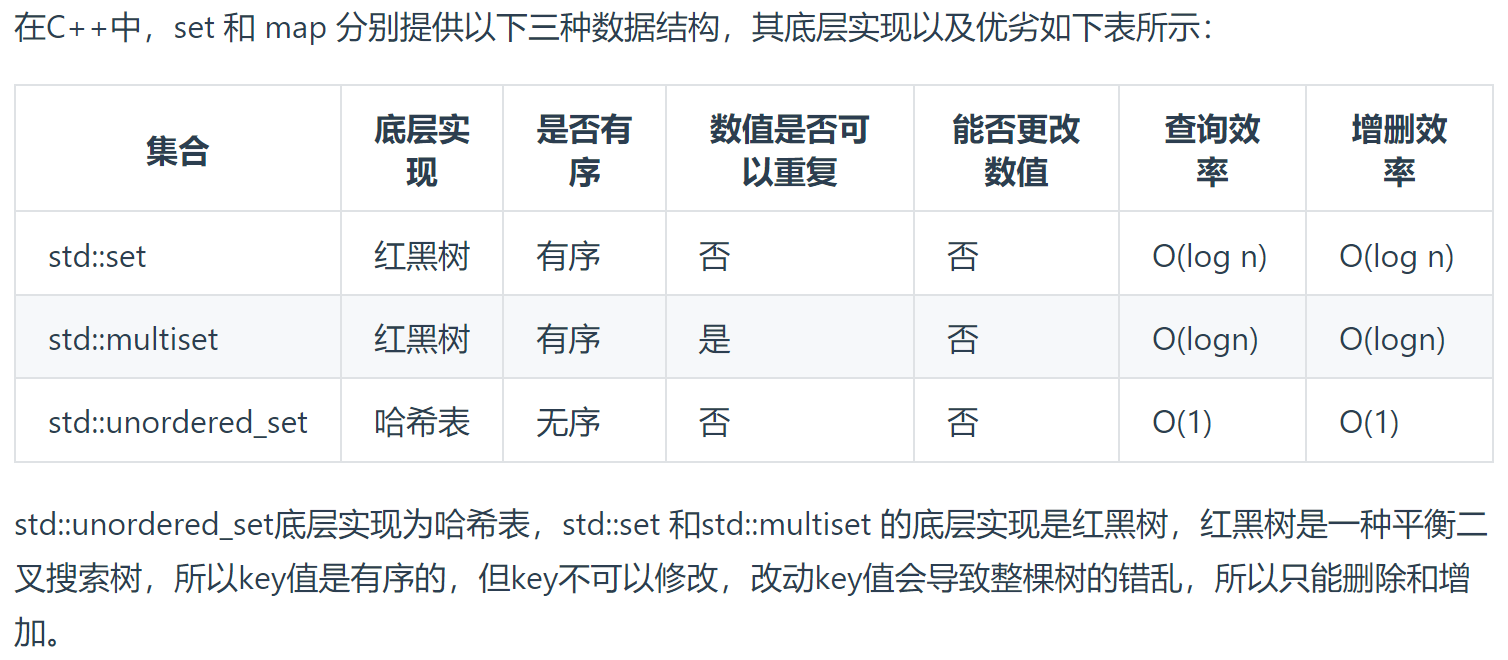
图片来源: https://programmercarl.com/%E5%93%88%E5%B8%8C%E8%A1%A8%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E5%B8%B8%E8%A7%81%E7%9A%84%E4%B8%89%E7%A7%8D%E5%93%88%E5%B8%8C%E7%BB%93%E6%9E%84
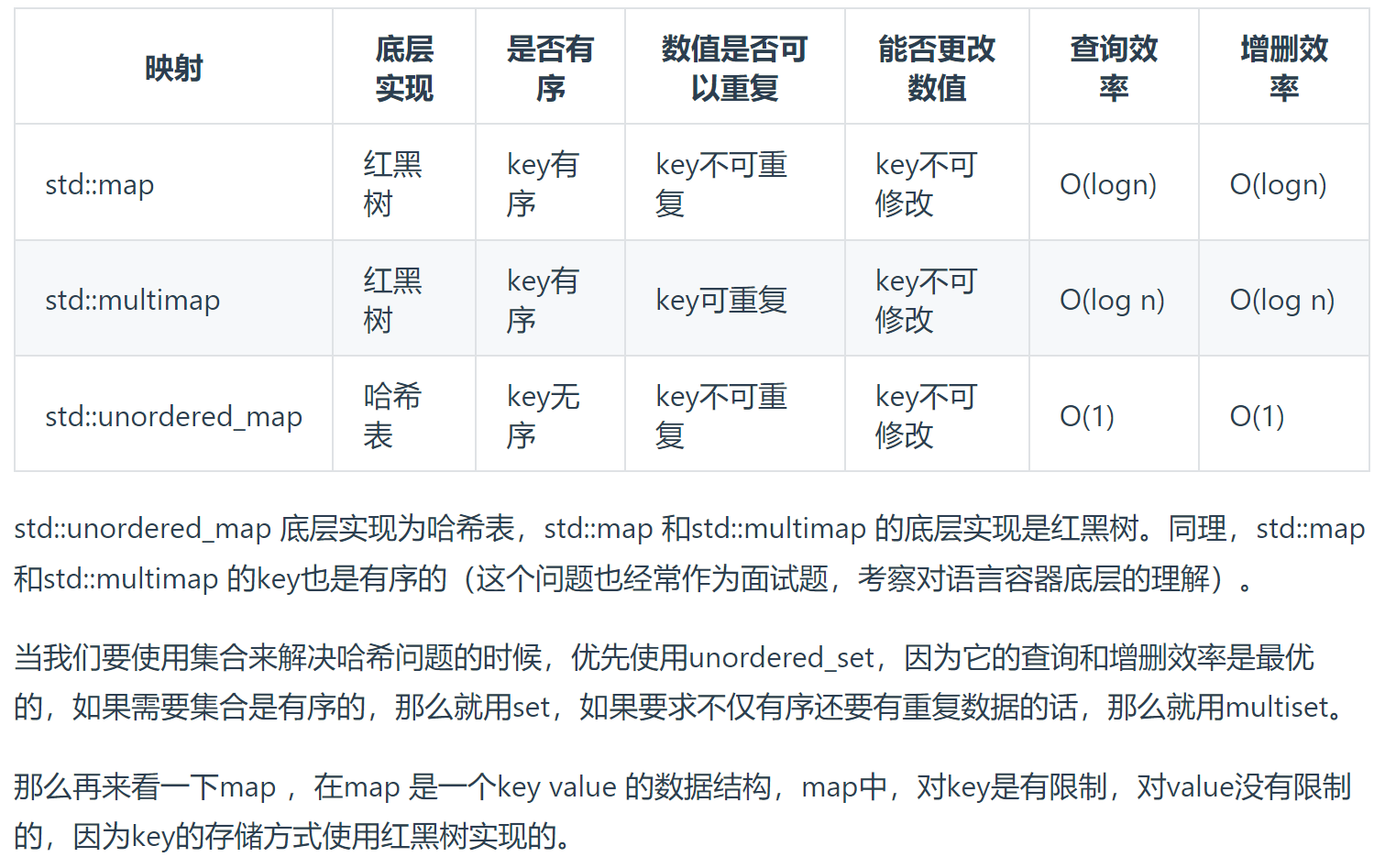
4)参考链接
https://blog.csdn.net/weixin_44129618/article/details/122499313
https://cloud.tencent.com/developer/article/1776352
三、LeetCode242-有效的字母异位词
class Solution {
public:
bool isAnagram(string s, string t) {
// 将字符映射到数组中,大小为26,初始化均为0
int record[26] = {0};
// 题目中假设字符串只有小写字母,,ASCII码记为s[i] - 'a' 即可
for (int i = 0; i < s.size(); i++) {
record[s[i] - 'a']++;
}
for (int i = 0; i < t.size(); i++) {
record[t[i] - 'a']--;
// 提前判断一部分情况
if (record[t[i] - 'a'] < 0) {
return false;
break;
}
}
for (int i = 0; i < 26; i++) {
if (record[i] > 0) {
return false;
}
}
return true;
}
};四、LeetCode349-两个数组的交集
class Solution {
public:
// 用unordered_set——无序、速度快
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
// 定义结果集,用set可以实现去重
unordered_set<int> result_set;
// 对nums1数组进行去重处理
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 判断交集——nums2的元素在nums_set中出现过
// 不明白为什么写成 nums_set.find(num) != nums_set.end()
// 原因是nums_set.find(num)返回一个迭代器,下面找到了unordered_map返回值的说明
// 返回值说明:如果给定的键存在于unordered_map中,则它向该元素返回一个迭代器,否则返回映射迭代器的末尾。
if (nums_set.find(num) != nums_set.end()) {
result_set.insert(num);
}
}
// 最终的结果
vector<int> result_v(result_set.begin(), result_set.end());
return result_v;
}
};五、LeetCode202-快乐数
class Solution {
public:
// 殊不知,这题转化成用哈希法解决,巧妙的化解“无限循环”的问题
// 快乐数是一道穿着糖衣的哈希经典题——判断某元素是否在集合里出现过
//「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
// 取数值各个位上的元素之和
int getSum(int n) {
int sum = 0;
while (n) {
sum += (n % 10) * (n % 10);
n = n / 10;
}
return sum;
}
// 判断是否为【快乐数】
bool isHappy(int n) {
unordered_set<int> set;
while(true) {
int sum = getSum(n);
if (sum == 1) {
return true;
}
// 如果这个值在集合中出现过,返回false
if (set.find(sum) != set.end()) {
return false;
} else {
set.insert(sum);
}
n = sum;
}
}
};六、LeetCode1-两数之和
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> map;
for (int i = 0 ; i < nums.size(); i++) {
// 遍历当前元素,并在map中寻找是否有匹配的key
auto iter = map.find(target - nums[i]);
if (iter != map.end()) {
// 这个值出现过,说明iter对应的元素下标较小
return {iter->second, i};
}
// 如果没找到匹配对,就将该元素加入map中
map.insert(pair<int, int>(nums[i], i));
}
return {};
}
};
总结:
代码注释的一些感悟和理解,希望能常看常感悟;
C++的语法使用又熟练了一大步;
快乐数的糖衣迷惑值得记住,学会变通的逻辑思维方式;
两数之和巧妙运用了unordered_map映射,快速又精准的解决了问题。
【记得有空填坑】
刷题加油鸭~~


![[标准库]STM32F103R8T6 标准库配置RCC时钟和超频](https://img-blog.csdnimg.cn/648eebe7441745338f489474861d3386.png)