Day 46 139.单词拆分

news2024/9/25 19:22:30

单词拆分

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。

你可以假设字典中没有重复的单词。

示例 1：

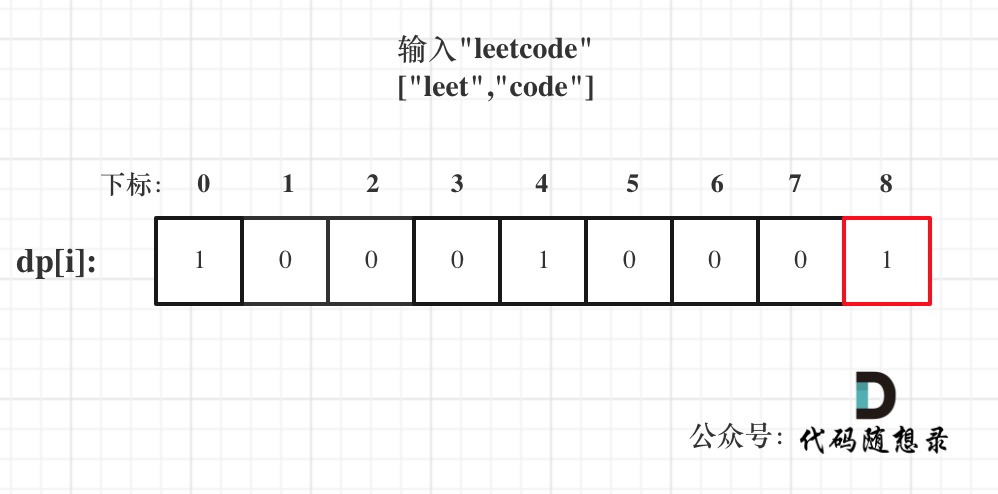
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。

示例 2：

输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。
注意你可以重复使用字典中的单词。

示例 3：

输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

单词视为物品，字符串视为背包，又因为可以重复使用，所以是完全背包；

动规五部曲：

1.确定dp数组以及下标的含义

dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2.确定递推公式

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

3.dp数组如何初始化

从递推公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]一定是true，否则递推下去后面都都是false了；

那么dp[0]有没有意义呢？dp[0]表示如果字符串为空的话，能否在字典中找到，很明显应该是false;

但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况，那么dp[0]怎样定义其实无所谓了；

下标非0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词；

其实很多时候都会出现这种dp[0]赋值和意义不一致的情况，以递推公式为主；

4.确定遍历顺序

讨论两层for循环的前后顺序。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

而本题其实求的是排列数，拿 s = “applepenapple”, wordDict = [“apple”, “pen”] 举例；

“apple”, “pen” 是物品，那么我们要求物品的组合一定是 “apple” + “pen” + “apple” 才能组成 “applepenapple”；

“apple” + “apple” + “pen” 或者 “pen” + “apple” + “apple” 是不可以的，此处就是强调物品之间顺序；

所以一定是先遍历背包，再遍历物品；

	for(int i = 1; i < s.size(); i++) {
		for(int j = 0; j < i; j++){
            string tempWord = s.substr(j, i - 1);
            if(dict.find(tempWord) != dict.end() && dp[j] == true){
                dp[i] = true;
            }
        }
	}

5.打印dp数组：

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
		unordered_set<string> wordSet(wordDict.begin(), wordDict.end());//转化为unordered_set（即wordSet）的原因是为了提高查找效率
        vector<bool> dp(s.size() + 1, 0);
        dp[0] = true;
        for(int i = 1; i <= s.size(); i++) {
			for(int j = 0; j < i; j++){
            	string tempWord = s.substr(j, i - j);
            	if(wordSet.find(tempWord) != wordSet.end() && dp[j] == true){
                	dp[i] = true;
            	}
        	}
		}
        return dp[s.size()];
    }
};

时间复杂度：O(n^3)，因为substr返回子串的副本是O(n)的复杂度（这里的n是substring的长度）

空间复杂度：O(n)

多重背包

多重背包本质上可以视为01背包，因为数量仍然是有限个；

每件物品最多有M件可用，把M件摊开，其实01背包问题了；

但是不能完全按照01背包的代码来写，因为vector扩容是一件非常耗时的事情；

递推公式写成如下的形式，把每种商品遍历的个数放在01背包里面在遍历一遍，再递推，就解决了：

$d p [j] = ma x (d p [j], d p [j - k * w e i g h t [i]] + k * v a l u e [i])$ ；

#include<iostream>
#include<vector>
using namespace std;
int main() {
    int bagWeight,n;
    cin >> bagWeight >> n;
    vector<int> weight(n, 0);
    vector<int> value(n, 0);
    vector<int> nums(n, 0);
    for (int i = 0; i < n; i++) cin >> weight[i];
    for (int i = 0; i < n; i++) cin >> value[i];
    for (int i = 0; i < n; i++) cin >> nums[i];

    vector<int> dp(bagWeight + 1, 0);

    for(int i = 0; i < n; i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
        }
    }

    cout << dp[bagWeight] << endl;
}