---

前言

前面一章我们学习到了程序逻辑语句，在写代码的过程中，我们会遇到需要重复使用的代码块，为此我们可以使用一个方法，把特定的代码块，包装起来，然后通过方法名进行调用。下面我们介绍方法。

---

1.方法的概念和使用

方法就是一个代码片段. 类似于 C 语言中的 “函数”。方法存在的意义(不要背, 重在体会):

1. 是能够模块化的组织代码(当代码规模比较复杂的时候).
2. 做到代码被重复使用, 一份代码可以在多个位置使用.
3. 让代码更好理解更简单.
4. 直接调用现有方法开发, 不必重复造轮子.
   比如：现在要开发一款日历，在日历中经常要判断一个年份是否为闰年，则有如下代码：

---

 //判断是否是闰年
    public static boolean isLeapYear(int y){
        if(y%400==0||(y%4==0&&y%100!=0)){
            return true;
        }else {
            return false;
        }
    }

2.方法的定义

语法格式:

//方法定义
修饰符 返回值类型 方法名称([参数类型 形参 …]){
方法体代码;
[return 返回值];
}

示例1：判断一个数是否是素数

public static void isPrimeNum(int n){
        int i = 2;
        for (; i <=Math.sqrt(n); i++) {
            if(n%i==0){
                break;
            }
        }
        if (i > Math.sqrt(n)) {
            System.out.println(n+"是素数");
        }else{
            System.out.println(n+"不是素数");
        }
    }

示例2：两数相加

public static int Add(int x,int y){
        return x+y;
    }

---

3.实参和形参的关系

咱们写一个交换两个整数的方法

    public static void Swap(int x,int y){
        int tmp=x;
        x=y;
        y=tmp;
    }

    public static void main(String[] args) {
        int x=10;
        int y=20;
        System.out.printf("交换前的x:%d,y:%d\n",x,y);
        Swap(x,y);
        System.out.printf("交换后的x:%d,y:%d\n",x,y);
    }

发现这样写，没有交换两个变量，
实参a和b是main方法中的两个变量，其空间在main方法的栈(一块特殊的内存空间)中，而形参x和y是swap方法中的两个变量，x和y的空间在swap方法运行时的栈中，因此：实参a和b 与 形参x和y是两个没有任何关联性的变量，在swap方法调用时，只是将实参a和b中的值拷贝了一份传递给了形参x和y，因此对形参x和y操作不会对实参a和b产生任何影响。
注意：对于基础类型来说, 形参相当于实参的拷贝. 即 传值调用。

---

4.方法重载

刚才我们创建两个整数的相加，然后再分别创建两个浮点数的相加，还有三个整数相加

 public static int AddInt(int x,int y){
        return x+y;
    }
    public static double AddDou(double x,double y){
        return x+y;
    }
    public static int AddTri(int x,int y,int z){
        return x+y+z;
    }
    public static void main(String[] args) {
        System.out.println(AddInt(10, 20));
        System.out.println(AddDou(10.2, 14.3));
        System.out.println(AddTri(10, 20, 30));
    }

我们会发现这样写比较冗余，可不可以用一个Add方法名，来把上面的所有的方法都可以进行调用。
答案是可以的，下面便是方法的重载

4.1.改进

    public static int Add(int x,int y){
        return x+y;
    }
    public static double Add(double x,double y){
        return x+y;
    }
    public static int Add(int x,int y,int z){
        return x+y+z;
    }

4.2.注意事项

注意：

1. 方法名必须相同
2. 参数列表必须不同(参数的个数不同、参数的类型不同、类型的次序必须不同)
3. 与返回值类型是否相同无关

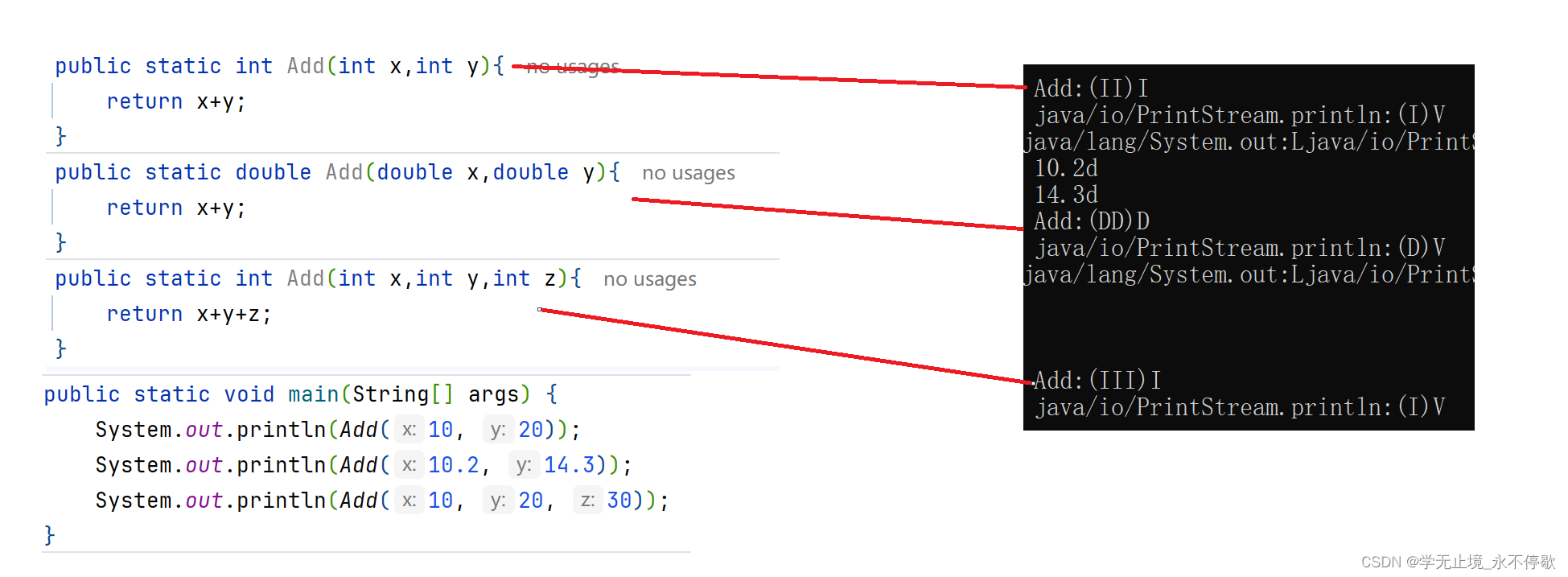
为什么会这样呢？
下来我们使用jdk的反汇编工具查看。将
上述代码经过编译之后，然后使用JDK自带的javap反汇编工具查看，具体操作：
4. 先对工程进行编译生成.class字节码文件
5. 在控制台中进入到要查看的.class所在的目录
6. 输入：javap -v 字节码文件名字即可

5.递归

5.1 生活中的故事

从前有坐山，山上有座庙，庙里有个老和尚给小和尚将故事，讲的就是：
"从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的就是：
“从前有座山，山上有座庙…”
“从前有座山……”
上面的故事有个共同的特征：自身中又包含了自己，该种思想在数学和编程中非常有用，因为有些时候，我们遇到的问题直接并不好解决，但是发现将原问题拆分成其子问题之后，子问题与原问题有相同的解法，等子问题解决之后，原问题就迎刃而解了

5.2 递归的概念

一个方法在执行过程中调用自身, 就称为 “递归”.
递归相当于数学上的 “数学归纳法”, 有一个起始条件, 然后有一个递推公式.
例如, 我们求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)!
递归的必要条件：

1. 将原问题划分成其子问题，注意：子问题必须要与原问题的解法相同
2. 递归出口
   代码示例: 递归求 N 的阶乘

 //阶乘
    public static int func(int x){
        if(x==1){
            return 1;
        }
        return x*func(x-1);
    }
    public static void main(String[] args) {
        int n=5;
        int ret=func(n);
        System.out.println(ret);
    }

5.3.练习

代码示例1 ：按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4)

public static void Print(int x){
        if(x>9){
            Print(x/10);
        }
        System.out.println(x%10);
    }
    public static void main(String[] args) {
        Print(1234);
    }

代码示例3 写一个递归方法，输入一个非负整数，返回组成它的数字之和. 例如，输入 1729, 则应该返回

 public static int sum(int x){
        if(x<=9){
            return x;
        }
        return x%10+sum(x/10);
    }

代码示例4 求斐波那契数列的第 N 项

public static int  Fib(int x){
        if(x==1||x==2){
            return 1;
        }
        return Fib(x-1)+Fib(x-2);
    }

---

完