2024/5/14：

        学编译原理的时候接触到了递归树的画法，中缀转后缀的解题过程和编译原理中的递归树有异曲同工之妙。今日解题的时候想了一下图解法，遂记录，本质上是对递归树的改进。

 图解原理概述

        以表达式 a+b*(c-d)+e 为例，先将其转化为二叉树，转化过程暂且不表，请读者自搜。总之能画成以下这样，若要得出后缀表达式则请后序遍历此树：

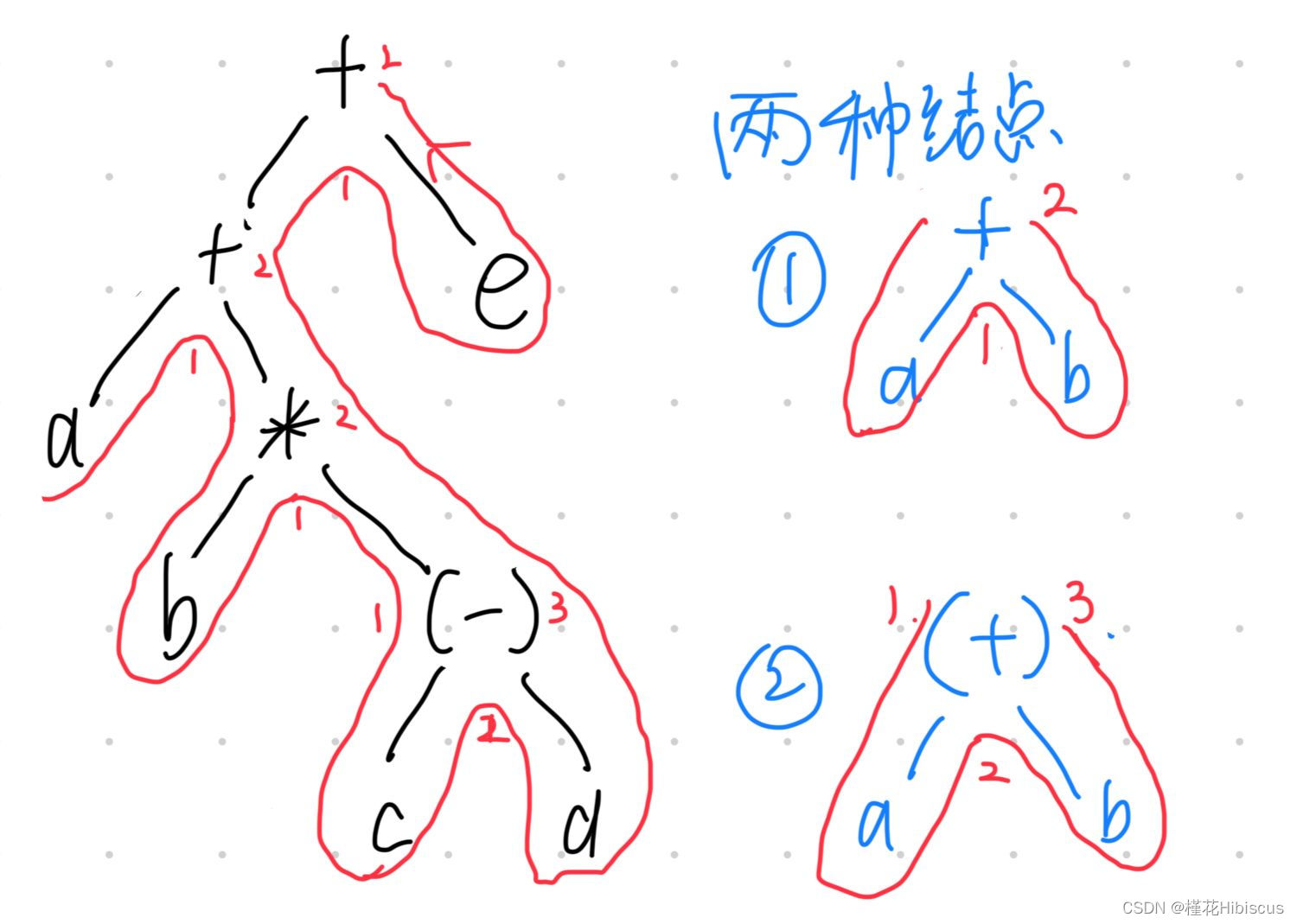
图1 基本结构图

        以上为构造的基本结构，跟普通的树不同的是里面增加了带括号的2型特殊节点。而红线即为递归的过程。

        对于1型节点来说，递归（红线）到1号位时，符号栈中增加该符号，而到2号位时出栈；而对于2型节点来说，递归（红线）到1号位时，符号栈中增加左括号，而到2号位时增加该符号，到3号位时弹出之前入栈的左括号和符号。各位仔细理解一下可以发现这和算法的处理方式是相同的。

---

例题

【2012年统考真题】已知操作符包括‘+’‘-’‘’‘/’‘（’‘）’ 。将中缀表达式a + b - a ( ( c + d ) / e - f ) + g转化为等价的后缀表达式a b + a c d + e / f - * - g + 时，用栈来存放暂时还不能确定运算次序的操作符。若栈初始时为空，则转换过程中同时保存在栈中的操作符的最大个数是（）

A. 5              B. 7              C. 8               D. 11

常规解法：见答案，可以看到正常写挺麻烦的。

图解法：

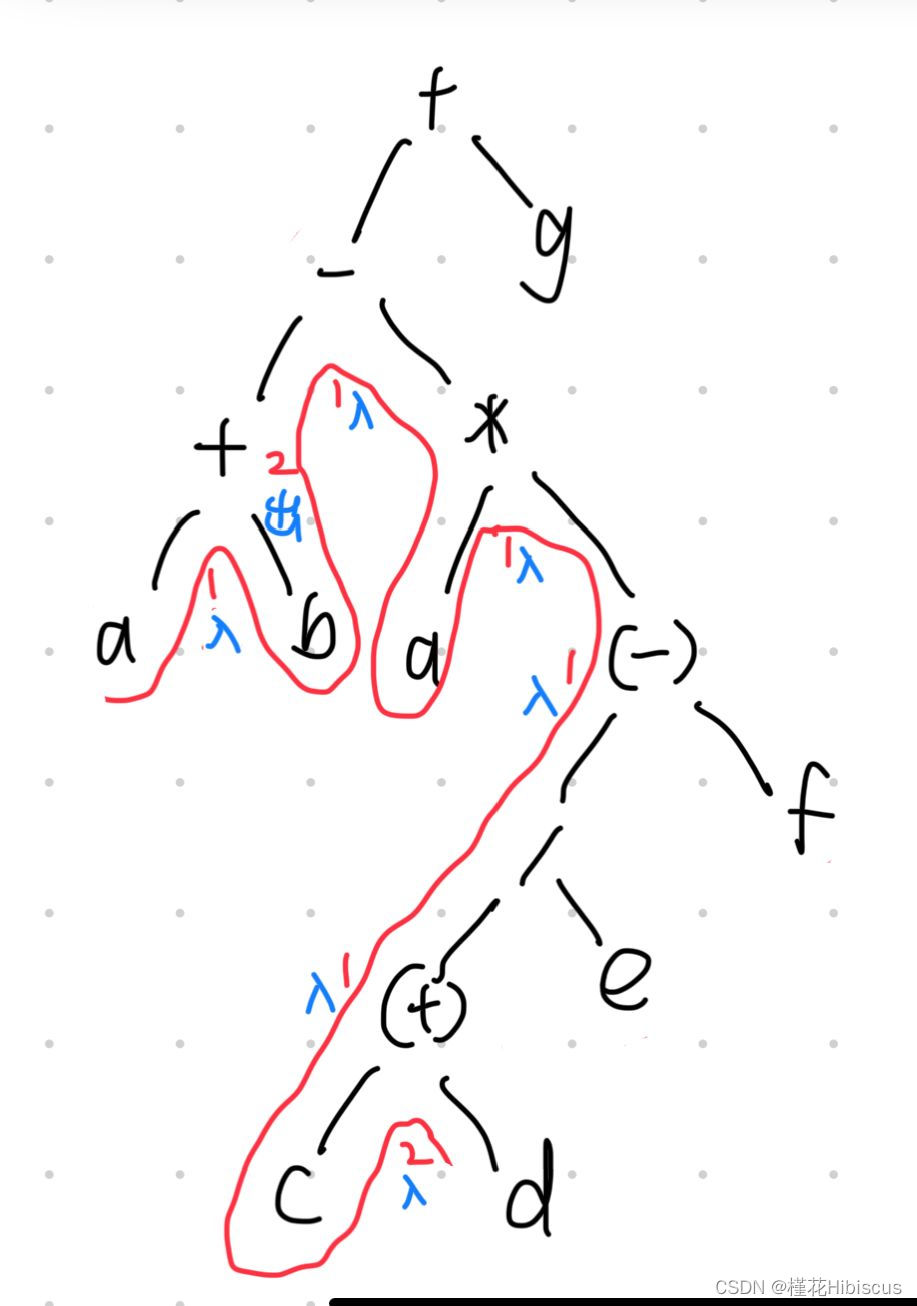
        图2 例题图解法答案

        简单画一画可以看到递归（红线）到最下面的2时同时保存在栈中的操作符最多，此时栈中元素为 - * ( ( + 一共五个，故选A。

【2015统考真题】假设栈初始为空，将中缀表达式a/b+(c*d-e*f)/g转化为等价的后缀表达式的过程中，当扫描到 f 时，栈中的元素依次是（）

A. +(*-              B. +(-*             C. /+(*-*             D. /+-*

        此题同样可用图解法作答，望读者自行思考（其实是我懒得写了）。

---

结尾

        希望对大家的学习有所启发。