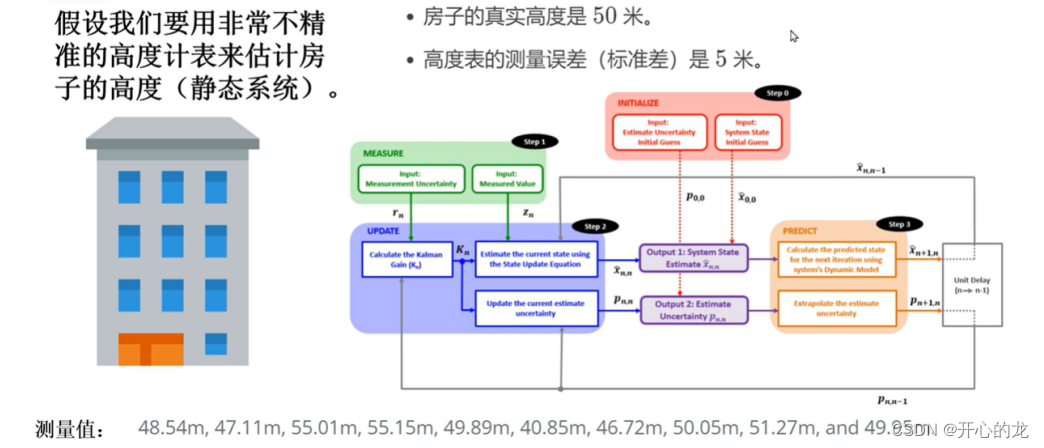
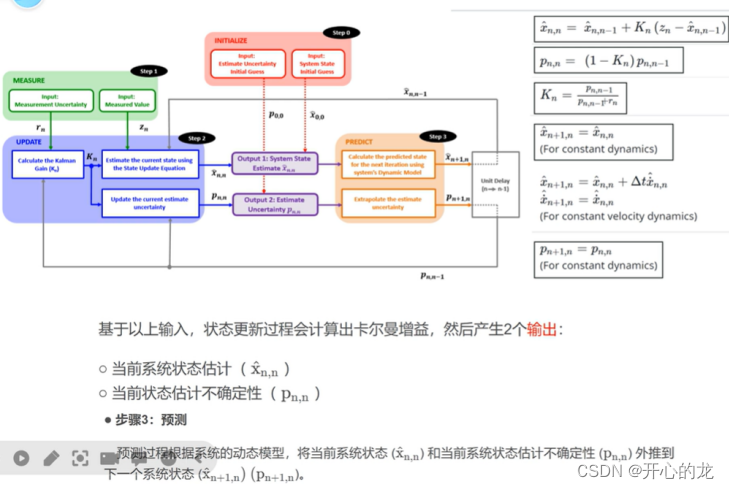
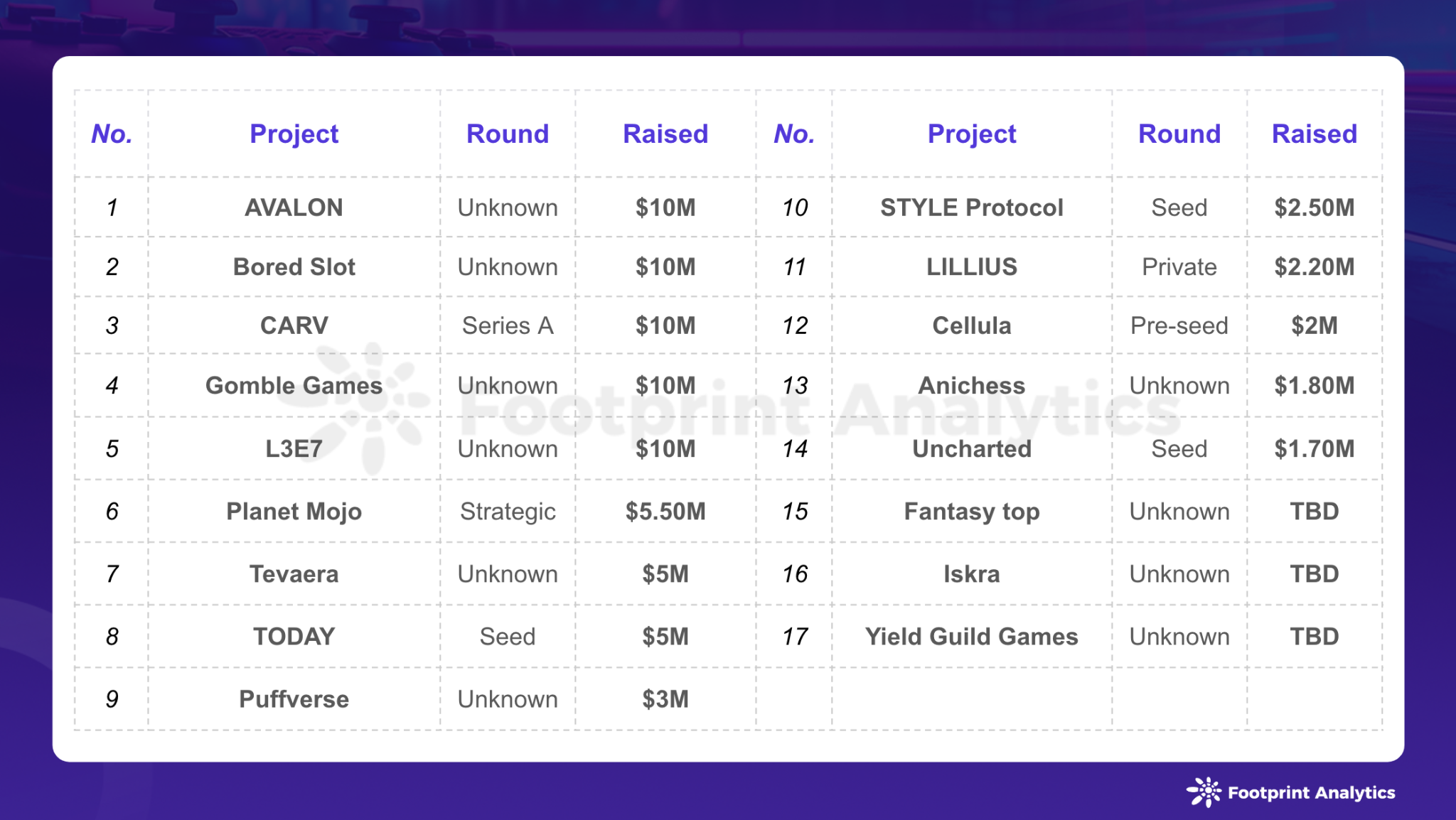
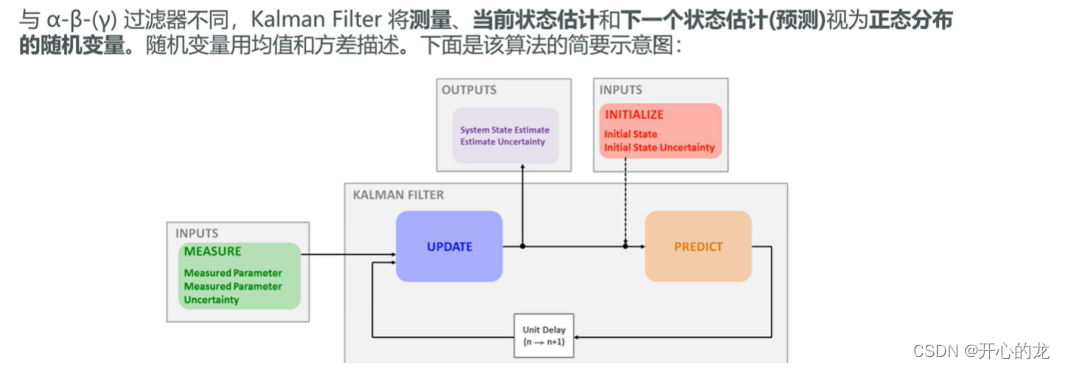
一维不带噪声的卡尔曼滤波方程有五个,下面分析剩余的三个方程:

 分析第一个例子,其中测量值和真实值之间的误差属于测量误差(使用准确性来描述),由于测量误差是随机的,我们可以使用方差来描述(表示距离均值的偏移程度),测量方程通常有传感器的供应商提供也可以通过校准得到,测量误差的方程实际上就是测量的不确定性,使用R来表示;
分析第一个例子,其中测量值和真实值之间的误差属于测量误差(使用准确性来描述),由于测量误差是随机的,我们可以使用方差来描述(表示距离均值的偏移程度),测量方程通常有传感器的供应商提供也可以通过校准得到,测量误差的方程实际上就是测量的不确定性,使用R来表示;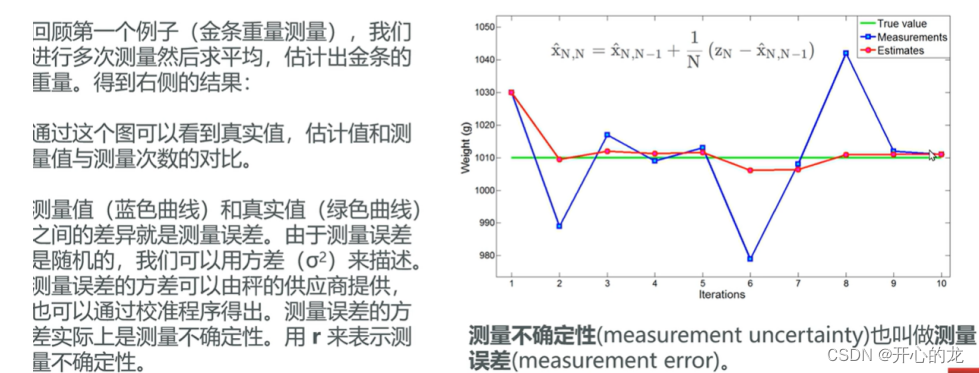
估计值与真实值之间的误差,我们称为估计误差,但是由于我们并不知道真实值,但是可以估计状态的不确定性,使用P来表示;
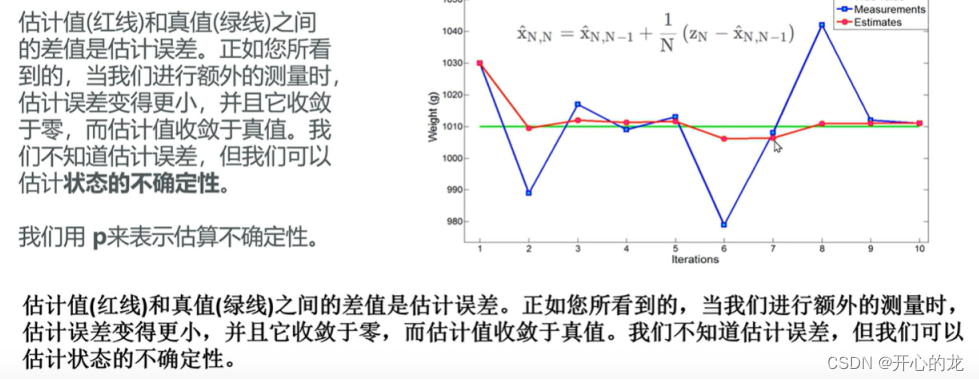
状态不确定性的描述
-
方差和协方差矩阵:
- 方差(对于一维状态)或协方差矩阵(对于多维状态)是描述状态不确定性的常用指标。
- 方差表示单一状态变量的不确定性程度,协方差矩阵则描述多个状态变量之间的相关性和不确定性。
-
概率分布:
- 假设状态变量服从某种概率分布(如高斯分布),可以用该分布的参数(均值和方差)来描述状态的不确定性。
- 高斯分布特别常用,因为其数学性质简洁且易于处;
测量不确定性R(测量误差) 就是测量值的方差






状态更新方程结合了俩个随机变量,分布是先验状态估计和测量值,卡尔曼滤波器是一种最优滤波器,它将两个随机变量结合起来,以最小化当前状态估计的不确定性;
当前状态估计是测量和先前状态估计的加权平均值;
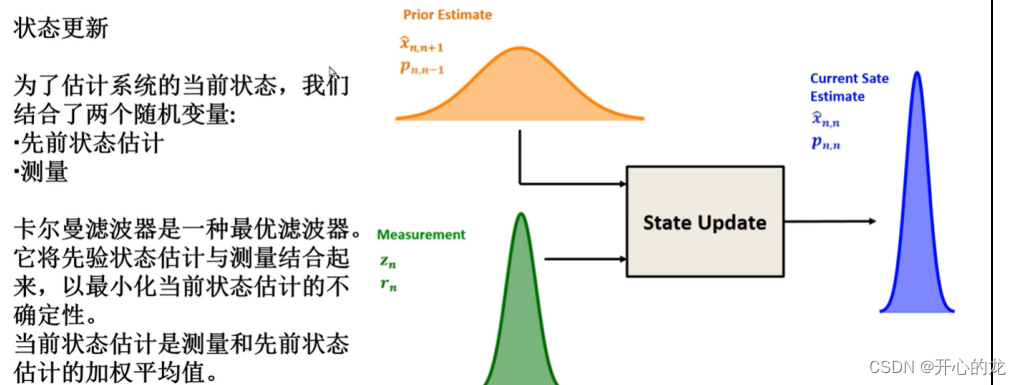 将状态更新方程化简得到,系统当前状态其实就是先验估计值和测量值的加权平均值;
将状态更新方程化简得到,系统当前状态其实就是先验估计值和测量值的加权平均值;
 要求出最优估计值,其实就是最小化最优估计值的方差,为了得到对应的W1,对其进行求偏导使偏导为0;
要求出最优估计值,其实就是最小化最优估计值的方差,为了得到对应的W1,对其进行求偏导使偏导为0;

化简得到了卡尔曼增益:
带入卡尔曼增益:


首先通过分析模型,状态外推方程,通过状态外推方程,推导出了协方差外推方程,令当前最优估计的方差最小,推导得到卡尔曼增益,再由卡尔曼增益球的协方差的更新方程;

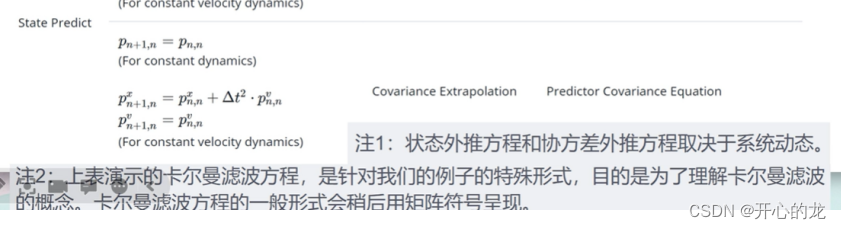
此时我们的流程图如下所示:
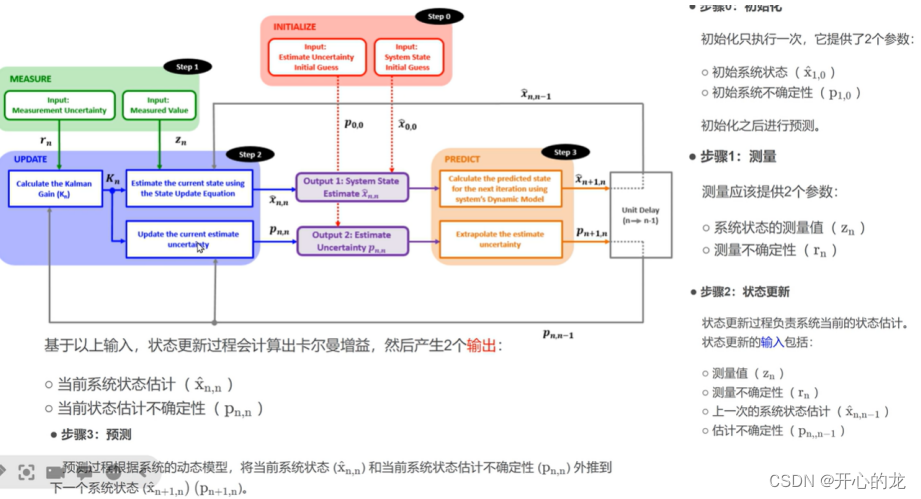
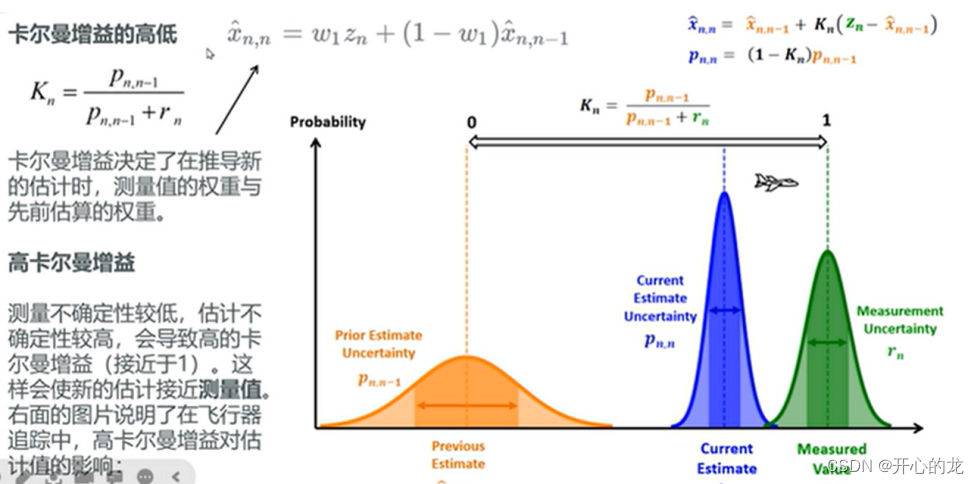
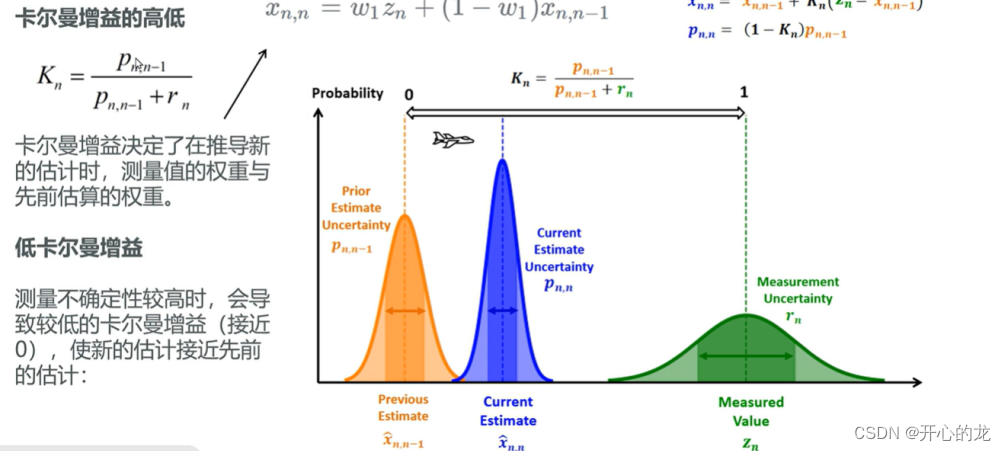
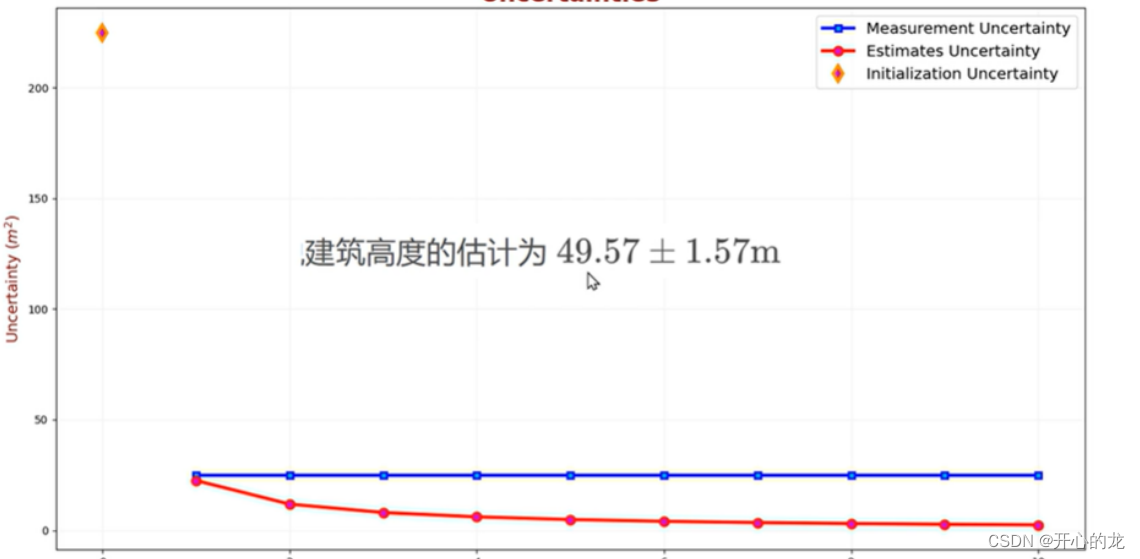
下面我们举例说明:
估计一个房子的高度: