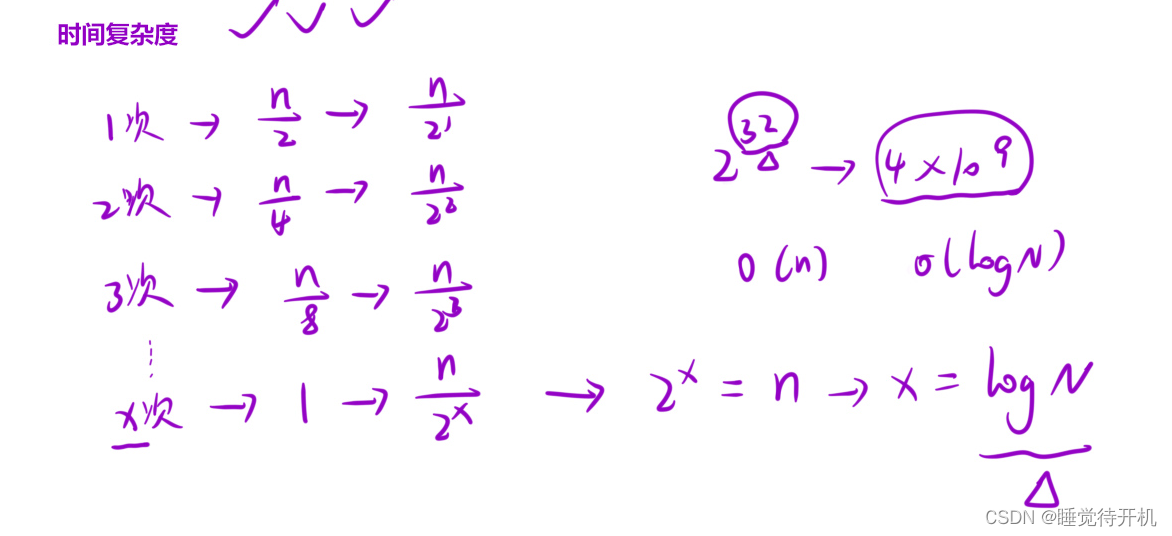#问题的引入-对于幂次方的求解我们怎么可以最大限度的降低时间复杂度呢
#对于一个基本的幂次运算,c++代码如下示例
long long int myPower(int base,int power)
{
long long int result = 1 ;
for (int i = 1 ; i <= power ; i++)
{
result *= base ;
}
return result ;
}#python代码示例
def myPower(base,power) :
res = 1
for i in range(power):
res *= base
return res##通过对一个问题的拆分-我们来了解快速幂到底是一个怎么样子的过程:
对于一个7**10,常规思想便是循环累乘,我们需要将10个7累乘起来,但是我们也可以将7**5,然后再平方也可以得到正确答案,我们也可以7*7,49*49*7,然后再平方我们也可以得到正确答案;显而易见,快速幂就是一个二分的思路,可以将原本的O(n)的时间复杂度降为O(logn)的时间复杂度。
##递归快速幂

当n为偶数的时候,计算a**(n//2),当n为奇数的时候,先计算a**((n-1)//2)再乘a。
##c++代码如下示例
int quickPower(int a,int n)
{
if (n == 0)
{
return 1 ; //递归的出口位置
}
else if (n % 2 == 1)
{
return quickPower(a,n-1) * a ;
}
else
{
int temp = quickPower(a,n/2);
return temp * temp ;
}
return 0 ;
//temp这个变量是必要的,quickPower(a,n/2) * quickPower(a,n/2),算法的时间复杂度会退化成O(n)
}##python代码如下示例
def quickPower(a,n):
if n == 0 :
return 1
elif n % 2 == 1 :
return quickPower(a,n-1) * a
else:
temp = quickPower(a,n/2)
return temp * temp##递归快速幂(对大素数取模)
##c++代码示例
#define MOD 1000000007
typedef long long ll ;
ll quickPower(ll a,ll n)
{
if (n == 0)
{
return 1 ;
}
else if (n % 2 == 1)
{
return quickPower(a,n/2) % MOD ;
}
else
{
ll temp = quickPower(a,n/2) % MOD
return temp * temp % MOD ;
}
}##非递归快速幂
#c++代码示例
int quickPower(int a,int n)
{
int ans = 1 ;
while (n):
if (n & 1)
{
ans *= a ;
}
a *= a ;
n >>= 1 ;
return ans ;
} 
##python代码示例
def quickPower(a,n):
res = 1
while n :
if n & 1 :
res *= a
a *= a
n >>= 1
return res在算 𝑎**n 时,只要a的数据类型支持乘法且满足结合律,快速幂的算法都是有效的。矩阵、高精度整数,都可以照搬这个思路。下面给出一个c++模板:
//非递归快速幂模板-泛型
template <typename T>
T quickPower(T a,T n)
{
T ans = 1 ;
while (n)
{
if (n & 1)
{
ans = ans * a ;
}
n >>= 1 ;
a = a * a ;
}
return ans ;
//最好别用自乘,重载完*还得重载*=
}##题目示例(洛谷1962-求解斐波那契数列-快速幂的经典应用):

##题目分析
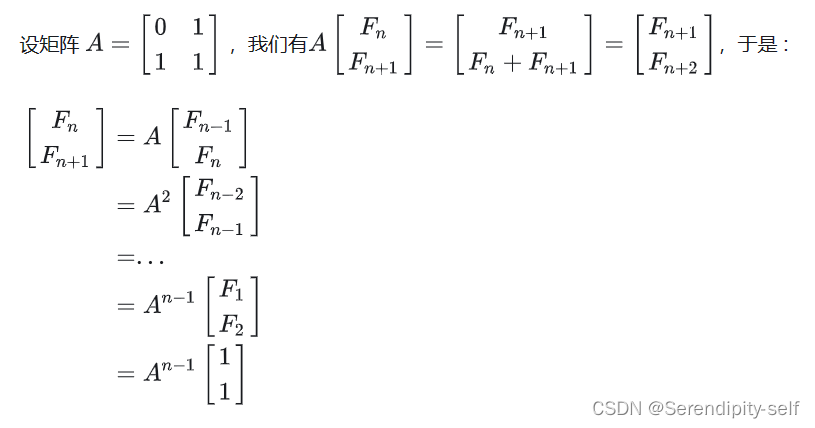
我们通过基本的线性代数知识可以进行推导出来如下图示
##c++代码示例
#include <cstdio>
#define MOD 1000000007
typedef long long ll ;
struct matrix
{
ll a1,a2,b1,b2 ;
//构造函数中初始化这四个成员变量。重载了乘法运算符,实现了两个矩阵相乘的功能。
matrix(ll a1 , ll a2 , ll b1 , ll b2) : a1(a1) , a2(a2) , b1(b1) , b2(b2) {}
matrix operator*(const matrix &y)
{
matrix ans(
(a1 * y.a1 + a2 * y.b1) % MOD,
(a1 * y.a2 + a2 * y.b2) % MOD,
(b1 * y.a1 + b2 * y.b1) % MOD,
(b1 * y.a2 + b2 * y.b2) % MOD
) ;
return ans ;
}
};
matrix quickPower(matrix a , ll n)
{
matrix ans(1,0,0,1) ; //单位矩阵
while (n)
{
if (n & 1)
{
ans = ans * a ;
}
a = a * a ;
n >>= 1 ;
}
return ans ;
}
int main()
{
ll x ;
matrix M(0,1,1,1) ;
scanf("%lld",&x);
matrix ans = quickPower(M,x-1) ;
printf("%lld\n",(ans.a1,ans.a2) % MOD) ;
return 0 ;
}#python代码示例
MOD = 1000000007
# import torch
class Matrix:
def __init__(self,a1,a2,b1,b2):
self.a1 = a1
self.a2 = a2
self.b1 = b1
self.b2 = b2
def __mul__(self, y):
return Matrix( (self.a1 * y.a1 + self.a2 * y.b1) % MOD,
(self.a1 * y.a2 + self.a2 * y.b2) % MOD,
(self.b1 * y.a1 + self.b2 * y.b1) % MOD,
(self.b1 * y.a2 + self.b2 * y.b2) % MOD)
def quick_power(n):
ans = Matrix(1,0,0,1)
a = Matrix(0,1,1,1)
while n :
if n & 1 :
ans = ans.__mul__(a)
a = a.__mul__(a)
n >>= 1
return ans
x = int(input())
# M = Matrix(0,1,1,1)
ans = quick_power(x-1)
print((ans.a1 * 1 + ans.a2 * 1) % MOD)