代码随想录算法训练营Day 42| 动态规划part04 | 01背包问题理论基础I、01背包问题理论基础II、416. 分割等和子集

---

---

01背包问题理论基础

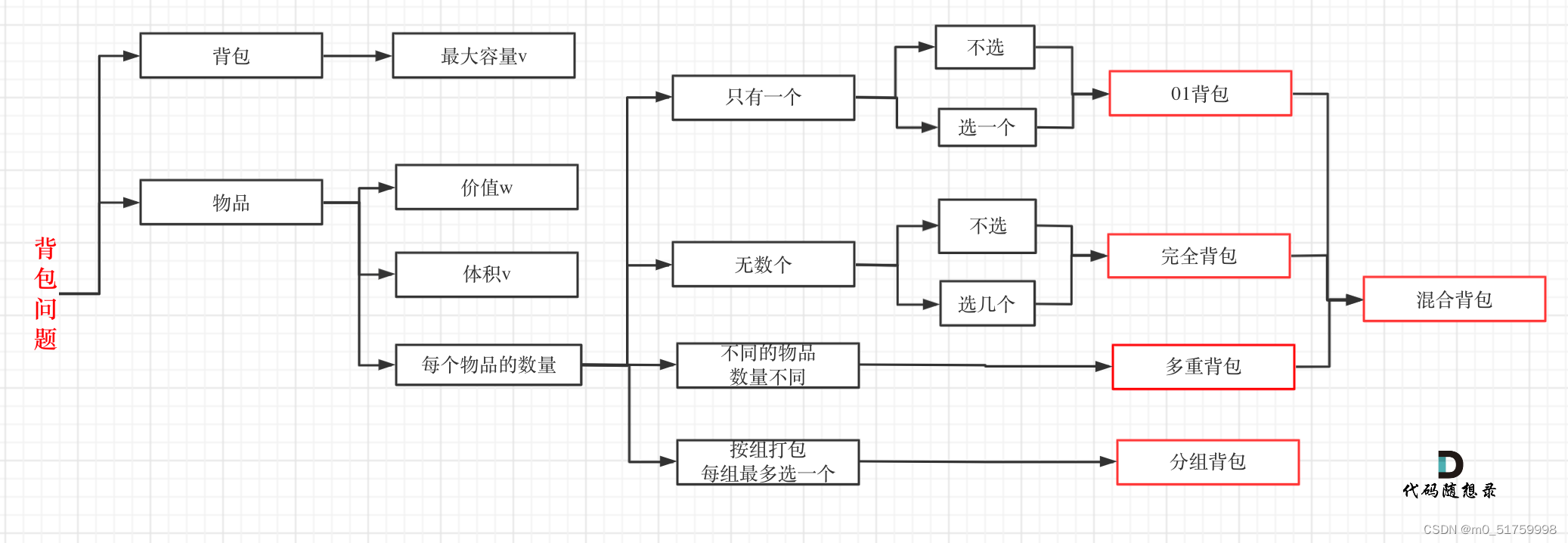
一、01背包问题

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。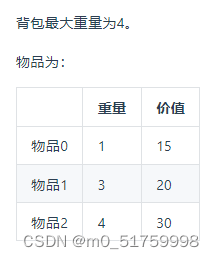

二、一维dp

def test_1_wei_bag_problem(weight, value, bagWeight):
    # 初始化
    dp = [0] * (bagWeight + 1)
    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    return dp[bagWeight]


if __name__ == "__main__":

    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4

    result = test_1_wei_bag_problem(weight, value, bagweight)
    print(result)

三、二维dp

def test_2_wei_bag_problem1(weight, value, bagweight):
    # 二维数组
    dp = [[0] * (bagweight + 1) for _ in range(len(weight))]

    # 初始化
    for j in range(weight[0], bagweight + 1):
        dp[0][j] = value[0]

    # weight数组的大小就是物品个数
    for i in range(1, len(weight)):  # 遍历物品
        for j in range(bagweight + 1):  # 遍历背包容量
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

    return dp[len(weight) - 1][bagweight]

if __name__ == "__main__":

    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4

    result = test_2_wei_bag_problem1(weight, value, bagweight)
    print(result)

---

416. 分割等和子集

题目链接

一、dp

class Solution(object):
    def canPartition(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """
        if sum(nums) % 2 != 0:
            return False
         # dp[i]中的i表示背包内总和
        # 题目中说：每个数组中的元素不会超过 100，数组的大小不会超过 200
        # 总和不会大于20000，背包最大只需要其中一半，所以10001大小就可以了2
        dp = [0]*10001 # 或者dp =[0]*(target+1)
        target = sum(nums)//2
        for i in range(1,len(nums)):
            for j in range(target,nums[i]-1,-1):
                dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])      
        return dp[target]==target