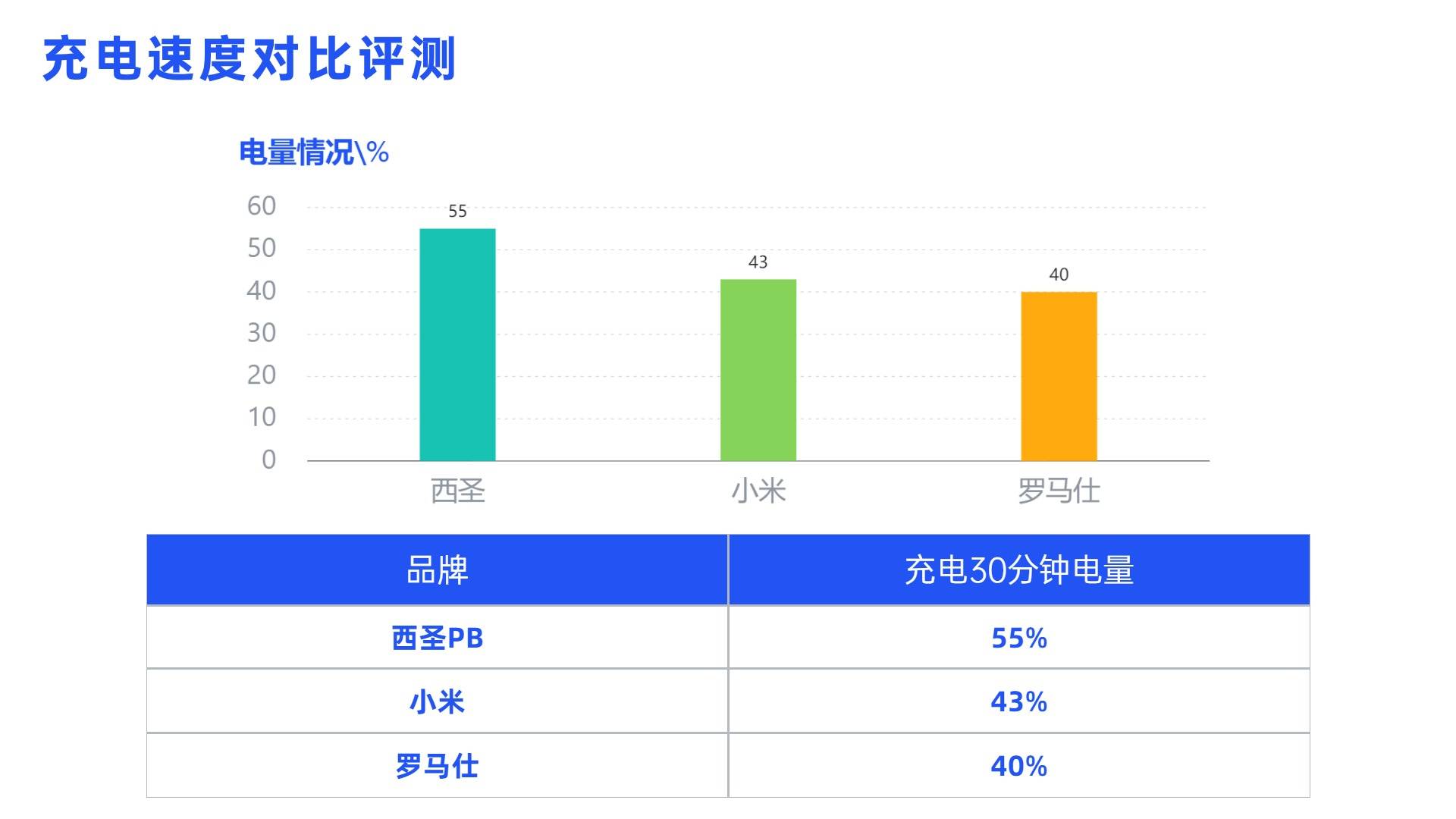
Python 机器学习 基础 之 监督学习 [朴素贝叶斯分类器] / [决策树] 算法 的简单说明 / [graphviz] 绘制决策树
目录
Python 机器学习 基础 之 监督学习 [朴素贝叶斯分类器] / [决策树] 算法 的简单说明 / [graphviz] 绘制决策树
一、简单介绍
二、监督学习 算法 说明前的 数据集 说明
三、监督学习 之 朴素贝叶斯分类器
四、监督学习 之 决策树
1、构造决策树
2、控制决策树的复杂度
3、分析决策树
4、树的特征重要性
附录
一、绘制决策树原理图的代码:鸢尾花数据集训练 的决策树模型的图形表示
二、如果报错 ModuleNotFoundError: No module named 'graphviz'
三、参考文献
一、简单介绍
Python是一种跨平台的计算机程序设计语言。是一种面向对象的动态类型语言,最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。Python是一种解释型脚本语言,可以应用于以下领域: Web 和 Internet开发、科学计算和统计、人工智能、教育、桌面界面开发、软件开发、后端开发、网络爬虫。
Python 机器学习是利用 Python 编程语言中的各种工具和库来实现机器学习算法和技术的过程。Python 是一种功能强大且易于学习和使用的编程语言,因此成为了机器学习领域的首选语言之一。Python 提供了丰富的机器学习库,如Scikit-learn、TensorFlow、Keras、PyTorch等,这些库包含了许多常用的机器学习算法和深度学习框架,使得开发者能够快速实现、测试和部署各种机器学习模型。
Python 机器学习涵盖了许多任务和技术,包括但不限于:
- 监督学习:包括分类、回归等任务。
- 无监督学习:如聚类、降维等。
- 半监督学习:结合了有监督和无监督学习的技术。
- 强化学习:通过与环境的交互学习来优化决策策略。
- 深度学习:利用深度神经网络进行学习和预测。
通过 Python 进行机器学习,开发者可以利用其丰富的工具和库来处理数据、构建模型、评估模型性能,并将模型部署到实际应用中。Python 的易用性和庞大的社区支持使得机器学习在各个领域都得到了广泛的应用和发展。
二、监督学习 算法 说明前的 数据集 说明
相关说明可见如下链接的 < 二、监督学习 算法 说明前的 数据集 说明 >,这里不在赘述:
数据集 说明:Python 机器学习 基础 之 监督学习 K-NN (K-邻近)算法 的简单说明-CSDN博客
三、监督学习 之 朴素贝叶斯分类器
朴素贝叶斯分类器是与上一节介绍的线性模型非常相似的一种分类器,但它的训练速度往往更快。这种高效率所付出的代价是,朴素贝叶斯模型的泛化能力要比线性分类器(如 LogisticRegression 和 LinearSVC )稍差。
朴素贝叶斯模型如此高效的原因在于,它通过单独查看每个特征来学习参数,并从每个特征中收集简单的类别统计数据。scikit-learn 中实现了三种朴素贝叶斯分类器: GaussianNB 、BernoulliNB 和 MultinomialNB 。GaussianNB 可应用于任意连续数据,而 BernoulliNB 假定输入数据为二分类数据,MultinomialNB 假定输入数据为计数数据(即每个特征代表某个对象的整数计数,比如一个单词在句子里出现的次数)。BernoulliNB 和 MultinomialNB 主要用于文本数据分类。
朴素贝叶斯分类器(Naive Bayes Classifier)是一种常用的监督学习算法,它基于贝叶斯定理和特征之间的条件独立性假设,用于解决分类问题。朴素贝叶斯分类器是一种简单而有效的分类算法,尤其在文本分类和垃圾邮件过滤等领域应用广泛。
基本原理
朴素贝叶斯分类器基于贝叶斯定理:
其中,𝑃(𝑌∣𝑋) 是在给定特征 𝑋 的条件下目标变量 𝑌 的概率,𝑃(𝑋∣𝑌) 是在给定目标变量 𝑌 的条件下特征 𝑋 的概率,𝑃(𝑌) 是目标变量 𝑌 的先验概率,𝑃(𝑋) 是特征 𝑋 的先验概率。
朴素贝叶斯分类器假设特征之间是条件独立的,即给定目标变量的情况下,特征之间没有关联。基于这个假设,我们可以将 𝑃(𝑋∣𝑌) 展开为特征之间的联合概率:
𝑃(𝑋∣𝑌)=𝑃(𝑥1∣𝑌)⋅𝑃(𝑥2∣𝑌)⋅…⋅𝑃(𝑥𝑛∣𝑌)
其中,𝑥1,𝑥2,…,𝑥𝑛 是特征。
应用
朴素贝叶斯分类器通常用于文本分类、垃圾邮件过滤、情感分析等任务。在文本分类任务中,朴素贝叶斯分类器可以根据文档中的单词频率来预测文档所属的类别。在垃圾邮件过滤任务中,朴素贝叶斯分类器可以根据邮件的内容和特征(如单词、语法结构等)来判断是否为垃圾邮件。
优点
- 简单高效:朴素贝叶斯分类器是一种简单而高效的分类算法,适用于大规模数据集。
- 适用性广泛:朴素贝叶斯分类器在文本分类、垃圾邮件过滤等领域应用广泛,并且在某些情况下表现良好。
缺点
- 对输入数据的分布假设过于简单:朴素贝叶斯分类器假设特征之间是条件独立的,这个假设在某些情况下可能不成立,导致模型的性能下降。
- 需要处理缺失值:朴素贝叶斯分类器需要对缺失值进行处理,否则可能影响模型的性能。
- 对输入数据的质量要求较高:朴素贝叶斯分类器对输入数据的质量要求较高,需要进行特征选择和预处理,否则可能影响模型的性能。
尽管朴素贝叶斯分类器存在一些缺点,但它仍然是一种常用的分类算法,特别适用于文本分类等领域。
BernoulliNB 分类器计算每个类别中每个特征不为 0 的元素个数。用一个例子来说明会很容易理解:
import numpy as np
X = np.array([[0, 1, 0, 1],
[1, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 1, 0]])
y = np.array([0, 1, 0, 1])这里我们有 4 个数据点,每个点有 4 个二分类特征。一共有两个类别:0 和 1。对于类别 0(第 1、3 个数据点),第一个特征有 2 个为零、0 个不为零,第二个特征有 1 个为零、1 个不为零,以此类推。然后对类别 1 中的数据点计算相同的计数。计算每个类别中的非零元素个数,大体上看起来像这样:
counts = {}
for label in np.unique(y):
# 对每个类别进行遍历
# 计算(求和)每个特征中1的个数
counts[label] = X[y == label].sum(axis=0)
print("Feature counts:\n{}".format(counts))
另外两种朴素贝叶斯模型(MultinomialNB 和 GaussianNB )计算的统计数据类型略有不同。 MultinomialNB 计算每个类别中每个特征的平均值,而 GaussianNB 会保存每个类别中每个特征的平均值和标准差。
要想做出预测,需要将数据点与每个类别的统计数据进行比较,并将最匹配的类别作为预测结果。有趣的是,MultinomialNB 和 BernoulliNB 预测公式的形式都与线性模型完全相同。不幸的是,朴素贝叶斯模型 coef_ 的含义与线性模型稍有不同,因为 coef_ 不同于 w 。
MultinomialNB和BernoulliNB都只有一个参数alpha,用于控制模型复杂度。alpha的工作原理是,算法向数据中添加alpha这么多的虚拟数据点,这些点对所有特征都取正值。这可以将统计数据“平滑化”(smoothing)。alpha越大,平滑化越强,模型复杂度就越低。算法性能对alpha值的鲁棒性相对较好,也就是说,alpha值对模型性能并不重要。但调整这个参数通常都会使精度略有提高。
GaussianNB主要用于高维数据,而另外两种朴素贝叶斯模型则广泛用于稀疏计数数据,比如文本。MultinomialNB的性能通常要优于BernoulliNB,特别是在包含很多非零特征的数据集(即大型文档)上。朴素贝叶斯模型的许多优点和缺点都与线性模型相同。它的训练和预测速度都很快,训练过程也很容易理解。该模型对高维稀疏数据的效果很好,对参数的鲁棒性也相对较好。朴素贝叶斯模型是很好的基准模型,常用于非常大的数据集,在这些数据集上即使训练线性模型可能也要花费大量时间。
四、监督学习 之 决策树
决策树是广泛用于分类和回归任务的模型。本质上,它从一层层的 if/else 问题中进行学习,并得出结论。
这些问题类似于你在“20 Questions”游戏 中可能会问的问题。想象一下,你想要区分下面这四种动物:熊、鹰、企鹅和海豚。你的目标是通过提出尽可能少的 if/else 问题来得到正确答案。你可能首先会问:这种动物有没有羽毛,这个问题会将可能的动物减少到只有两种。如果答案是“有”,你可以问下一个问题,帮你区分鹰和企鹅。例如,你可以问这种动物会不会飞。如果这种动物没有羽毛,那么可能是海豚或熊,所以你需要问一个问题来区分这两种动物——比如问这种动物有没有鳍。
决策树是一种常用的监督学习算法,用于解决分类和回归问题。它是一种基于树结构的模型,通过对数据进行递归分割来构建树,并根据特征的条件来做出决策。
下图是一个基于 鸢尾花数据集训练 的决策树模型的图形表示。您可以在绘制的图形中看到决策树的每个节点、分割特征以及每个叶节点的类别标签:
基本原理
决策树的基本原理是通过对特征进行递归分割来构建树,使得每个叶节点都对应于一个类别或者一个数值。在构建决策树时,算法会选择一个特征,并根据该特征的取值将数据集分成不同的子集。然后,对每个子集重复这个过程,直到满足停止条件为止。停止条件可以是节点中的样本数量小于阈值、树的深度达到预先定义的最大深度等。
在决策树的每个节点上,算法会选择最优的特征来进行分割,通常使用信息增益(Entropy)或基尼不纯度(Gini Impurity)等指标来衡量分割的效果。信息增益表示在给定特征的条件下,将数据集分成不同类别所带来的信息增加量。基尼不纯度表示随机选取两个样本,它们属于不同类别的概率。
应用
决策树可以应用于分类和回归问题。在分类问题中,决策树可以根据特征的条件来预测样本的类别。在回归问题中,决策树可以根据特征的条件来预测样本的数值。
优点
- 易于理解和解释:决策树的结构直观清晰,易于理解和解释,可以帮助用户了解问题的本质。
- 适用性广泛:决策树可以处理多种类型的数据,包括连续型数据和分类型数据。
- 不需要特征缩放:决策树不需要对特征进行缩放,因此不受特征缩放的影响。
缺点
- 容易过拟合:决策树容易过拟合训练数据,特别是在处理高维数据和复杂数据集时。
- 稳定性差:决策树对数据的微小变化敏感,可能导致树的结构发生较大变化。
- 不稳定性:决策树是一种局部优化算法,可能导致生成的树结构不稳定,对于同一组数据可能生成不同的树结构。
尽管决策树有一些缺点,但它仍然是一种非常有用的监督学习算法,特别适用于解决简单的分类和回归问题,以及需要可解释性模型的场景。
这一系列问题可以表示为一棵决策树,如下图
import mglearn
import matplotlib.pyplot as plt
import os
os.environ["PATH"] += os.pathsep + r'D:\Program Files\Graphviz\bin/'
# 运行 plot_animal_tree 函数
mglearn.plots.plot_animal_tree()
plt.savefig('Images/04DecisionTree-01.png', bbox_inches='tight')
plt.show()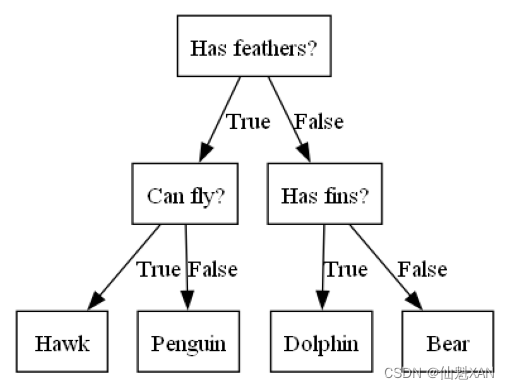
区分几种动物的决策树
在这张图中,树的每个结点代表一个问题或一个包含答案的终结点(也叫叶结点 )。树的边将问题的答案与将问的下一个问题连接起来。
用机器学习的语言来说就是,为了区分四类动物(鹰、企鹅、海豚和熊),我们利用三个特征(“有没有羽毛”“会不会飞”和“有没有鳍”)来构建一个模型。我们可以利用监督学习从数据中学习模型,而无需人为构建模型。
1、构造决策树
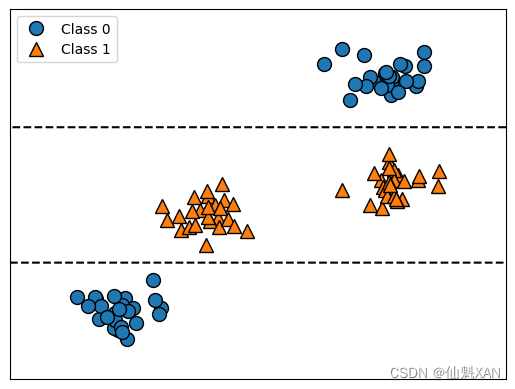
我们在下图 所示的二维分类数据集上构造决策树。这个数据集由 2 个半月形组成,每个类别都包含 50 个数据点。我们将这个数据集称为 two_moons 。
学习决策树,就是学习一系列 if/else 问题,使我们能够以最快的速度得到正确答案。在机器学习中,这些问题叫作测试 (不要与测试集弄混,测试集是用来测试模型泛化性能的数据)。数据通常并不是像动物的例子那样具有二元特征(是 / 否)的形式,而是表示为连续特征,比如下图所示的二维数据集。用于连续数据的测试形式是:“特征 i 的值是否大于 a ?”

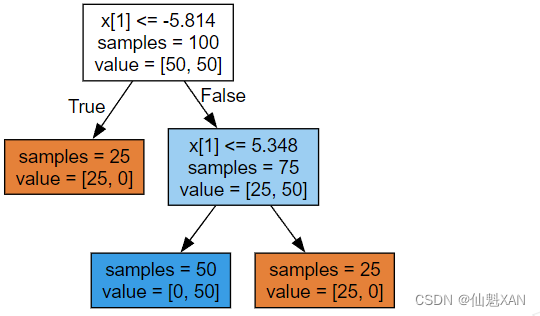
为了构造决策树,算法搜遍所有可能的测试,找出对目标变量来说信息量最大的那一个。下图展示了选出的第一个测试。将数据集在 x[1]=0.0596 处垂直划分可以得到最多信息,它在最大程度上将类别 0 中的点与类别 1 中的点进行区分。顶结点(也叫根结点 )表示整个数据集,包含属于类别 0 的 50 个点和属于类别 1 的 50 个点。通过测试 x[1] <= 0.0596 的真假来对数据集进行划分,在图中表示为一条黑线。如果测试结果为真,那么将这个点分配给左结点,左结点里包含属于类别 0 的 2 个点和属于类别 1 的 32 个点。否则将这个点分配给右结点,右结点里包含属于类别 0 的 48 个点和属于类别 1 的 18 个点。这两个结点对应于下图 中的顶部区域和底部区域。尽管第一次划分已经对两个类别做了很好的区分,但底部区域仍包含属于类别 0 的点,顶部区域也仍包含属于类别 1 的点。我们可以在两个区域中重复寻找最佳测试的过程,从而构建出更准确的模型。

下图 展示了信息量最大的下一次划分,这次划分是基于 x[0] 做出的,分为左右两个区域。
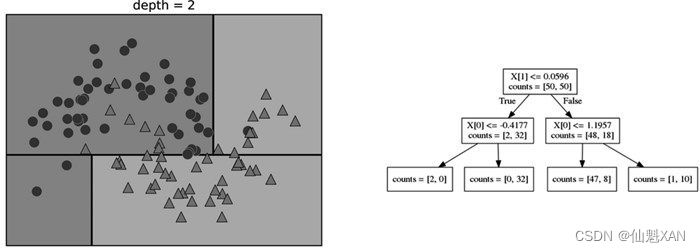
这一递归过程生成一棵二元决策树,其中每个结点都包含一个测试。或者你可以将每个测试看成沿着一条轴对当前数据进行划分。这是一种将算法看作分层划分的观点。由于每个测试仅关注一个特征,所以划分后的区域边界始终与坐标轴平行。
对数据反复进行递归划分,直到划分后的每个区域(决策树的每个叶结点)只包含单一目标值(单一类别或单一回归值)。如果树中某个叶结点所包含数据点的目标值都相同,那么这个叶结点就是纯的 (pure),这个数据集的最终划分结果见下图。
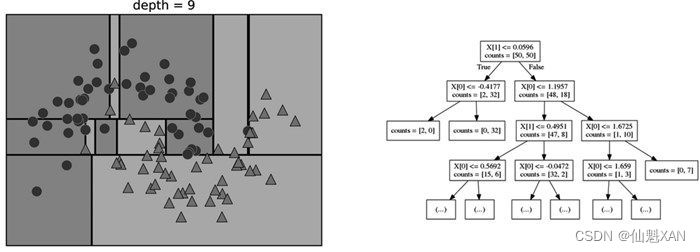
想要对新数据点进行预测,首先要查看这个点位于特征空间划分的哪个区域,然后将该区域的多数目标值(如果是纯的叶结点,就是单一目标值)作为预测结果。从根结点开始对树进行遍历就可以找到这一区域,每一步向左还是向右取决于是否满足相应的测试。
决策树也可以用于回归任务,使用的方法完全相同。预测的方法是,基于每个结点的测试对树进行遍历,最终找到新数据点所属的叶结点。这一数据点的输出即为此叶结点中所有训练点的平均目标值。
2、控制决策树的复杂度
通常来说,构造决策树直到所有叶结点都是纯的叶结点,这会导致模型非常复杂,并且对训练数据高度过拟合。纯叶结点的存在说明这棵树在训练集上的精度是 100%。训练集中的每个数据点都位于分类正确的叶结点中。在图 2-26 的左图中可以看出过拟合。你可以看到,在所有属于类别 0 的点中间有一块属于类别 1 的区域。另一方面,有一小条属于类别 0 的区域,包围着最右侧属于类别 0 的那个点。这并不是人们想象中决策边界的样子,这个决策边界过于关注远离同类别其他点的单个异常点。
防止过拟合有两种常见的策略:一种是及早停止树的生长,也叫预剪枝 (pre-pruning);另一种是先构造树,但随后删除或折叠信息量很少的结点,也叫后剪枝 (post-pruning)或 剪枝 (pruning)。预剪枝的限制条件可能包括限制树的最大深度、限制叶结点的最大数目,或者规定一个结点中数据点的最小数目来防止继续划分。
scikit-learn 的决策树在 DecisionTreeRegressor 类和 DecisionTreeClassifier 类中实现。scikit-learn 只实现了预剪枝,没有实现后剪枝。
我们在乳腺癌数据集上更详细地看一下预剪枝的效果。和前面一样,我们导入数据集并将其分为训练集和测试集。然后利用默认设置来构建模型,默认将树完全展开(树不断分支,直到所有叶结点都是纯的)。我们固定树的 random_state ,用于在内部解决平局问题:
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))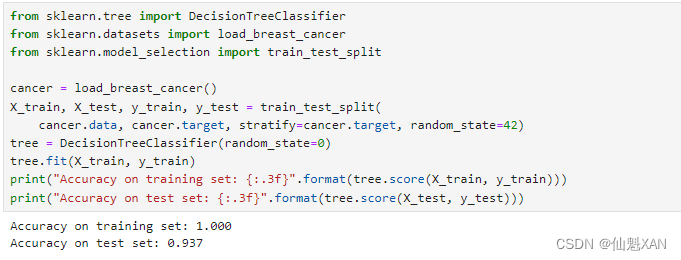
不出所料,训练集上的精度是 100%,这是因为叶结点都是纯的,树的深度很大,足以完美地记住训练数据的所有标签。测试集精度比之前讲过的线性模型略低,线性模型的精度约为 95%。
如果我们不限制决策树的深度,它的深度和复杂度都可以变得特别大。因此,未剪枝的树容易过拟合,对新数据的泛化性能不佳。现在我们将预剪枝应用在决策树上,这可以在完美拟合训练数据之前阻止树的展开。一种选择是在到达一定深度后停止树的展开。这里我们设置 max_depth=4 ,这意味着只可以连续问 4 个问题。限制树的深度可以减少过拟合。这会降低训练集的精度,但可以提高测试集的精度:
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("Accuracy on training set: {:.3f}".format(tree.score(X_train, y_train)))
print("Accuracy on test set: {:.3f}".format(tree.score(X_test, y_test)))
3、分析决策树
我们可以利用 tree 模块的 export_graphviz 函数来将树可视化。这个函数会生成一个 .dot 格式的文件,这是一种用于保存图形的文本文件格式。我们设置为结点添加颜色的选项,颜色表示每个结点中的多数类别,同时传入类别名称和特征名称,这样可以对树正确标记:
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["malignant","benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)我们可以利用 graphviz 模块读取这个文件并将其可视化(你也可以使用任何能够读取 .dot 文件的程序)
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
# 创建一个Graphviz的Source对象
source = graphviz.Source(dot_graph)
# 使用render方法将DOT转换为PNG(这需要使用Graphviz的命令行工具)
# render方法会返回一个表示输出文件名的字符串
output_filename = source.render("Images/04DecisionTree-02", format="png", view=True)
print(f"图片已保存为: {output_filename}")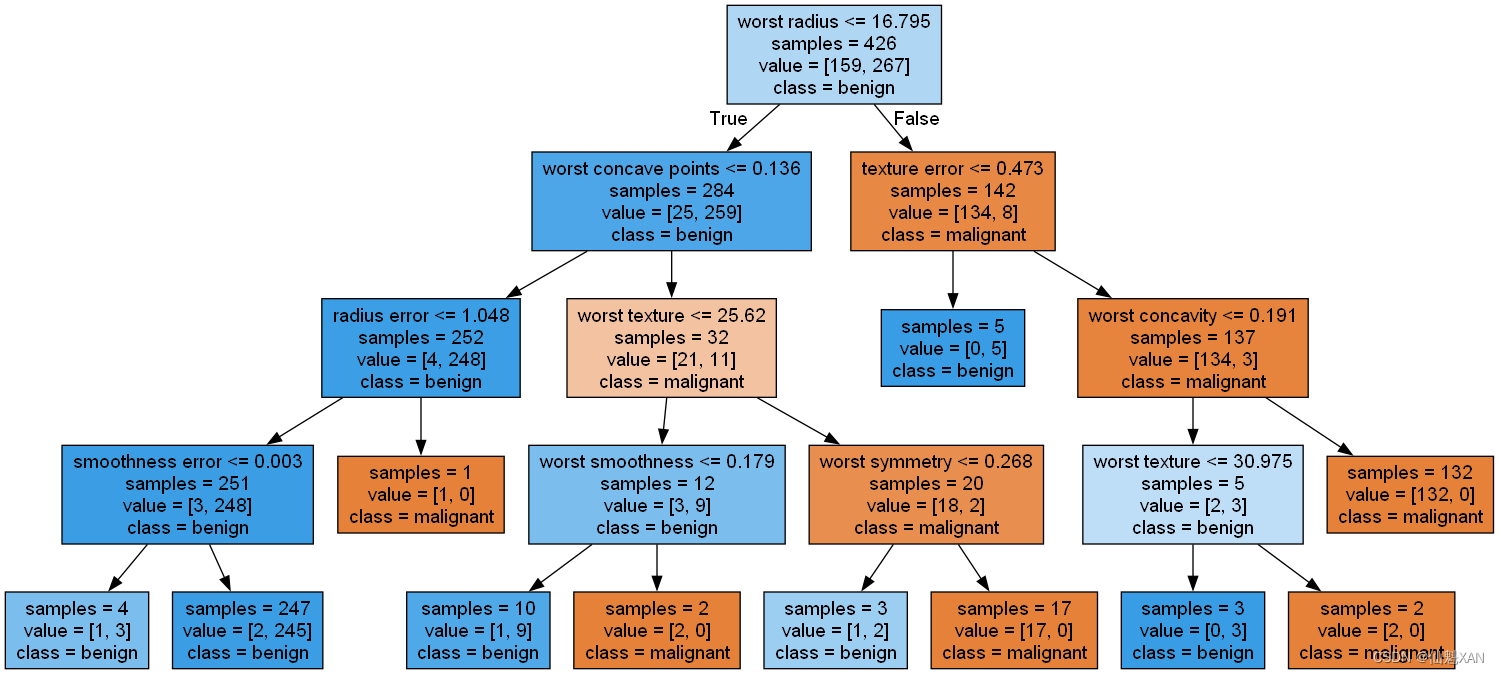
树的可视化有助于深入理解算法是如何进行预测的,也是易于向非专家解释的机器学习算法的优秀示例。不过,即使这里树的深度只有 4 层,也有点太大了。深度更大的树(深度为 10 并不罕见)更加难以理解。一种观察树的方法可能有用,就是找出大部分数据的实际路径。上图中每个结点的 samples 给出了该结点中的样本个数,values 给出的是每个类别的样本个数。观察 worst radius <= 16.795 分支右侧的子结点,我们发现它只包含 8 个良性样本,但有 134 个恶性样本。树的这一侧的其余分支只是利用一些更精细的区别将这 8 个良性样本分离出来。在第一次划分右侧的 142 个样本中,几乎所有样本(132 个)最后都进入最右侧的叶结点中。
再来看一下根结点的左侧子结点,对于 worst radius > 16.795 ,我们得到 25 个恶性样本和 259 个良性样本。几乎所有良性样本最终都进入左数第二个叶结点中,大部分其他叶结点都只包含很少的样本。
4、树的特征重要性
查看整个树可能非常费劲,除此之外,我还可以利用一些有用的属性来总结树的工作原理。其中最常用的是特征重要性 (feature importance),它为每个特征对树的决策的重要性进行排序。对于每个特征来说,它都是一个介于 0 和 1 之间的数字,其中 0 表示“根本没用到”,1 表示“完美预测目标值”。特征重要性的求和始终为 1:
print("Feature importances:\n{}".format(tree.feature_importances_))
我们可以将特征重要性可视化,与我们将线性模型的系数可视化的方法类似
import numpy as np
def plot_feature_importances_cancer(model):
n_features = cancer.data.shape[1]
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), cancer.feature_names)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plot_feature_importances_cancer(tree)
plt.savefig('Images/04DecisionTree-03.png', bbox_inches='tight')
plt.show()
这里我们看到,顶部划分用到的特征(“worst radius”)是最重要的特征。这也证实了我们在分析树时的观察结论,即第一层划分已经将两个类别区分得很好。
但是,如果某个特征的 feature_importance_ 很小,并不能说明这个特征没有提供任何信息。这只能说明该特征没有被树选中,可能是因为另一个特征也包含了同样的信息。
与线性模型的系数不同,特征重要性始终为正数,也不能说明该特征对应哪个类别。特征重要性告诉我们“worst radius”(最大半径)特征很重要,但并没有告诉我们半径大表示样本是良性还是恶性。事实上,在特征和类别之间可能没有这样简单的关系,你可以在下面的例子中看出这一点
tree = mglearn.plots.plot_tree_not_monotone()
display(tree)
plt.savefig('Images/04DecisionTree-04.png', bbox_inches='tight')Feature importances: [0. 1.]
该图显示的是有两个特征和两个类别的数据集。这里所有信息都包含在 X[1] 中,没有用到 X[0] 。但 X[1] 和输出类别之间并不是单调关系,即我们不能这么说:“较大的 X[1] 对应类别 0,较小的 X[1] 对应类别 1”(反之亦然)。
虽然我们主要讨论的是用于分类的决策树,但对用于回归的决策树来说,所有内容都是类似的,在 DecisionTreeRegressor 中实现。回归树的用法和分析与分类树非常类似。但在将基于树的模型用于回归时,我们想要指出它的一个特殊性质。DecisionTreeRegressor (以及其他所有基于树的回归模型)不能外推 (extrapolate),也不能在训练数据范围之外进行预测。
我们利用计算机内存(RAM)历史价格的数据集来更详细地研究这一点。图 2-31 给出了这个数据集的图像,x 轴为日期,y 轴为那一年 1 兆字节(MB)RAM 的价格:
import pandas as pd
ram_prices = pd.read_csv("data/ram_price.csv")
plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("Year")
plt.ylabel("Price in $/Mbyte")
plt.savefig('Images/04DecisionTree-05.png', bbox_inches='tight')
plt.show()
注意 y 轴的对数刻度。在用对数坐标绘图时,二者的线性关系看起来非常好,所以预测应该相对比较容易,除了一些不平滑之处之外。
我们将利用 2000 年前的历史数据来预测 2000 年后的价格,只用日期作为特征。我们将对比两个简单的模型:DecisionTreeRegressor 和 LinearRegression 。我们对价格取对数,使得二者关系的线性相对更好。这对 DecisionTreeRegressor 不会产生什么影响,但对 LinearRegression 的影响却很大。训练模型并做出预测之后,我们应用指数映射来做对数变换的逆运算。为了便于可视化,我们这里对整个数据集进行预测,但如果是为了定量评估,我们将只考虑测试数据集:
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
import numpy as np
# 利用历史数据预测2000年后的价格
data_train = ram_prices[ram_prices.date < 2000]
data_test = ram_prices[ram_prices.date >= 2000]
# 基于日期来预测价格
X_train = data_train.date.values.reshape(-1, 1) # 转换为 NumPy 数组并改变形状
# 我们利用对数变换得到数据和目标之间更简单的关系
y_train = np.log(data_train.price)
tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)
# 对所有数据进行预测
X_all = ram_prices.date.values.reshape(-1, 1) # 转换为 NumPy 数组并改变形状
pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)
# 对数变换逆运算
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)这里创建的将决策树和线性回归模型的预测结果与真实值进行对比:
plt.semilogy(data_train.date, data_train.price, label="Training data")
plt.semilogy(data_test.date, data_test.price, label="Test data")
plt.semilogy(ram_prices.date, price_tree, label="Tree prediction")
plt.semilogy(ram_prices.date, price_lr, label="Linear prediction")
plt.legend()
plt.savefig('Images/04DecisionTree-06.png', bbox_inches='tight')
plt.show()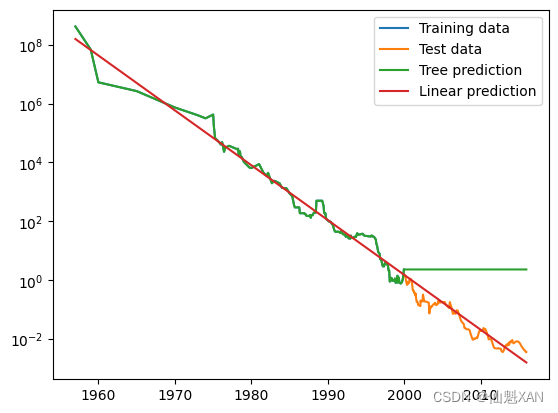
两个模型之间的差异非常明显。线性模型用一条直线对数据做近似,这是我们所知道的。这条线对测试数据(2000 年后的价格)给出了相当好的预测,不过忽略了训练数据和测试数据中一些更细微的变化。与之相反,树模型完美预测了训练数据。由于我们没有限制树的复杂度,因此它记住了整个数据集。但是,一旦输入超出了模型训练数据的范围,模型就只能持续预测最后一个已知数据点。树不能在训练数据的范围之外生成“新的”响应。所有基于树的模型都有这个缺点。
优点、缺点和参数
如前所述,控制决策树模型复杂度的参数是预剪枝参数,它在树完全展开之前停止树的构造。通常来说,选择一种预剪枝策略(设置
max_depth、max_leaf_nodes或min_samples_leaf)足以防止过拟合。与前面讨论过的许多算法相比,决策树有两个优点:一是得到的模型很容易可视化,非专家也很容易理解(至少对于较小的树而言);二是算法完全不受数据缩放的影响。由于每个特征被单独处理,而且数据的划分也不依赖于缩放,因此决策树算法不需要特征预处理,比如归一化或标准化。特别是特征的尺度完全不一样时或者二元特征和连续特征同时存在时,决策树的效果很好。
决策树的主要缺点在于,即使做了预剪枝,它也经常会过拟合,泛化性能很差。因此,在大多数应用中,往往使用下面介绍的集成方法来替代单棵决策树。
附录
一、绘制决策树原理图的代码:鸢尾花数据集训练 的决策树模型的图形表示
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
# 构建决策树模型
clf = DecisionTreeClassifier()
clf.fit(X, y)
# 绘制决策树
plt.figure(figsize=(10, 8))
plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, fontsize=10)
plt.savefig('Images/04DecisionTree-00.png', bbox_inches='tight')
plt.show()二、如果报错 ModuleNotFoundError: No module named 'graphviz'
如下图:
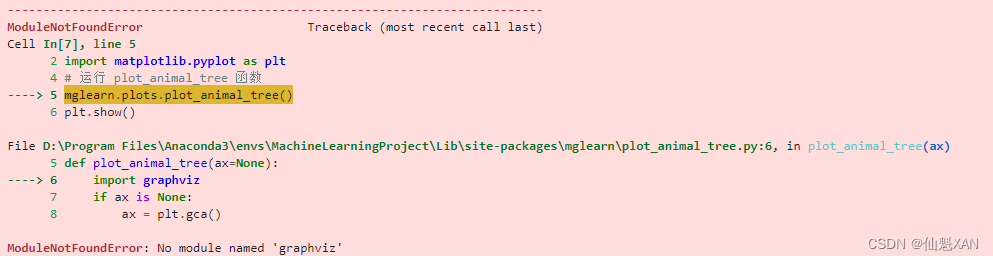
1)Graphviz的官网下载:Download | Graphviz,下载后按照提示进行安装就可以了
下载地址:Download | Graphviz
2)可以安装 graphviz 解决: pip install graphviz

3)配置路径 PATH
如果运行时报错的话,配置一下安装路径
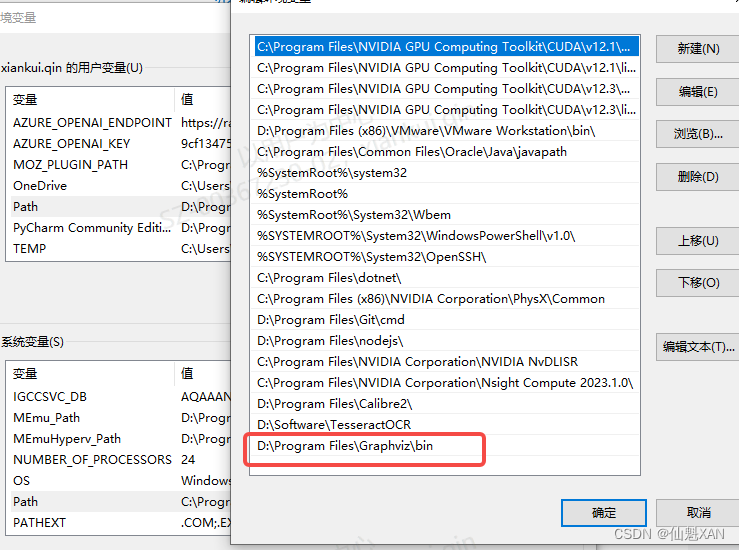
4)如果还报错,最后代码中添加如下代码
import os
os.environ["PATH"] += os.pathsep + r'你的Graphviz/bin路径位置' # 例如:D:\Program Files\Graphviz\bin/三、参考文献
参考文献:[德] Andreas C. Müller [美] Sarah Guido 《Python Machine Learning Basics Tutorial》