一篇文章告诉你聚类算法的作用和怎么用聚类算法！建议收藏！（下篇）

news2024/11/21 2:35:15

EM聚类

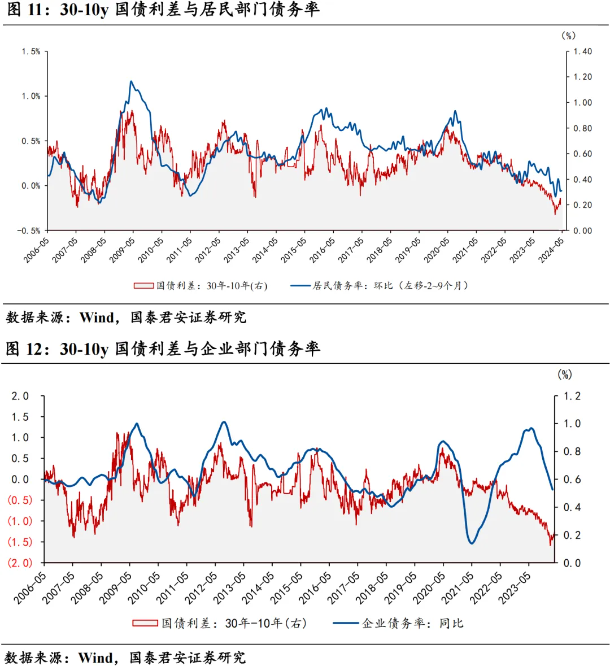
EM聚类基于概率分布对数据进行建模，通过迭代的期望和最大化步骤来估计模型参数，并将数据分为不同的聚类。EM聚类通常用于处理混合分布的数据，其中每个聚类被建模为一个概率分布。

原理介绍

EM聚类的核心思想是将数据集中的每个样本视为来自于一个潜在的分布（通常是多元高斯分布）的观测结果。该算法迭代地执行两个步骤：

1、Expectation Step（E步骤）：在这一步中，计算每个样本属于每个聚类的概率，即计算后验概率。这一步使用当前估计的模型参数（均值和协方差矩阵）来计算后验概率。

2、Maximization Step（M步骤）：在这一步中，基于E步骤中计算得到的后验概率，更新模型的参数，包括均值和协方差矩阵，以使似然函数最大化。这一步是一个最大似然估计（MLE）步骤。

重复执行E步骤和M步骤，直到收敛或达到预定的迭代次数。

最终，每个样本将被分配到一个聚类中，同时模型的参数将收敛到使数据最可能的参数值。

公式表达

EM聚类的主要数学公式涉及多元高斯分布。假设有个聚类，每个聚类被建模为一个多元高斯分布：

1、多元高斯分布：

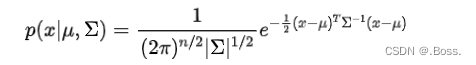
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture

# 生成一个随机的大型数据集
X, _ = make_blobs(n_samples=2000, centers=4, random_state=42)

# 使用EM聚类
gmm = GaussianMixture(n_components=4, random_state=42)
labels = gmm.fit_predict(X)

# 可视化结果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap="viridis")
plt.title("EM Clustering Result")
plt.show()

模糊聚类

模糊聚类与传统的硬聚类方法（如K均值）不同，它允许数据点属于多个不同的聚类，而不是仅属于一个确定的聚类。

模糊聚类通常使用模糊集合理论来描述数据点与聚类的隶属度（membership degree），因此也称为模糊C均值（Fuzzy C-Means，FCM）算法。

原理介绍

模糊聚类的目标是将数据点划分为多个模糊聚类，每个数据点可以与每个聚类关联一个隶属度，表示其属于该聚类的程度。这个隶属度通常在0到1之间，0表示不属于聚类，1表示完全属于聚类。

FCM的主要思想是最小化数据点与聚类中心之间的加权欧氏距离的平方，其中权重是隶属度的幂。这可以用以下公式表示：

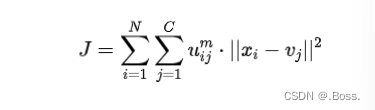
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score, calinski_harabasz_score, davies_bouldin_score, adjusted_rand_score

from fcmeans import FCM

# 生成模拟数据
n_samples = 3000
n_features = 2
n_clusters = 4
X, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用FCM进行模糊聚类
fcm = FCM(n_clusters=n_clusters)
fcm.fit(X_scaled)

# 获取聚类标签
fuzzy_labels = np.argmax(fcm.u, axis=1)

# 绘制模糊聚类结果
plt.figure(figsize=(10, 6))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=fuzzy_labels, cmap='viridis', s=50, alpha=0.5)
plt.scatter(fcm.centers[:, 0], fcm.centers[:, 1], marker='X', c='red', s=200, label='Cluster Centers')
plt.title('Fuzzy Clustering with FCM')
plt.legend()
plt.show()

# 计算模糊聚类的轮廓系数
silhouette_avg = silhouette_score(X_scaled, fuzzy_labels)
print(f'Silhouette Score: {silhouette_avg}')

# 计算每个数据点的轮廓系数
silhouette_values = silhouette_samples(X_scaled, fuzzy_labels)

# 绘制轮廓系数图
plt.figure(figsize=(8, 6))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=fuzzy_labels, cmap='viridis', s=50, alpha=0.5)
plt.title('Silhouette Plot for Fuzzy Clustering')
plt.xlabel('Silhouette Coefficient Values')
plt.ylabel('Cluster Labels')
plt.colorbar()
plt.show()

首先生成模拟数据，然后使用FCM进行模糊聚类。

然后计算了轮廓系数、Calinski-Harabasz指数、Davies-Bouldin指数和调整兰德指数（如果有真实标签）。

最后，绘制了模糊聚类结果的散点图和轮廓系数图，以可视化评估聚类质量。

注意：需要提前安装scikit-learn、matplotlib、numpy、fcmeans等