本文深入探讨了Nurbs曲线的概念、原理及应用,揭示了其在数字设计领域的独特价值和广泛影响。Nurbs曲线作为一种强大的数学工具,为设计师们提供了更加灵活、精确的曲线创建方式,从而极大地提升了设计作品的质感和表现力。文章首先介绍了Nurbs曲线的基本概念和数学原理,进而分析了其在工业设计、动画制作、3D打印等领域的实际应用。此外,文章还探讨了Nurbs曲线的未来发展前景,以及它如何继续推动数字设计领域的创新和进步。
1. 基本理论
NURBS是非均匀有理B样条(Non-Uniform Rational B-Splines)的缩写。
学习得从更特殊的形式学起,否则会比较懵。来看看各种曲线的关系图。
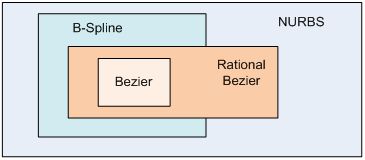
所以,似乎先学贝塞尔曲线应该是个好的开始。

2. 代码实现
辅助结构体定义
struct ColOfMatrix {
int32_t start_;
int32_t end_;
std::vector<double> vec_;
ColOfMatrix() : start_(-1), end_(0) {
}
};分割参数空间
template<class Point3_T>
bool splitParamSpace(const std::vector<Point3_T> &vInputPoint,
const std::vector<int> &vDPIndex,
std::vector<float> &vU,
std::vector<float> &vKnot) const {
bool bRet = true;
if (vInputPoint.empty() || vDPIndex.empty()) {
LOG(ERROR) << "vInputPoint.size() = " << vInputPoint.size() << ", vDPIndex.size() = " << vDPIndex.size();
bRet = false;
} else if (vDPIndex.front() != 0 || vDPIndex.back() != static_cast<int>(vInputPoint.size()) - 1) {
LOG(ERROR) << "The first and last element of vDPIndex is: " << vDPIndex.front() << ", " << vDPIndex.back()
<< "vInputPoint.size() = " << vInputPoint.size();
bRet = false;
} else {
int32_t numDistance = static_cast<int>(vInputPoint.size()) - 1;
std::vector<float> vDistance;
vDistance.reserve(numDistance);
double tmpDistance, tmpDiff;
for (auto first = vInputPoint.begin(), second = first + 1; second < vInputPoint.end(); ++first, ++second) {
tmpDiff = first->x - second->x;
tmpDistance = tmpDiff * tmpDiff;
tmpDiff = first->z - second->z;
tmpDistance += tmpDiff * tmpDiff;
vDistance.emplace_back(std::sqrt(tmpDistance));
}
double sumDistance = std::accumulate(vDistance.begin(), vDistance.end(), 0.f);
//Generate the vector U, U is u bar
vU.clear();
vU.reserve(vInputPoint.size());
if (sumDistance < 0.1f) {
LOG(ERROR) << "The line is too short.";
bRet = false;
} else {
double divisor = 1.f / sumDistance, elem(0);
for (auto it = vDistance.begin(); it < vDistance.end(); ++it) {
vU.emplace_back(elem);
elem += (*it) * divisor;
if (elem - 1.f > FLT_MIN) {
elem = 1.f;
}
}
vU.emplace_back(1.f);
}
if (bRet) {
//generate knot
vKnot.clear();
vKnot.reserve(vDPIndex.size() + 4u);
vKnot.emplace_back(0);
vKnot.emplace_back(0);
for (auto it = vDPIndex.begin(); it < vDPIndex.end(); ++it) {
vKnot.emplace_back(vU[*it]);
}
vKnot.emplace_back(1);
vKnot.emplace_back(1);
}
}
return bRet;
}计算控制点到曲线的映射矩阵
bool solveMatrixN(int32_t numCtrPoints,
const std::vector<double> &knot,
const std::vector<double> &U,
std::vector<ColOfMatrix> &matrixN) const {
int32_t numPoints = static_cast<int32_t>(U.size());
if (numCtrPoints > numPoints || knot.empty() || U.empty()) {
LOG(ERROR) << "The arguments is error in function solveMatrixN.";
return false;
}
int32_t degree = configPara_.order - 1;
matrixN.clear();
matrixN.resize(numCtrPoints);
int32_t index, s = degree;
std::vector<double> N; //It is a temporary variable
for (int32_t row = 0; row < numPoints; ++row) {
if (!findSpan(numCtrPoints - 1, s, U[row], knot, s)) {
return false;
}
if (!basisFun(s, U[row], degree, knot, N)) {
return false;
}
index = s - degree;
for (int32_t i = 0; i <= degree; ++i) {
if (matrixN[index + i].start_ == -1) {
matrixN[index + i].start_ = row;
}
matrixN[index + i].vec_.emplace_back(N[i]);
}
}
std::for_each(matrixN.begin(), matrixN.end(), [](ColOfMatrix &elem) {
elem.end_ = elem.start_ + static_cast<int32_t>(elem.vec_.size());
});
return true;
}求解控制点
template<class Point3_T>
bool solveCtrPoints(const std::vector<Point3_T> &inputPoints,
const std::vector<ColOfMatrix> &matrixN,
const std::vector<Point3_T> &R,
std::vector<Point3d> &ctrPoints) const {
//matrixN represent a matrix
if (inputPoints.empty() || matrixN.empty() || R.empty()) {
LOG(ERROR) << "The arguments are invalid in function solveCtrPoints.";
return false;
}
int32_t cols = static_cast<int32_t>(matrixN.size()); //Every element of matrixN is a column of a matrix
if (cols - 2 != static_cast<int32_t>(R.size())) {
LOG(ERROR) << "The vector R does not match the matrix NRIO";
return false;
}
//calculate (matrixN^T * matrixN)
cv::Mat squareMatrix = cv::Mat::zeros(cols, cols, CV_32F); // square matrix, squareMatrix = matrixN' * matrixN
auto itr = matrixN.begin();
for (int32_t r = 0; r < cols; ++r) // square matrix
{
auto p = squareMatrix.ptr<double>(r);
double tmp(0);
for (auto itCol = itr->vec_.begin(); itCol < itr->vec_.end(); ++itCol) {
tmp += (*itCol) * (*itCol);
}
p[r] = tmp
* 0.5f; // because it calculate a half of the matrix only, this function will sum this matrix and it's transposition
auto itc = itr + 1;
for (int32_t c = r + 1; c < cols; ++c) // square matrix
{
auto length = itr->end_ - itc->start_;
if (length <= 0) {
break;
} else if (length > static_cast<int32_t>(itc->vec_.size())) {
length = itc->vec_.size();
} else {
}
tmp = 0;
auto index = itc->start_ - itr->start_;
for (int32_t i = 0; i < length; ++i) {
tmp += itr->vec_[index] * itc->vec_[i];
++index;
}
p[c] = tmp;
++itc;
}
++itr;
}
squareMatrix = squareMatrix + squareMatrix.t();
cv::Rect center(1, 1, cols - 2, cols - 2);
cv::Mat sMatrix = squareMatrix(center);
//calculate (matrixN^T * matrixN)
sMatrix = sMatrix.inv(cv::DECOMP_LU);
//calculate control points. control points = squareMatrix*R
ctrPoints.clear();
ctrPoints.reserve(cols);
cols = sMatrix.cols;
Point3d tmpPoint, zeroPoint(0, 0, 0);
auto &point1 = inputPoints.front();
tmpPoint.x = point1.x;
tmpPoint.y = point1.y;
tmpPoint.z = point1.z;
ctrPoints.emplace_back(tmpPoint); //the first control point is the first point of the curve
for (int32_t i = 0; i < cols; ++i) {
tmpPoint = zeroPoint;
double *q = sMatrix.ptr<double>(i);
auto itR = R.begin();
for (int32_t j = 0; j < cols; ++j) {
const auto &element = q[j];
tmpPoint.x += itR->x * element;
tmpPoint.y += itR->y * element;
tmpPoint.z += itR->z * element;
++itR;
}
ctrPoints.emplace_back(tmpPoint);
}
auto &point2 = inputPoints.back();
tmpPoint.x = point2.x;
tmpPoint.y = point2.y;
tmpPoint.z = point2.z;
ctrPoints.emplace_back(tmpPoint); //the last control point is the last point of the curve
return true;
}计算RHS矩阵
template<class Point3_T>
bool generateR(const std::vector<ColOfMatrix> &matrixN,
const std::vector<Point3_T> &inputPoints,
std::vector<Point3_T> &R) const {
if (inputPoints.empty() || matrixN.empty()) {
LOG(ERROR) << "No input Points in generateR";
return false;
}
// It equal to the number of control Points. Every element of matrixN is a column of a matrix
int32_t cols = static_cast<int32_t>(matrixN.size());
if (cols < 2) {
LOG(ERROR) << "data error.";
return false;
}
int32_t rows = static_cast<int32_t>(inputPoints.size());
std::vector<Point3_T> Rmatrix(rows);
ColOfMatrix firstCol = matrixN.front(), lastCol = matrixN.back();
double element1, element2;
for (int32_t k = 1; k < rows - 1; ++k) {
if (k < firstCol.start_ || k >= firstCol.end_) {
element1 = 0;
} else {
element1 = firstCol.vec_[k - firstCol.start_];
}
if (k < lastCol.start_ || k >= lastCol.end_) {
element2 = 0;
} else {
element2 = lastCol.vec_[k - lastCol.start_];
}
//Rmatrix[k] = inputPoints[k] - element1 * inputPoints.front() - element2 * inputPoints.back()
Rmatrix[k] = subtract(inputPoints[k],
add(numericalMultiply(element1, inputPoints.front()),
numericalMultiply(element2, inputPoints.back())));
}
R.clear();
R.reserve(cols - 2);
auto itN = matrixN.begin() + 1;
int32_t startIdxN, endIdxN, startIdxR;
Point3_T tmpPoint;
for (int32_t i = 1; i < cols - 1; ++i) {
if (itN->start_ < 1) {
startIdxR = 1;
startIdxN = 1 - itN->start_;
} else {
startIdxR = itN->start_;
startIdxN = 0;
}
if (itN->end_ > rows - 1) {
endIdxN = rows - 1 - itN->start_;
} else {
endIdxN = itN->end_ - itN->start_;
}
auto it = Rmatrix.begin() + startIdxR;
reset(tmpPoint);
for (int32_t j = startIdxN; j < endIdxN; ++j) {
tmpPoint += numericalMultiply(itN->vec_[j], *it);
++it;
}
R.emplace_back(tmpPoint);
++itN;
}
return true;
}其它辅助函数
//This function is called frequently
bool basisFun(const int32_t s,
const double u,
const int32_t p,
const std::vector<double> &U,
std::vector<double> &N) const {
if (!U.empty()) {
std::vector<double> left(p + 1, 0.0f);
std::vector<double> right(p + 1, 0.0f);
N.clear();
N.resize(p + 1, 0.0f);
N[0] = 1.0f;
double saved, tmp;
for (int32_t j = 1; j <= p; ++j) {
left[j] = u - U[s + 1 - j];
right[j] = U[s + j] - u;
saved = 0.0f;
for (int32_t r = 0; r < j; ++r) {
tmp = N[r] / (right[r + 1] + left[j - r]);
N[r] = saved + right[r + 1] * tmp;
saved = left[j - r] * tmp;
}
N[j] = saved;
}
return true;
} else {
LOG(INFO) << "Input data are empty";
return false;
}
}
//This function is called frequently
bool findSpan(const int32_t n, const int32_t p, double u, const std::vector<double> &knot, int32_t &s) const {
if (n < static_cast<int32_t>(knot.size()) && p <= n) {
if (u < knot[p]) {
s = p;
} else if (u > knot[n]) {
s = n;
} else {
int32_t low = p;
int32_t high = n + 1;
int32_t mid = low + (high - low) / 2; // mid = floor((high+low)/2)
while (low + 1 < high) // +1 for low = high -1 case
{
if (u - knot[mid] < -FLT_MIN) {
high = mid;
} else if (u - knot[mid + 1] > -FLT_MIN) {
low = mid;
} else {
break;
}
mid = low + (high - low) / 2; // mid = floor((high+low)/2)
}
s = mid;
}
return true;
} else {
LOG(ERROR) << "The arguments are invalid in function findSpan.";
return false;
}
}重建
template<class Point3_T>
bool reconstruct(const NurbsParam &NURBSParam,
const float step,
std::vector<std::vector<Point3_T>> &vvOutPoints) const {
if (NURBSParam.vecCtrlPoint.empty() || step < FLT_EPSILON || step > NURBSParam.paintTotalLength / 3.0f) {
LOG(ERROR) << "The arguments are invalid in function reconstruct.";
return false;
}
int32_t outputPointNum = static_cast<int32_t>(std::ceil(NURBSParam.paintTotalLength / step));
// Safety guard
outputPointNum = std::max(outputPointNum, 2);
std::vector<int32_t> vecIdx;
vecIdx.reserve(NURBSParam.endPoint.size());
if (NURBSParam.endPoint.empty()) {
LOG(ERROR) << "The endPoint is empty.";
return false;
} else if ((NURBSParam.endPoint.size() & 0x1) != 0) {
LOG(ERROR) << "The number of end points must be even.";
return false;
} else {
for (auto it1 = NURBSParam.endPoint.begin(), it2 = it1 + 1; it2 < NURBSParam.endPoint.end(); ++it1, ++it2) {
if (*it1 > *it2) {
LOG(ERROR) << "The arguments are invalid in function generateCurve.";
return false;
}
}
for (auto it1 = NURBSParam.vecKnot.begin(), it2 = it1 + 1; it2 < NURBSParam.vecKnot.end(); ++it1, ++it2) {
if (*it1 > *it2) {
LOG(ERROR) << "The arguments are invalid in function generateCurve.";
return false;
}
}
}
float length(0); //the length of the paint
auto it = NURBSParam.endPoint.begin();
while (it < NURBSParam.endPoint.end()) {
length -= *(it++);
length += *(it++);
}
float scale = length / (outputPointNum - 1); // outputPointNum >= 2
if (scale < FLT_EPSILON) {
LOG(INFO) << "The input data are invalid.";
return false;
}
it = NURBSParam.endPoint.begin();
float tmp = *(it++);
std::vector<double> U;
U.reserve(outputPointNum);
int32_t i = 0;
while (it < NURBSParam.endPoint.end()) {
U.emplace_back(tmp);
++i;
tmp += scale;
// if tmp > the second end point of a segment, then set tmp as the first end point of next segment.
if (tmp > *it) {
U.emplace_back(*(it++));
vecIdx.emplace_back(++i);
if (it == NURBSParam.endPoint.end()) {
break;
} else {
tmp = *(it++);
}
}
}
std::vector<Point3_T> outputPoints;
if (!outSample(NURBSParam, U, outputPoints)) {
LOG(ERROR) << "Sample error";
return false;
}
vvOutPoints.clear();
vvOutPoints.resize(vecIdx.size());
auto begin = outputPoints.begin();
auto first = begin, last = begin;
for (size_t i = 0; i < vvOutPoints.size(); ++i) {
last = begin + vecIdx[i];
vvOutPoints[i].insert(vvOutPoints[i].end(), first, last);
first = last;
}
return true;
}参考文献
Nurbs曲线详解_123_jason的博客-CSDN博客_nurbs曲线
NURBS_百度百科
NURBS(一): 动机、定义以及历史漫谈 - Fun With GeometryFun With Geometry
NURBS(一)贝塞尔曲线 - 知乎
![[FlareOn1]Bob Doge](https://img-blog.csdnimg.cn/direct/71481679ba63477bbbd474a9027f3093.png)