• 文献标题：《Epipolar Geometry of Opti-Acoustic Stereo Imaging》
• 作者列表：Shahriar Negahdaripour
• 发表期刊：IEEE Transactions on Pattern Analysis and Machine Intelligence
• 发表年份：2007
• DOI链接：10.1109/TPAMI.2007.1092
  PS：在本文中，Epipolar geometry 翻译为 “对极几何” 或 “外极几何”，两者表达同一个意思。

摘要

光学和声呐相机是检查水下设备的合适成像系统，既可用于定期维护，也可用于安全操作。尽管光学系统具有高分辨率，但是部署在浑浊水域时，其可视范围受限。相比之下，新一代高频（MHz）前扫声呐相机虽然在射程上比传统的低频或中频（10s-100s KHz）声呐系统缩短了一到两个数量级，但却能在高度浑浊的水域中提供更清晰的目标图像。可以想象，一种有效的检测策略是在潜水平台上同时部署光学和声呐相机，以便在各种浑浊度条件在对目标进行成像。在这种情况下，如果能见度允许，两台相机（以双目立体配置排列）的图像配准可提供有价值的场景信息，而这些信息无法单独从每个传感器中获取。在这篇文章中，我们利用这两种具有不同投影模型的感知模式探讨并推导了对极几何和立体三角测量的约束方程。计算机仿真得到的理论结果表明，光-声立体成像系统优于传统的光学相机双目视觉系统，尤其是在增加目标距离和/或浑浊度的情况下。

关键词：立体视觉、对极几何、三角测量、光学和声呐成像

1. 引言

配备成像系统的无人水下潜航器是自主检测船体和其他水下人造结构（如水坝、桥墩和管道）的有效平台[17]。光学相机可以在低浑浊度条件下提供目标表面的高精细图像，并且可以利用散射介质中的光偏振来扩大自然光照水下图像的可视范围[30]。不过，这些传感器在港口水域和其他高度浑浊的环境中可能会失效，这一缺点可以通过部署高分辨率前向扫描声呐相机来克服[3][15][33]。然而，由于声学杂波较多，在解释含噪声的声呐视频图像时往往会出现复杂问题。在能见度允许的情况下，与单独处理每个传感器的图像相比，融合光学和声学图像特征可提高系统性能。

最近，在多传感器融合和图像数据与已知三维物体模型配准方面[6][9]，以及在沿海底自然轮廓自动导航方面[1]，都对这一策略进行了探索，其关键优势在于利用3D声呐提供的有价值场景信息[37]。近年来，二维高频FS声呐相机，如1.1/1.8 MHz双频识别声纳(DIDSON)和450/900 KHz BlueView已投入商业使用。这些相机提供的视频图像具有足够高的细节，使得人类操作员能够识别视觉目标。传统的声呐成像系统工作频率在 10 到 100 KHz之间，射程达千米，而这些高频系统与之不同，射程不超过几十米，但这足以满足许多搜索和检查任务的需要，而这正是主要的目标应用[40]。虽然由人类操作员或潜水员进行部署非常有用，但更广泛的用途来自于计算机视觉方法的发展，该方法可以提供声呐图像的3D解释。

我们可以设想这样一种场景：一个潜水平台，配备了传统的光学相机作为操作人员可视化和远程控制的标准设备，还携带了一个二维成像声呐，用于在浑浊条件下进行可视化和目标成像。将这些系统配置为重叠视图，可有效提供双目立体视觉能力，并能恢复三维场景结构信息。

多视图几何为研究运动和立体视觉中的各种问题提供了统一的框架，例如标定和未标定相机、投影和非投影模型等[8], [14]。它还为机器视觉、计算机图形学、摄影测量学和医学成像等应用中由单传感器或全景成像系统生成的立体对和视图进行3D场景重建的众多方法奠定了基础[4]、[5]、[28]、[31]、[35]。对来自不同传感模式的图像进行处理和配准在医学领域很常见 [20][21][29]，然而，在这里，物体模型是利用来自单一成像设备的多个二维视图或体积图像构建的，然后用于与来自其他传感模式(如磁共振成像(MRI)、多普勒组织成像(DTI)等)的图像进行配准。其他方法可以将2D-2D或3D-3D配准方法集成到混合活检系统中，例如，合并活检前MRI信息和实时超声(US)图像，使患者处于与磁共振(MR)图像采集时相同的体位。利用信息论中的互信息最大化原理进行多模态医学图像配准的文献也非常丰富，例如 [41]、[42]、[43]。与我们的工作更直接相关的研究涉及透视图像、立体图像对以及全景图像的对极几何[19], [22], [26], [27], [36]。在选定的结果中，Seitz 和 Kim [27] 表明，外极几何仅限于平面、双曲抛物面和双曲抛物面族。

受水下成像和潜在医学成像中各种应用的启发，我们探索了光-声立体成像的外极几何，这是在立体配置中部署二维声呐和光学相机时产生的（见图1）。除了在建立特征对应关系和三维重建方面的应用外，外极几何还为潜水平台的自主地图导航奠定了基础，这也是水下结构自动检测领域另一项备受追捧的功能。本文的目的是利用几何约束来融合目标的视觉和声学特征，以解决图像-模型配准问题，实现自主定位。

图1 （a）平行和（b）汇聚相机的立体几何。（c） 汇聚相机典型配置的各种参数之间的关系

需要指出的是，correspondence问题、外参标定和最佳三维重建解决方案的推导是将这种新型多模态传感技术用于物体重建和建模的主要挑战。我们目前正在研究correspondence问题，并在其他地方[24]、[25]深入探讨了外参标定和三维重建问题。特别是，第4节中介绍的光声立体三角测量的各种解释有助于我们：1)量化所提出的技术相对于传统双目系统的优点；2)确定我们如何更有效地利用距离和方位角测量进行3D重建[25]。

我们强调，在设计出一种有效的通用方法之前，可以简化光声对应问题以便在各种受控情况下立即应用。例如，在人造环境中，我们可以为某些具有已知声反射特性的物体 "涂上 "独特的视觉特征（标记）。通过生成匹配的声学和视觉特征数据库，同时利用外极几何将匹配搜索限制在一个维度上，我们可以更容易地建立对应关系。在底栖(benthic)环境中，我们可以用声学反射器标记选定的感兴趣的自然物体（具有明显的视觉特征），这同样有助于在光声立体图像对中匹配相应的特征。此外，这些匹配结果可能会传播到附近没有标签的物体上[7]，[16]。在某些海洋科学应用中，在离线手动过程中进行匹配以重建某些目标特征以便记录可能就足够了。(尽管最近出现了自动化系统，如 [11]、[12]、[23] 等所使用的系统，但许多海洋科学研究仍依赖于手工产品，包括利用手工摄影测量软件工具对沉船和其他考古遗址进行mosaics，如[10])。在这里，使用对极几何再次帮助用户找到正确的匹配。最后，我们的研究结果还可以推广到信息融合至关重要的其他多模态传感器应用中，但与光-声成像相比，这些应用中的配准/匹配问题更容易解决。

本文其余内容安排如下： 在第 2 节中，我们介绍了二维光学和声呐成像的一些相关背景。我们还介绍了二维声呐相机的一些校准结果，主要目的是为二维声呐成像系统的投影模型提供一些启示。在第 3 节中，我们介绍了光声立体系统的投影方程，并建立了外极几何，即光学和声呐图像中的外极轮廓方程。这些结果适用于平行相机和汇聚相机以及其他任意配置的情况。我们还给出了各种理论结果的例子。在第 4 节中，我们介绍了光声成像背景下的立体三角测量，通过对这些结果的几何解释，我们可以更好地理解这种新型多模态立体成像技术的优点。第 5 节中的实验演示了真实数据集的外极点几何。第 6 节为结束语，第 7 节总结了我们的贡献。

2. 预备知识

2.1 符号定义

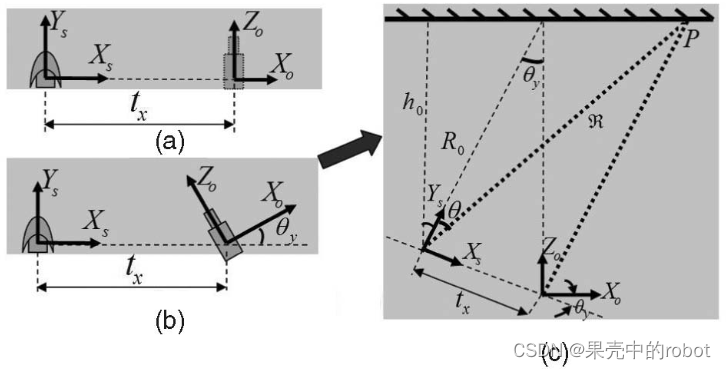
大多数参数和变量都是全局的。少数局部定义的参数和变量很容易从上下文中识别出来，因此我们在此仅列出全局参数。三维空间中的点用 $P=[X,Y,Z]$ 表示，而下标 $s$ 和 $o$ 分别代表声呐坐标系和光学相机坐标系中的测量值。光学图像中的点坐标为 $(x,y)$ ，声呐视图中的距离和方位角测量值用 $(\mathfrak{R},\theta )$，$\varphi$是一个三维点的仰角。声呐图像中的极线轮廓用直角坐标 $(x_s,y_s)=\mathfrak{R}(\sin \theta ,\cos \theta )$ 表示。旋转矩阵 $R$ 和平移向量 $t=[t_x,t_y,t_z{]}^T$ 表示声呐坐标系中的光学相机位姿。$R$ 的行、列和元素分别用 ${\mathbf{r}}_i,{\tilde{\mathbf{r}}}_i,r_{ij}$ 表示，($i,j=1:3$)。光学图像中的外极轮廓可以用元素为 $u_{ij}$ 的 $3\times 3$ 矩阵 $\mathbf{U}$ 来描述。$\mathbf{U}$ 的特征值为 ${\lambda }_i(i=1:3)$。最后，${\theta }_y$ 表示基线与光学相机坐标系 $X$ 轴之间的夹角。

2.2 坐标系定义

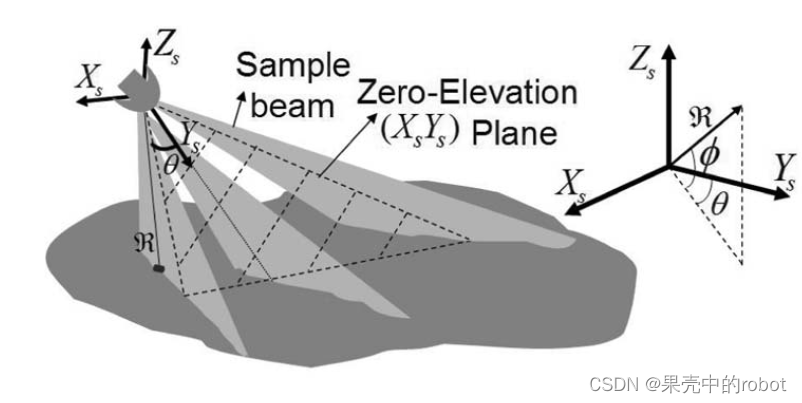
三维点 $P$ 可以分别用直角坐标 $[X,Y,Z{]}^T$ 和球坐标 $[\theta ,\varphi ,\mathfrak{R}{]}^T$ 表示。直角坐标系中的测量值为“横向距离”、“下向距离”和“高度”，而 $\theta$ 和 $\varphi$ 分别为方位角和仰角，$\mathfrak{R}$ 为距离。

图2 声呐投影和坐标系

参照图2，直角坐标与球坐标的关系为：

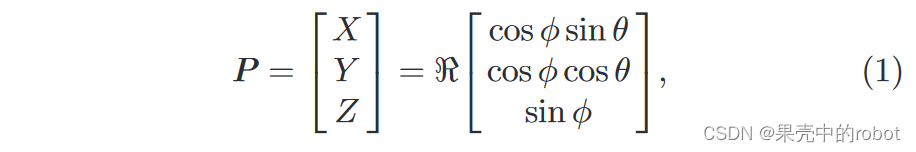
其中，该变换的逆变换为：

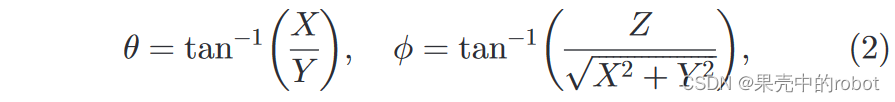
以及 $\mathfrak{R}=\sqrt{X^2+Y^2+Z^2}$。

2.3 FS声呐相机

声呐相机通过记录声脉冲对场景的反射声波来生成图像。在三维FS声呐中，例如Echoscope[37]，反向散射信号由二维换能器阵列收集，图像由“波束信号”(来自固定方向的回波)形成，由仰角$\varphi$和方位角$\theta$方向指定(见图2)。三维点的距离 $\mathfrak{R}$ 以波束信号的峰值为基础，根据声波的往返时间确定。

二维DIDSON相机使用 96 个波束，方位角宽度约为 $w_{\theta }$ = 0.3 [deg]，仰角宽度大约为 $w_{\varphi }$ = 14 [deg]，由声学透镜和换能器曲率形成。发射光束的水平间隔为 0.3 [度]，方位角方向的总覆盖范围为 28.8 [度]。图像 $I(\mathfrak{R},\theta )$ 基于每个波束在特定方位方向上的飞行时间(距离 $\mathfrak{R}$ )而形成的。波束的几何形状在方位角方向上提供了(相对)良好的定位精度。然而，将其作为二维成像系统处理主要是因为成像三维点的仰角有 $\pm$ 7 [度] 的不确定性。由于仰角维度的波束宽度有限，通常以相对较小的掠角观察场景表面。这就确保了每一帧都能覆盖更大的目标区域，从而更有可能以高声呐回波对某些物体特征进行成像。下视分辨率 (Downrange resolution, DR) 是根据可调节的下视窗口大小 $[{\mathfrak{R}}_{\min }-{\mathfrak{R}}_{\max }]$ [m] 内的总共 512 个范围值设置的，以便对相距声呐期望范围内的物体成像。在28.8 度的方位角方向视野内，横向距离范围大约为 0.5 * DR 米。图 3 展示了圣彼得堡港（佛罗里达州圣彼得堡）一处海脊的光学和声纳图像。

图3 佛罗里达州圣彼得堡港一处海脊的光学和声纳图像

2.4 声呐标定

虽然这一部分与本文的主要内容没有直接关系，但它提供了对二维声呐相机投影特性的更多了解。
对于一个完美的声学透镜，方位角和距离角可以很容易地转换为计算机坐标。也就是说，96个DIDSON光束中的每一个都可以根据线性变换公式 $\Omega =a_0+a_1\theta$ 对应到方位角（当工作在1.8MHz时，$a_1=3.3333$, $a_0=48.50$）。与光学传感器一样，声学透镜的缺陷也会导致图像失真，并与 (1) 中的理想投影模型产生几何偏差。这在图4a中很明显，图4a描绘了2D DIDSON声呐相机记录的已知校准网格的原始图像。图4b所示的校正图像是利用不同方向的网格成像，采用内参标定方法得到的[18]。在这种标定中，使用了 22 幅图像中的 765 个网格点，其中许多视图只覆盖了网格的一小部分[18]。图4a中的红色标记描绘了扭曲的网格角位置(来自选定图像的校准数据)。图4b中的红色标记是已知的三维网格点在校正后的图像上的投影，目的是直观地检验与理论投影模型的一致性。

图4 (a) DIDSON声呐的原始数据。（b）基于相机标定的矫正图像。（a）中标记的角是待校准的网格点，（b）中的标记表示投影到已校正图像上的已知 3D 网格点。

3. 对极几何

假设采用针孔相机模型，某个三维目标点 ${\mathbf{P}}_o=[X_o,Y_o,Z_o{]}^T$ 的光学图像坐标为 $\mathbf{p}=(x,y,f)$ 由以下公式给出：

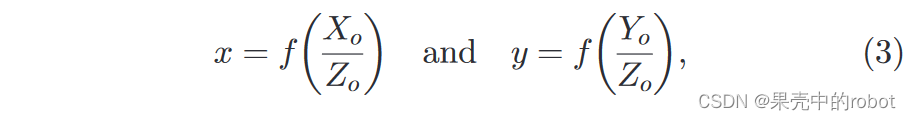
其中，$f$是光学相机的有效焦距，假定为单位长度。${\mathbf{P}}_s=[X_s,Y_s,Z_s{]}^T$ 表示三维点在声呐参考系下的坐标，光学图像点 $\mathbf{p}=(x,y,1)$ 在声学图像中的匹配点 $\mathbf{s}=(\theta ,\mathfrak{R})$ 给出了距离和方位角测量：

建立成对的对应关系是光学相机立体视觉的主要困难，如果要将声呐图像中的特征与光学图像中的相应特征进行匹配，复杂性就会变得更高。因此，建立光-声立体视觉系统的对极几何关系以将简化为一维搜索变得至关重要。通过对成像三维点的仰角施加边界（在DIDSON声呐相机中为 $\pm$ 7 度），搜索空间会变得更加受限。
在建立对极几何时，我们寻求所谓共轭对 $\mathbf{p}$ 和 $\mathbf{s}$ 之间的关系或约束：从一副图像中的任意一点开始，我们想要确定在另一个图像中对应点的位置。在传统的光学相机双目视觉中，这些匹配点位于外极线上，即外极平面与两台相机图像平面的交点上。由于光-声系统中的投影模型不对称，两个视图中的外极点几何形状也不同。光学图像中的外极曲线很容易被识别为圆锥曲线：这些是大圆在球面上的投影（与声呐距离为 $\mathfrak{R}$、方位角为 $\theta$的点的轨迹）。因此，每条曲线都是与由这些大圆的投影射线组成的圆锥的像平面的交点。如图 6a 所示，对于几乎平行配置的相机，圆锥截面为双曲线。然而，我们仍然需要确定是否/何时会出现其他的圆锥曲线。此外，声学图像中的几何图形无法通过观察轻易确定。正如我们将在第 3.1 节中看到的，潜在曲线的方程是通过对投影方程进行代数处理来确定的。

在从多个光学视图进行三维重建时，外极点（一个视图/摄像机的光学中心在另一个/多个视图/摄像机中的投影）往往起着关键作用。相比之下，这些点在光-声系统中的重要性并不明显。不过，如果将光学相机投影中心视为声学点源，我们可以在声呐视图中计算相应的距离和方位角测量：

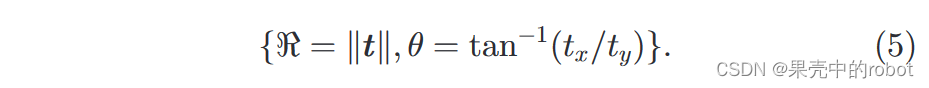
直角坐标形式 $(x_s,y_s)$ 是一种合适的表示方法，可以得到外极点 ${\mathbf{e}}_s$：

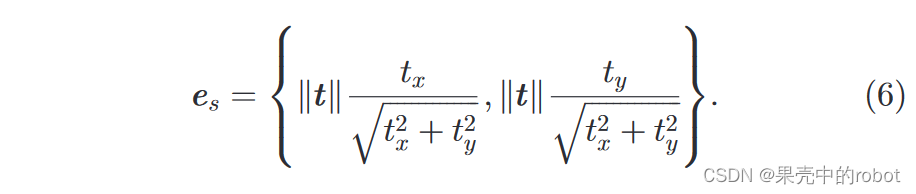
同样，声呐坐标系的原点投影到光学图像中的 ${\mathbf{e}}_o=-\mathbf{C}{\mathbf{R}}^T\mathbf{t}$ （这里 $\mathbf{C}$ 表示光学相机的投影矩阵[14]）。外极点 ${\mathbf{e}}_o$ 是测距球体（或者与不同方位平面关联的大圆）中心的投影。

3.1 声呐到光学相机的映射

给定 $P$ 点的声呐测量值 s = { θ , R } \bm{s}={\{\theta, \mathfrak{R}\}} s={θ,R}，我们在光学图像中寻找匹配点 $\mathbf{p}=(x,y,1)$ 的位置。为了确定这一点，我们利用两个参考系中三维点坐标 ${\mathbf{P}}_o$ 和 ${\mathbf{P}}_s$ 之间的关系：

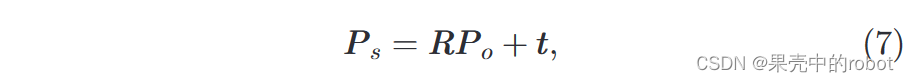
其中 $\mathbf{R}$ 是 $3\times 3$ 旋转矩阵，$\mathbf{t}=[t_x,t_y,t_z{]}^T$ 是位移向量，定义了两个坐标系之间的刚体变换。通过对选定的已知目标进行图像测量来确定 $\mathbf{R}$ 和 $\mathbf{t}$ 是外参标定问题[25]的一种应用，正如传统双目系统通常采用的方法[32]，这里只需要假设 $\mathbf{R}$ 和 $\mathbf{t}$ 已经确定即可。因此我们有：

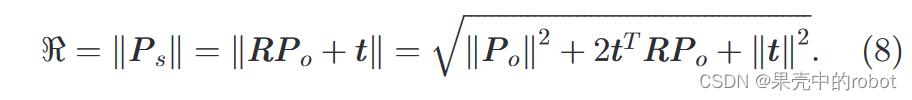
由此，我们可以写出：

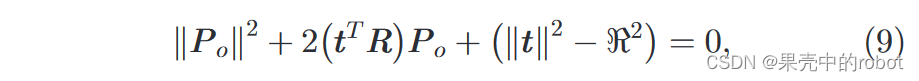
根据光学相机的图像坐标，可以得出：

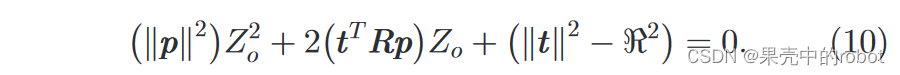
我们有：

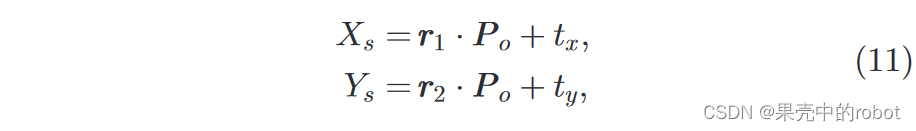
其中 ${\mathbf{r}}_i(i=1,2,3)$表示旋转矩阵的行。将其代入声呐方位角方程可以得出：

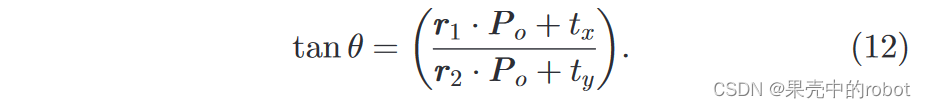
由此得出以下等式：

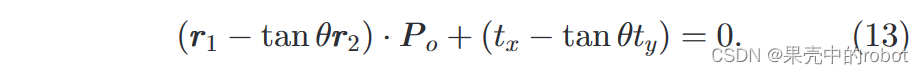
利用光学相机投影方程，我们可以得到：

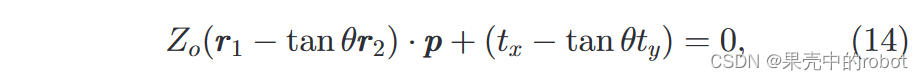
得出：

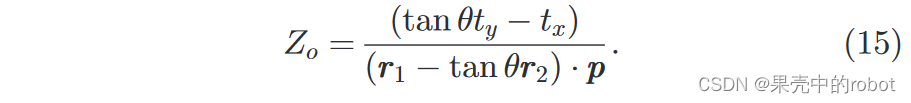
根据 (10)，我们可以得到所需的外极性约束条件：

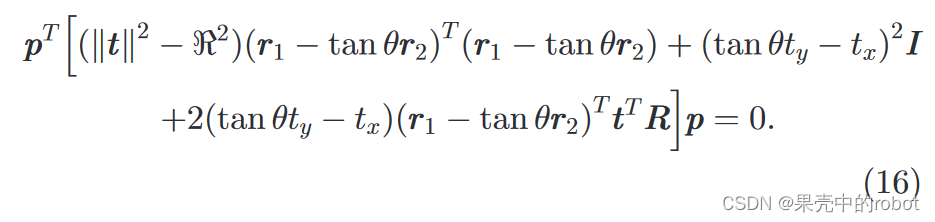
最后，我们通过加上它的转置将其写成对称形式：

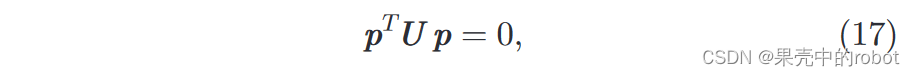
其中

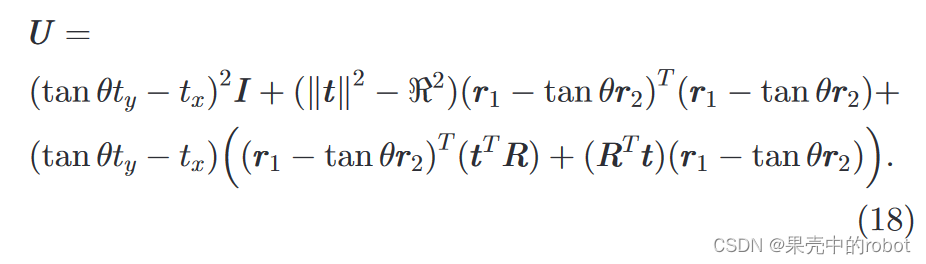
尽管光学双目系统的共轭对位于外极线上，声呐图像点 $\mathbf{s}$ 的匹配点 $\mathbf{p}$ 位于圆锥曲线 ${\mathbf{p}}^T\mathbf{U}\mathbf{p}=0$上。将方程展开为：

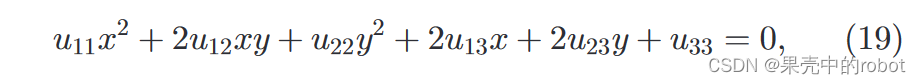
轮廓形状由代表二次项系数的上 $2\times 2$ 子块的两个特征值的符号决定（见表 1），这是由 2×2 子块的行列式决定的：

表1 基于矩阵U的上 2×2 子块部分的两个特征值符号（与二次项系数相对应）决定的外极曲线类型

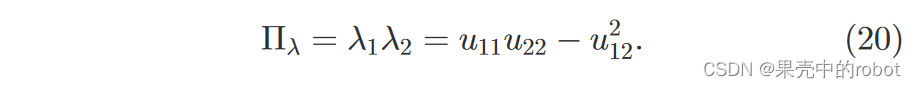
• ellipse-椭圆； circle-圆；point-点；no curve-无曲线
• parabola-抛物线；2 parallel lines-2条平行线；1 line-1条直线；no curve-无曲线
• hyperbola-双曲线；2 intersecting lines-2条相交线

3.1.1 平行相机

考虑平行相机的常用配置。在这种情况下，我们可以很容易地确定光学图像中外极曲线的几何形状。对于这种配置，我们有：

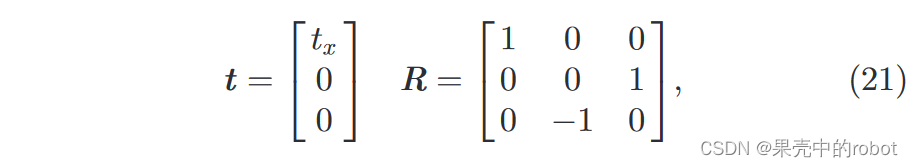
其中 $\mathbf{R}$ 表示绕 X 轴旋转90度，使声呐的 Y 轴与相机的光学 Z 轴对齐（见图1a），这与图2中假定的声呐坐标系一致，其中 Y 轴指向目标方向。

可以证明：

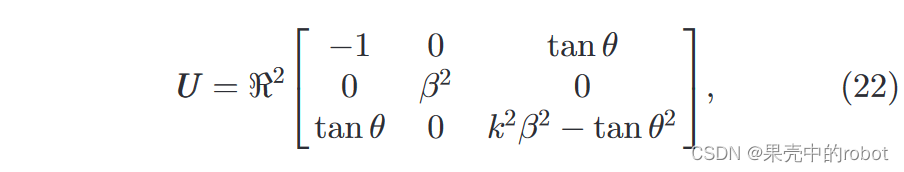
其中 $\beta =t_x/\mathfrak{R}$, $k^w=1+{\tan }^2\theta$。由此可以得出圆锥曲线的方程为双曲线（如图6a）：

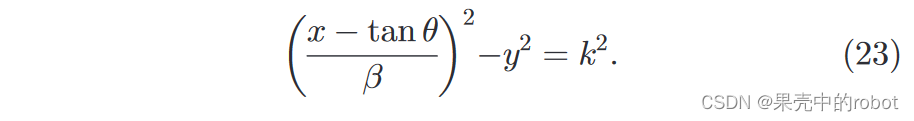
随着基线 $t_x$ 减小，即 $\beta \to 0$，外极曲线趋向垂直线：

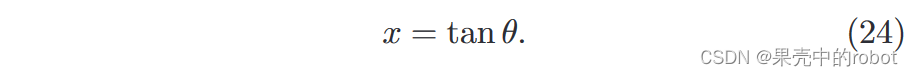
图5是 表2 Case1中的参数设置相对应的示例。

表2 计算机模拟中使用的各参数

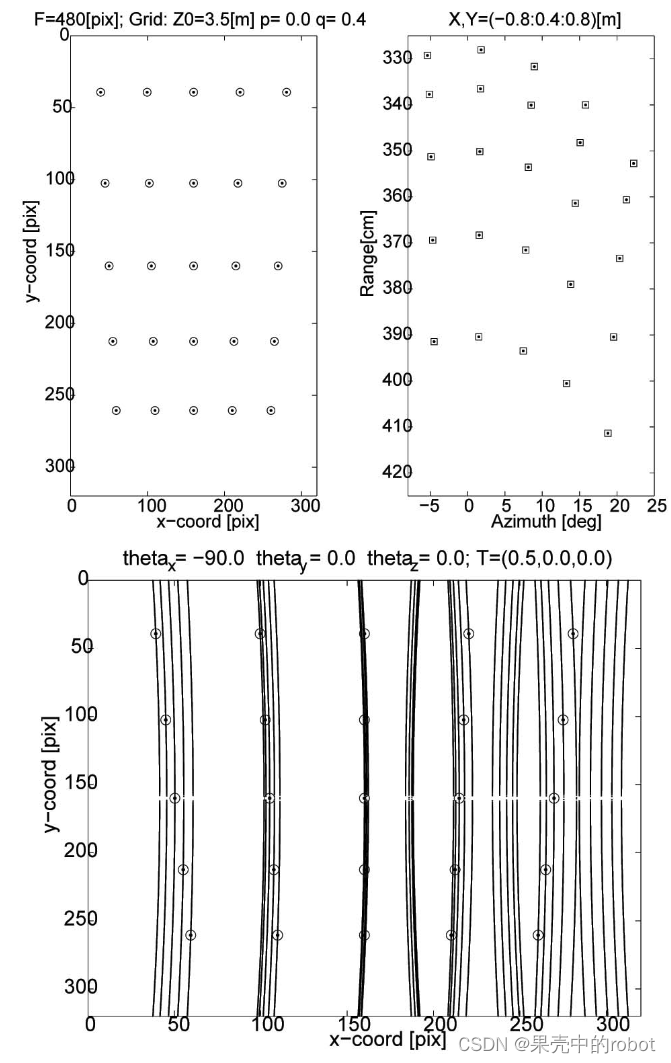
图5 （a）在平行配置相机时，光学图像中的 (由外极轮廓线组成的) 圆锥曲线为双曲线；（b）当 $\theta +{\theta }_y$ 角度较小时，形状保持不变；（c）角度较大时，形状变为椭圆。

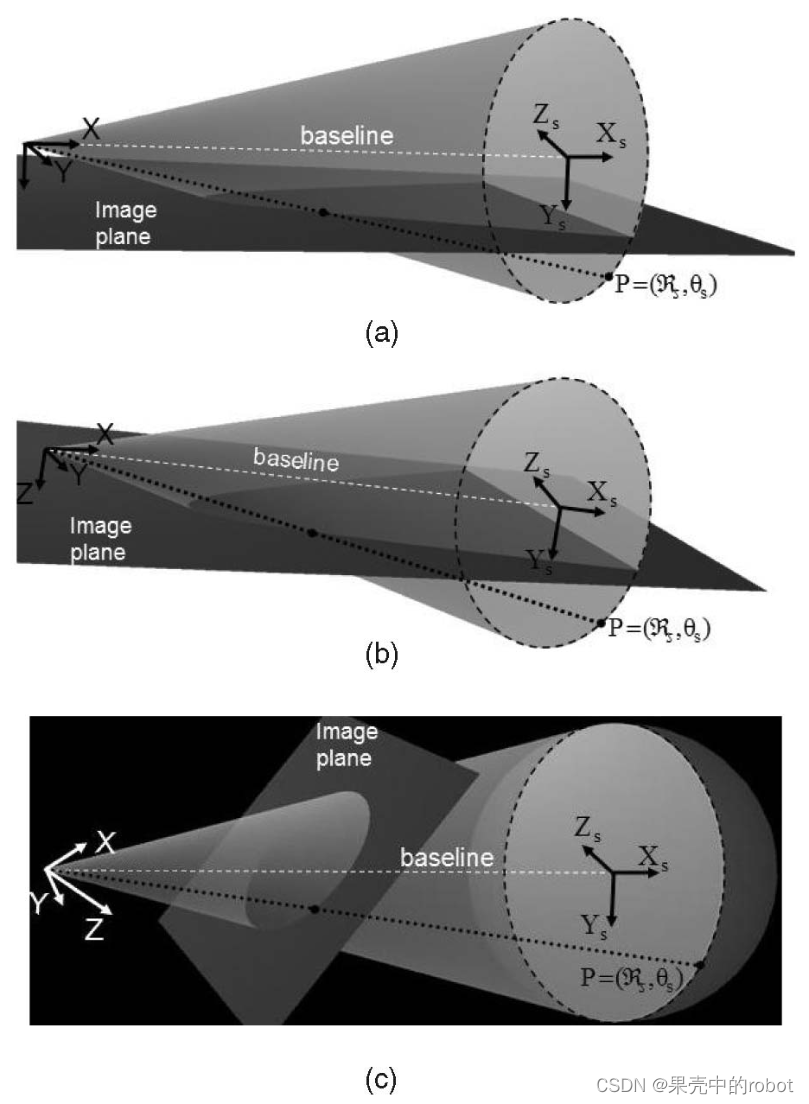
图6 利用 平行 相机合成网格的光-声双目立体图像

3.1.2 汇聚相机

同样，不失一般性地，我们假设基线与声呐 X 轴重合，相机坐标系的 $X_o$ 轴与基线方向成 ${\theta }_y$ 角。两个坐标系通过旋转矩阵 $\mathbf{R}$ 联系起来，形式如下：

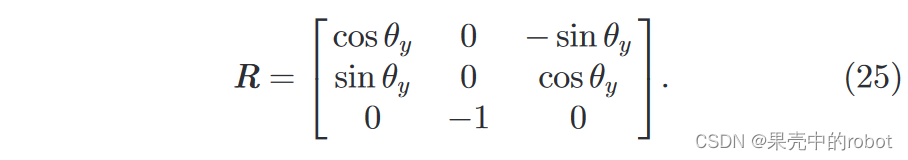
通过一些繁琐的代数，可以得出：

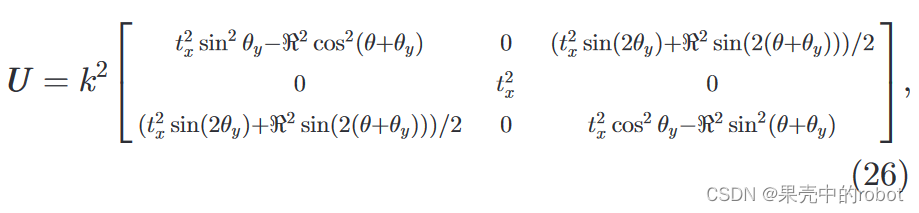
其中 $k^2=1+{\tan }^2\theta$，与前面一致。我们注意到，上 2×2 部分是一个对角矩阵，因此特征值为 ${\lambda }_1=k^2{t}_x^2>0$ 且 ${\lambda }_2=k^2(t_x^2{\sin }^2{\theta }_y-{\mathfrak{R}}^2{\cos }^2(\theta +{\theta }_y))$。根据 ${\lambda }_2$ 的符号，外极曲线可分别变为椭圆或双曲线，这取决于双目立体位姿参数 $t_x$ 和 ${\theta }_y$，以及声呐点的坐标 { R , θ } \{\mathfrak{R}, \theta\} {R,θ}。图1c 是“大致典型”的汇聚配置的俯视图，我们可以利用各种参数之间的关系来约束 ${\lambda }_2$。特别是，对“收敛点” { R 0 , 0 } \{\mathfrak{R}_0, 0\} {R0​,0} 的评估显示了平均行为：

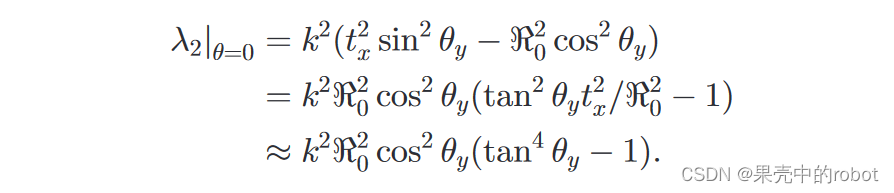
这表明两个特征值对于小的“汇聚角”保持相反的符号 ${\theta }_y$（目前缺乏更好的术语，暂称为汇聚角），如图6b所示。毫不奇怪，外极曲线仍然是双曲线，就像在平行相机配置的情况下一样。对于足够大的汇聚角，例如 ${\theta }_y\approx \pi /4$或更大，外极曲线呈椭圆状（如图6c所示）。

图7展示了在目标位置、方向、相机参数和基线（表 2 中的情况 2-4）相同的情况下改变 ${\theta }_y$ 的示例。如图7a所示，平行配置相机的外极坐标曲线为双曲线。在 ${\theta }_y\le 30$ 度时，它们仍然是双曲线，如图7b所示。然而，当汇聚角 ${\theta }_y$ 足够大，达到60度时，它们就会变成椭圆，如图7c所示，用粗虚线表示。

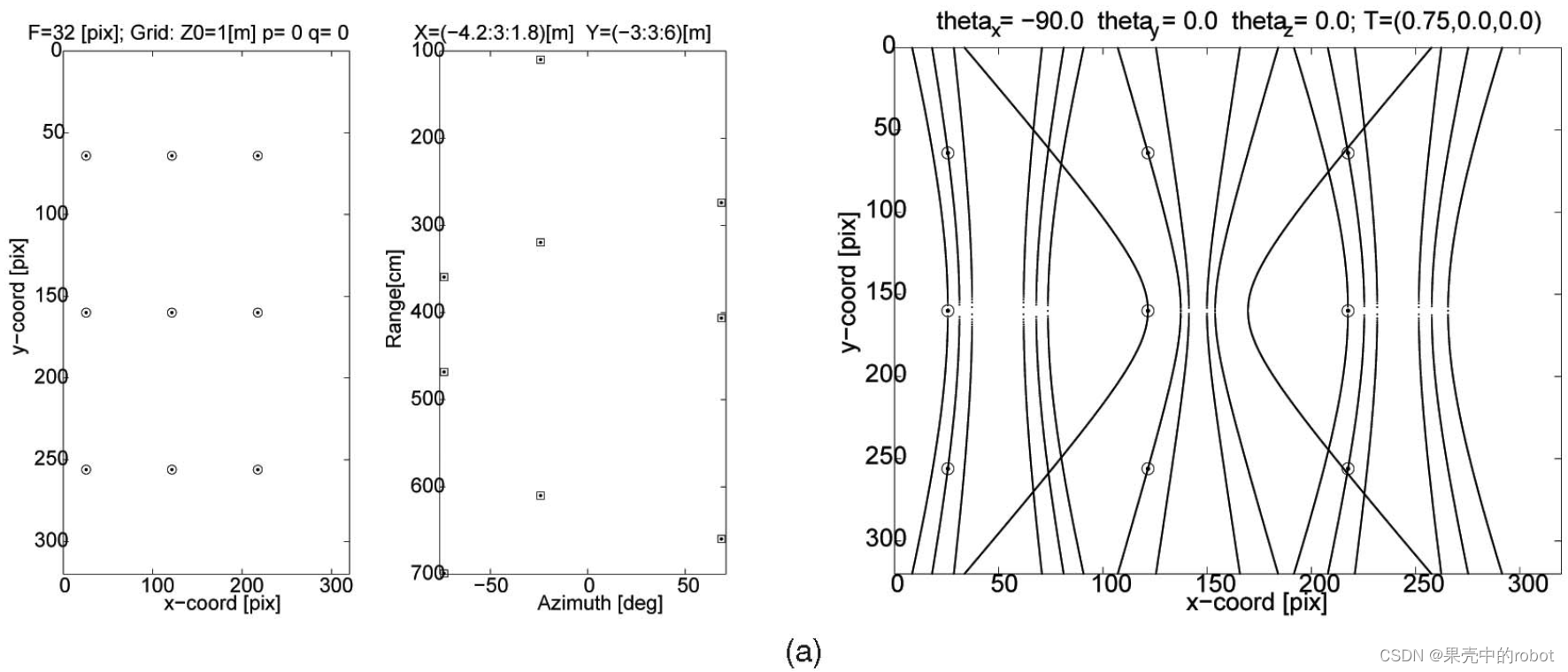
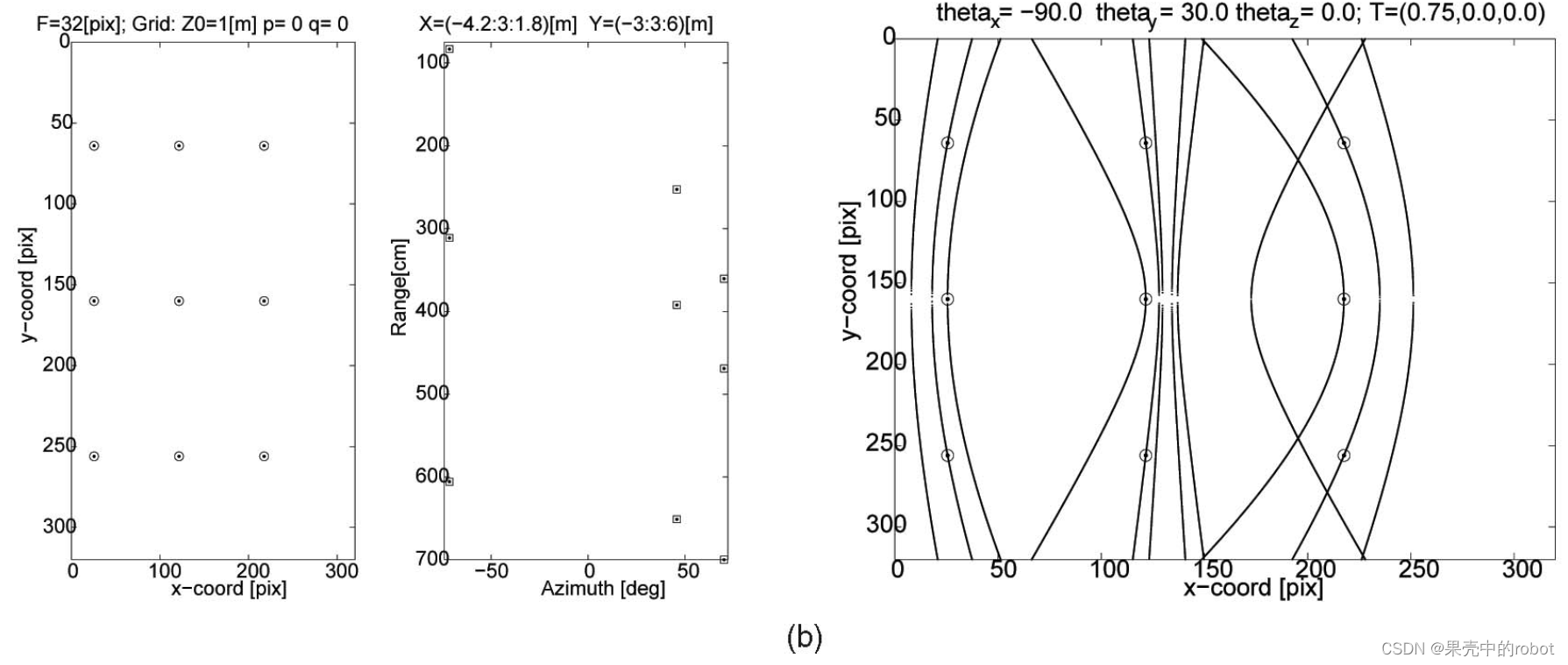
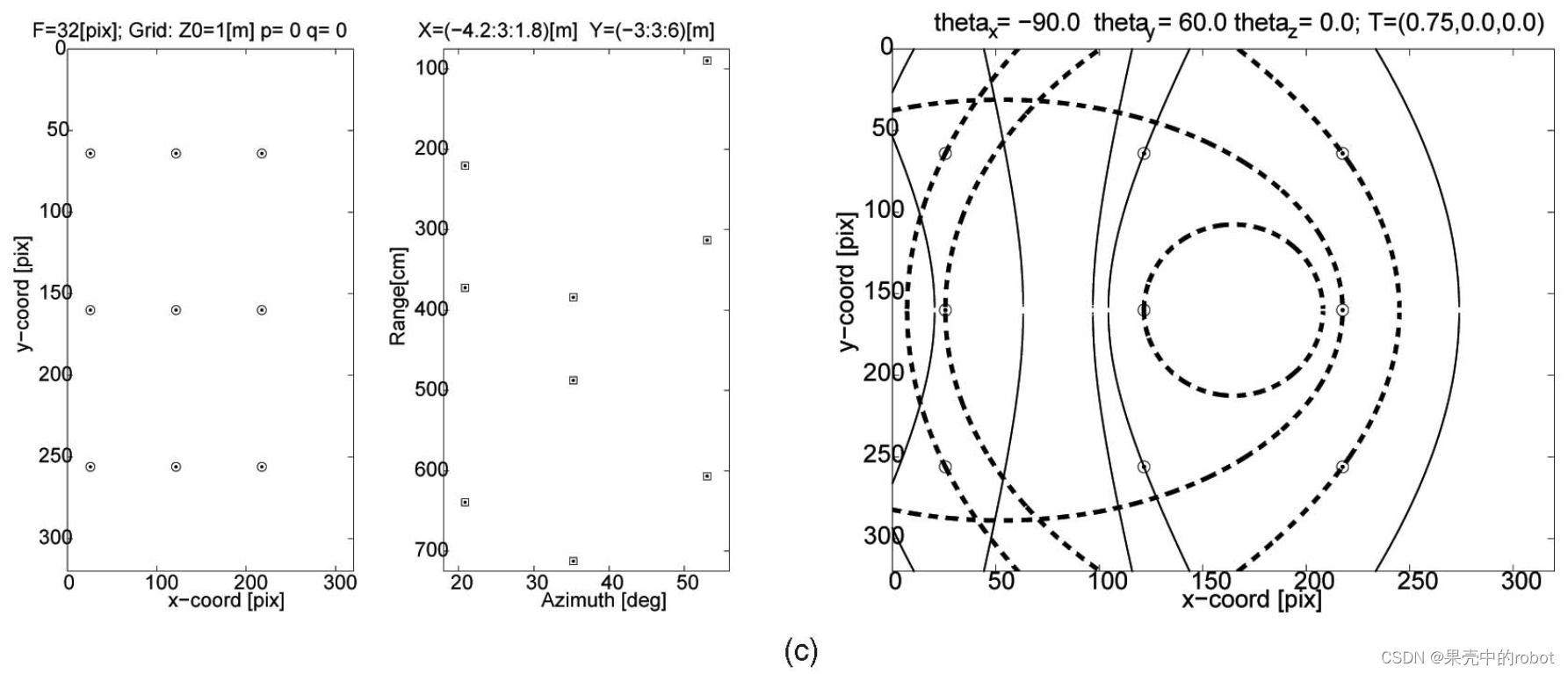
图7 对于相同网格的几何形状和距离，汇聚 相机的汇聚角不同时的光声双目图像。外极曲线（a）在 平行 相机中为双曲线，（b）在较小的汇聚角下仍为双曲线，但在较大的汇聚角下会变为椭圆，如（c）中虚线所示。

3.1.3 任意配置的相机

为了完整性，我们给出了一般立体相机配置的相同结果。在这种情况下，两个特征值的乘积为：

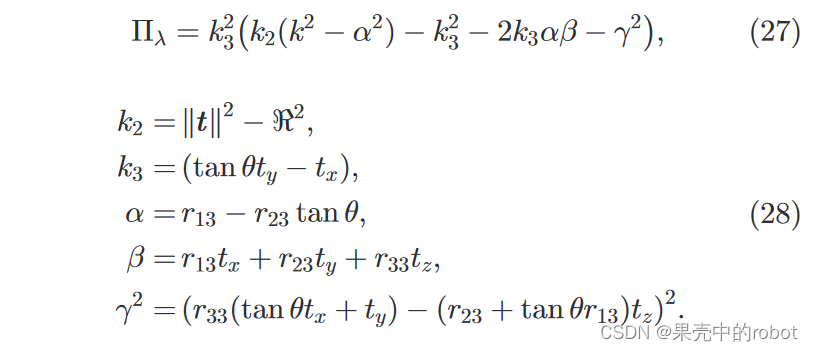
在不失一般性的前提下，假设基线与 X 轴对齐，则简化为

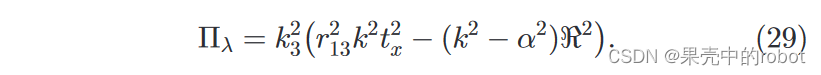
对于汇聚相机的配置，在 { R 0 , 0 } \{\mathfrak{R}_0, 0\} {R0​,0} 处求得的平均值大致为：

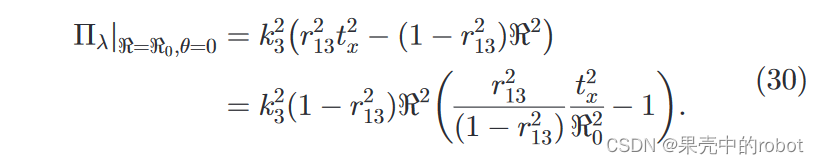
外极轮廓在图像上的分布大致可分为以下几类：

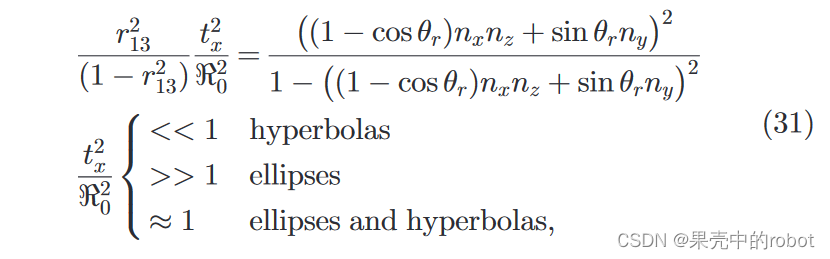
其中 ${\theta }_r$ 和 $\mathbf{n}=(n_x,n_y,n_z)$ 由旋转矩阵 $\mathbf{R}$ 分解得到的旋转角度和旋转轴确定的（根据 Rodriguez formula 罗德里格斯公式）。基于此，我们可以很容易地验证轮廓在以下几种情况下仍然是双曲线：

1. 相对于目标距离，基线较小（$t_x/\mathfrak{R}<1$）;
2. $\mathbf{n}$ 几乎平行于 $X_s$ 轴，${\theta }_r\approx \pi /2$（即基本平行的相机）。

3.2 光学相机到声呐的映射

现在我们考虑反向的映射：我们给定了 $P$ 点的光学图像投影点 $\mathbf{p}=(x,y,1)$，并希望在声呐图像中确定匹配点 $\mathbf{s}=(\mathfrak{R},\theta )$ 的位置/轨迹。

我们从（7）开始，写成如下形式：

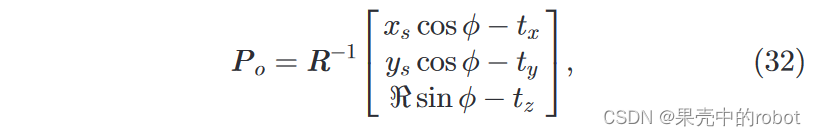
其中 $x_s=\mathfrak{R}\sin \theta$， $y_s=\mathfrak{R}\cos \theta$ 表示声呐像素在直角坐标系中的位置。通过跳过繁琐的代数，包括 1）利用光学相机的投影方程，2）求解 $\sin \varphi$ 和 $\cos \varphi$，以及 3）利用三角恒等式 ${\sin }^2\varphi +{\cos }^2\varphi =1$，我们最终得出：

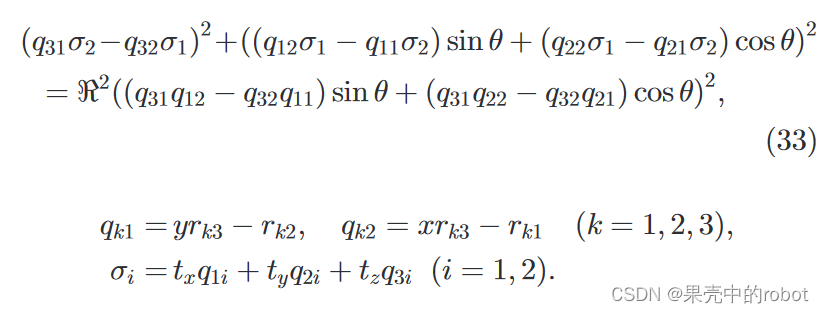
这就给出了匹配声呐像素的距离和方位角坐标之间的约束条件：

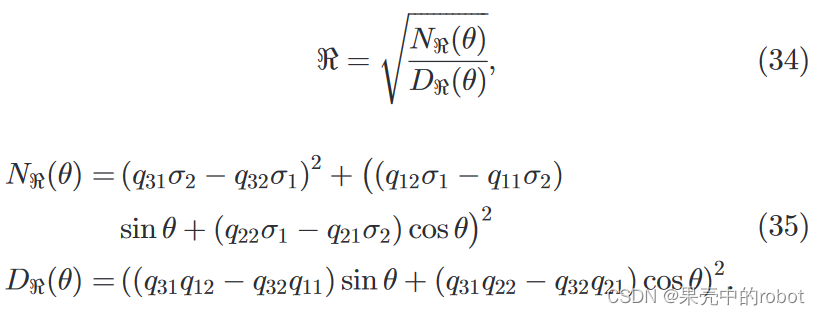
它可以用简洁的形式表示为：

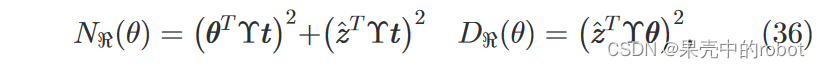
其中 $\hat{z}=(0,0,1{)}^T,\mathbf{\theta }=(\sin \theta ,\cos \theta )$，以及 ${\rm Y}$ 是一个以 $\mathbf{v}=\mathbf{R}\mathbf{p}$ 的分量定义的 3×3 斜对称矩阵（对于任意向量 $\mathbf{x}$，都有 ${\rm Y}\mathbf{x}=\mathbf{v}\times \mathbf{x}$）：

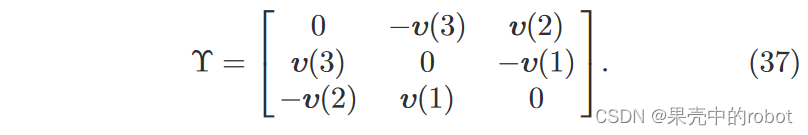
3.2.1 平行相机配置

我们再次考虑平行相机的特殊配置情况。在这里，测距方程的分子和分母变为：

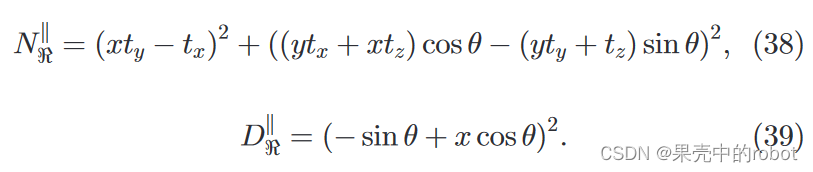
如果我们将基线与 $X_o$ 方向对齐，则可以进一步简化为

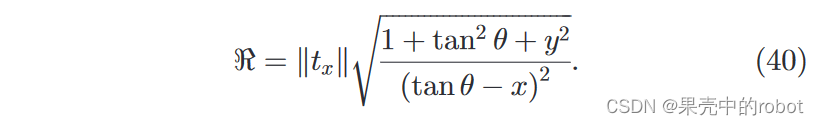
图 8 描述了基于表 2 中 Case 1 参数的一个特定示例。如图8a所示，目标点位于声呐下程视场内，大致在 3 或 4 米处。在中间和下面的行中，我们分别以对数图的形式显示了图像内的部分（假定声呐视场）以及整条外极曲线。假定的下射程视场位于对数图中两条水平实线之间。为了清晰和区分各种轮廓，方位角大致相同的点的外极曲线采用相同的线条样式（实线、虚线、虚点线和点线）。图8b中给出了一个汇聚立体相机配置，与 表2 中的 Case 2 相对应。

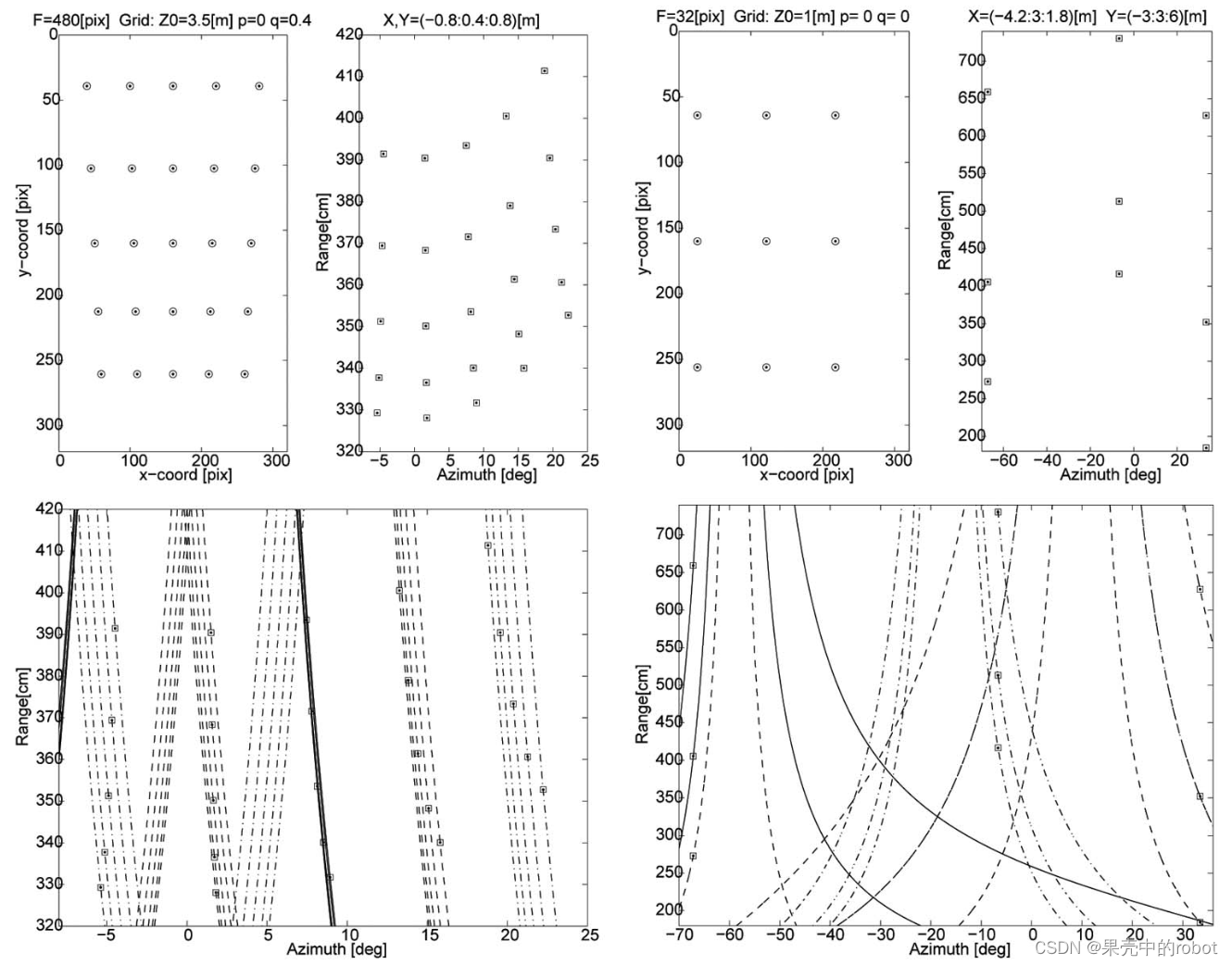
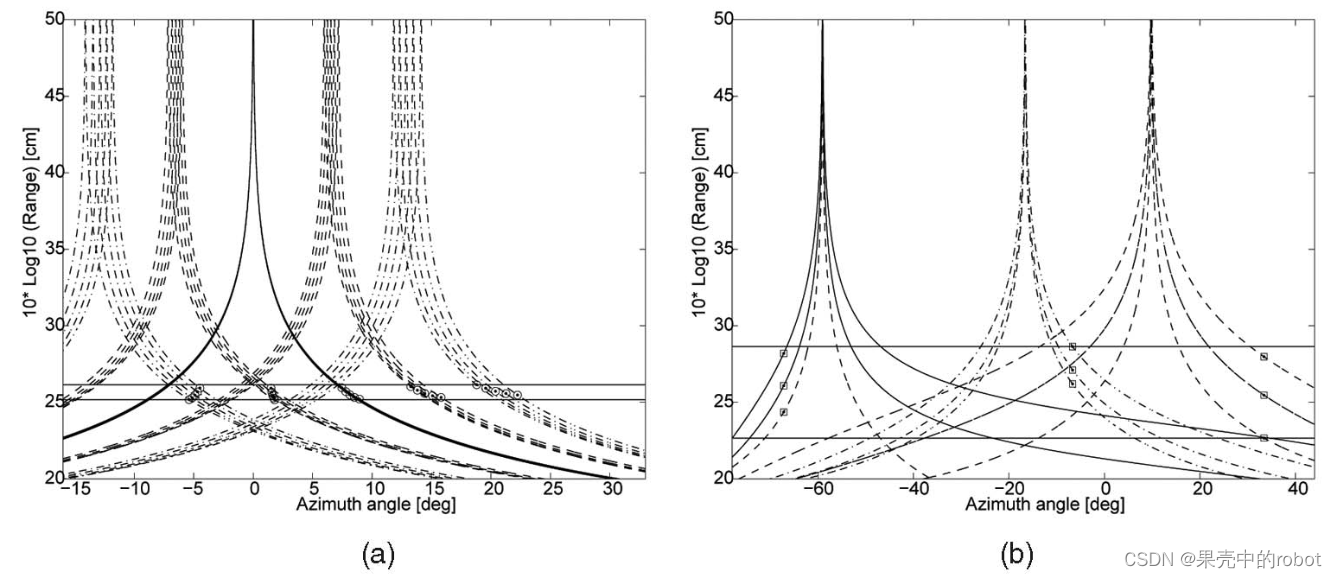
图8 两个采用（a）平行和（b）汇聚相机配置的光-声立体对示例：在假设的下射程视场范围内和以对数图形式展示的更大距离窗口内的对极几何（参数列于 表2 中的 Case1 和 Case2 下）。

回想一下，DIDSON 波束的仰角波束宽度为 $w_{\varphi }=14$；也就是说，声呐视图中成像的任何一点都是以 $-7\le \varphi \le 7$ [deg] 为边界。因此，光声立体视图中的对应点对被限制在一小段外极曲线上。这种所谓的 声学视图可见性约束 缩小了匹配特征的搜索范围。在图 9 的示例中，粗体线段描述了这些曲线的一部分，对应于仰角为 $\pm$ 7 [度] 的三维点。虚线覆盖了更大的部分，仰角为 $-15\le \varphi \le 15$ [deg]。虚线矩形大致是光学相机视场范围内的区域，在本例中假定约为 53 度。

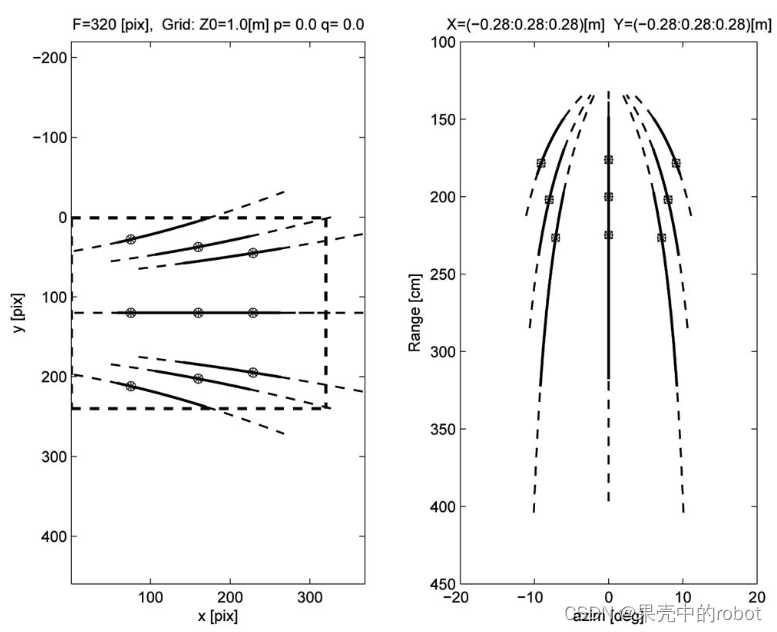
图9 对极坐标曲线，黑色部分突出显示了声呐视图中可见的声呐化场景（每个波束的 $\pm$ 7 [deg]仰角宽度内的三维点）

4. 立体三角测量

用匹配点对 { p , p ′ } \{\bm{p}, \bm{p}'\} {p,p′} 的投影射线进行三角测量是从两个光学视图重建三维目标点 $P$ 的基本原理。在理想情况下，这些光线相交于所寻找的三维点。对于有噪声的数据，可能不存在交集，可以根据 $P$ 的三个未知坐标的四个约束条件最小化适当的距离度量来计算最佳估计值 [14]。每对对应点 { p , p ′ } \{\bm{p}, \bm{p}'\} {p,p′} 的四个约束条件都是线性的，形式为 ${\mathbf{a}}^i\cdot \hat{\mathbf{P}}=0(i=1,\cdots ,4)$，由投影方程 $\hat{\mathbf{p}}=\mathbf{C}\hat{\mathbf{P}}$ 和 ${\hat{\mathbf{p}}}^{\prime }={\mathbf{C}}^{\prime }\hat{\mathbf{P}}$ 产生，其中 $\mathbf{C}$ 和 ${\mathbf{C}}^{\prime }$ 是 $3\times 4$ 的相机矩阵，而 $\hat{\mathbf{P}}=\lambda [X,Y,Z,1]$ 是三维点 $P$ 的齐次坐标。除去退化配置，四个对称齐次方程的任意三个都会产生一个闭式解：任何这样的解都是 $\mathbf{p}$ 的一条投影射线与通过对应点 ${\mathbf{p}}^{\prime }$ 的平面的交点，根据我们是利用 ${\mathbf{p}}^{\prime }$ 的 $x^{\prime }$ 还是 $y^{\prime }$ 分量的约束，可以构造两个这样的平面。通过反转 $\mathbf{p}$ 和 ${\mathbf{p}}^{\prime }$ 的交接，就会出现另外两个交叉点。总的来说，这些交叉点对应于四个约束条件中三个约束条件的所有可能子集。更一般地说，可以同时利用所有四个约束条件，从 $4\times 4$ 矩阵 $\mathbf{A}=[{\mathbf{a}}^1;{\mathbf{a}}^2;{\mathbf{a}}^3;{\mathbf{a}}^4]$ 的奇异值分解中得到 $\mathbf{AP}=0$ 的闭式解。

在光声立体视觉系统中，光学图像点上的投影 $\mathbf{p}=(x_o,y_o)$ 和声呐图像中匹配点的距离-方位角测量 s = { R s , θ s } \bm{s}=\{\mathfrak{R}_s,\theta_s\} s={Rs​,θs​} 会产生四个约束条件，这种冗余为每个光声立体匹配提供了不同的三维点估计值。由于两个投影模型的性质不同，这些方程是不对称的，因此在利用四个约束条件中的三个子集时，可以推导出各种封闭形式的表达式。虽然这些解法都给出了次优估计，还需要推导出最大似然估计[24]，但对这些解的几何解释及其鲁棒性的研究，对定义合适的目标函数来计算最佳估计有直接影响。

回到（10），我们有：

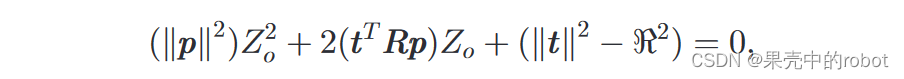
这个二次方程给出了 $Z_o$ 的两个解。在大多数情况下，目标的距离 $\mathfrak{R}$ 大于立体双目系统的基线 $t$ ，因此有 $(\Vert t{\Vert }^2-{\mathfrak{R}}^2)<0$。因此，这两个根的符号相反，并且可以识别出带有正号（$Z_o>0$）的正确解。即使有两个正解，通常也只有一个解与两台相机视场内的 3D 点相对应，或与距离测量结果一致。因此，我们可以根据 ${\mathbf{P}}_o=Z_o\mathbf{p}$ 重建三维点，例如在摄像机坐标系中的三维点。我们不难发现，这种所谓的 测距解 只需要声纳图像中的距离测量 $\mathfrak{R}$。简单的几何解释是光学相机的投影射线与 测距球面 的交点，测距球面是以声呐坐标系原点为中心的圆，半径等于三维特征的测距 $\mathfrak{R}$（见图 10a）。

图10 光声立体成像中各种三角测量方案的几何解释

等式（15）相当于仅利用方位角测量值 $\theta$ 估算出的结果：

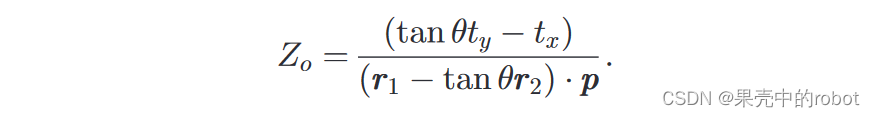
这种所谓的 方位角解 对应于光线与方位角平面的交点，该平面垂直于 $X_s{Y}_s$平面、与 $Y_s$轴成 ${\theta }_s$ 角（见图10b）。

还可以推导出其他具有明显几何解释的解法。例如，可以很容易地证明，声呐坐标系中的三维点可以用下面的形式表示：

将两个坐标系之间的变换改写为：

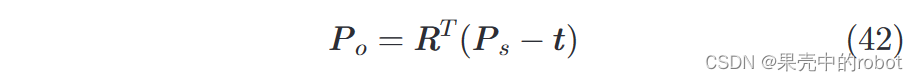
然后利用光学相机投影方程，我们可以得出：

其中 $\widetilde{{\mathbf{\alpha }}_x}=(x{\tilde{\mathbf{r}}}_3-{\tilde{\mathbf{r}}}_1),\widetilde{{\mathbf{\alpha }}_y}=(y{\tilde{\mathbf{r}}}_3-{\tilde{\mathbf{r}}}_2)$，以及 ${\tilde{\mathbf{r}}}_i(i=1,2,3)$是旋转矩阵 $\mathbf{R}$ 的列，这两个对称方程中的每一个都是非线性约束条件（回顾一下以 $Z_s$ 为参数的 ${\mathbf{P}}_s$）。每个方程都对应于大圆 { R s , θ s } \{\mathfrak{R}_s,\theta_s\} {Rs​,θs​} 与两个平面 ${\pi }_x$ 和 ${\pi }_y$ 之一的交点，这两个平面由光学中心以及通过 $\mathbf{p}=(x_o,y_o)$ 的水平和垂直扫描线之一构成（见 图10 c，其中显示了与 ${\pi }_y$ 平面交点对应的解）。

考虑利用所有四个约束条件得到的解也很有趣。可以很容易地验证，在数据完美的情况下，这相当于光学投影射线与大圆 { R s , θ s } \{\mathfrak{R}_s,\theta_s\} {Rs​,θs​} 的交点。显然，有两种可能的解，而合理的解可以通过应用“可见性约束”来确定，即位于声呐视野内的那个解。对于有噪声的数据，通常不存在交点，因此，最佳估计值可以确定为同时垂直于光学投影射线和大圆的矢量的中点。

通过对四个投影约束的操作，还可以得出其他没有明显几何解释的闭式解。例如，从上述两个方程中去掉 $Z_s$ 中的非线性项，可以得到：

其中 $\widetilde{{\mathbf{\alpha }}_{\mathbf{x}}}=({\alpha }_{x_1},{\alpha }_{x_2},{\alpha }_{x_3}),\widetilde{{\mathbf{\alpha }}_{\mathbf{y}}}=({\alpha }_{y_1},{\alpha }_{y_2},{\alpha }_{y_3})$。文献[24]和[25]提出了一种基于距离解和方位角解融合的估计，以及直接和间接非线性优化方法的最大似然估计。

5. 真实数据实验

最后，我们以平面网格的真实图像为例，验证了光声立体成像的外极几何原理，如图 11 所示。在室内游泳池设施中获得的声呐成像远远不是理想的，由于水面和混凝土池壁的反射，声呐视图被多个回波干扰。因此，在两个视图中建立匹配网格角之间的对应关系需要花费一些精力。两台相机的基线较大，约为 2.8 [m]，目标距离光学相机约 1.5 [m]。

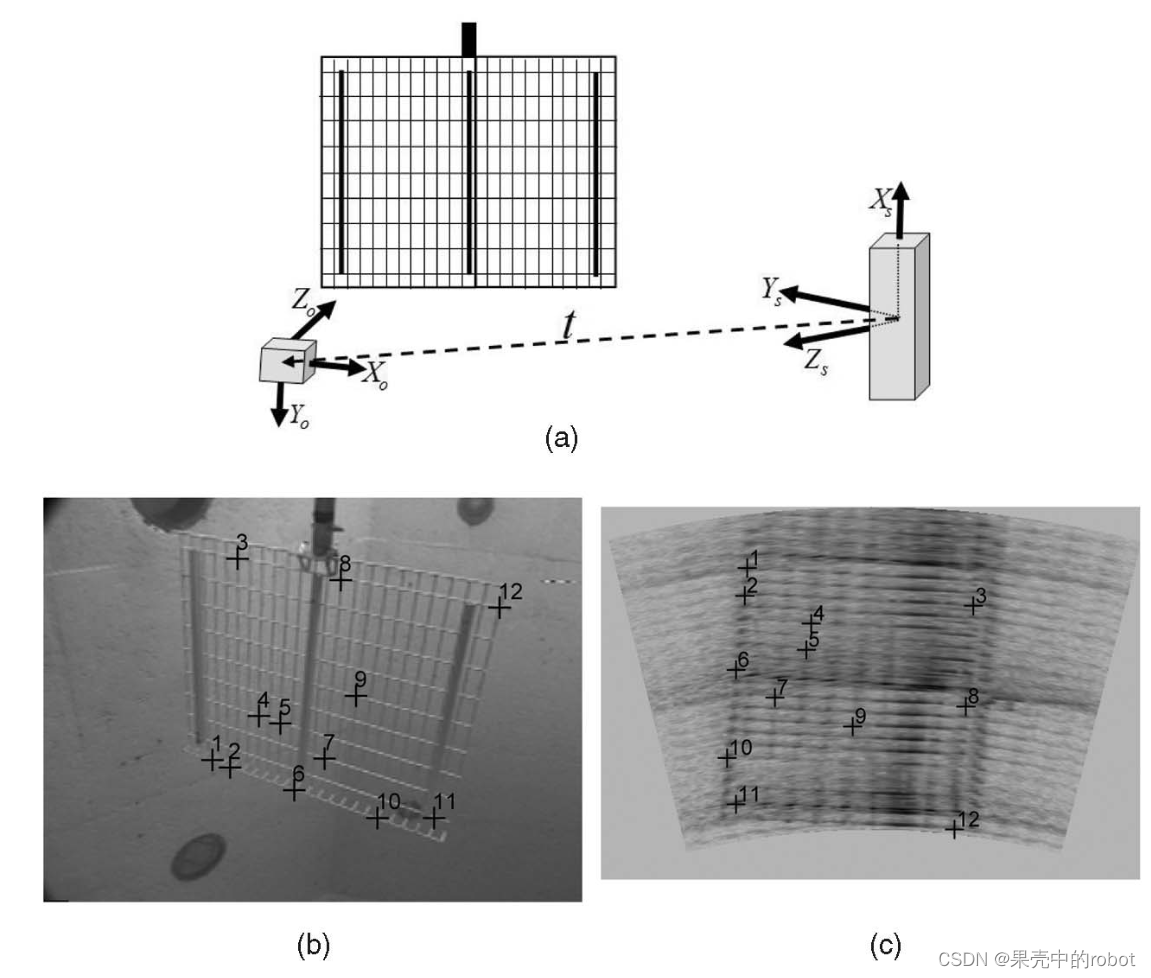
图11 （a）相对于平面网格的光-声系统配置。一个立体视图（$b,b^{\prime }$）中选定的特征映射到另一个视图($c,c^{\prime }$)中的相应外极曲线。

可以回顾一下，计算外极曲线需要知道两台相机的相对位姿（见（7）），应用[25]中的外参标定方法可以得出：

图11b 和 图11b’ 中的每对双目立体图像都标有人工选择的某些特征，根据（17）和（36）分别在图11c 和 图11c’ 中给出了相应的外极轮廓线。为增强可视性，对声呐图像进行了负化和缩放处理。根据可见性约束，声学图像中的对极线被限制在仰角 $|\varphi |\le 7$ 度的那些点上，并且可以很容易地识别极点。

6. 结束语

水下成像系统的性能直接取决于环境条件。水下能见度会随着浑浊度的增加而降低，光学成像的主要优势–高分辨率和对比度–往往会迅速减弱，这直接影响到水下光学图像特征的探测/定位精度。相比之下，声呐图像在浊度变化方面更鲁棒，尽管对各种声学噪声源更敏感。因此，虽然在清澈水域中光学图像的特征定位相对精度较高，但随着浊度的增加，声学图像特征定位的相对精度自然也会提高。因此，在评估光学声学立体成像系统的优点时，有两个值得注意的问题：1) 在不同的水浊度条件下，重建精度与传统双目系统相比如何？2) 是否存在与浊度水平无关的固有优势？人们可能会直观地认为，光声立体系统将提供更高的精度，仅仅是因为声学相机的距离测量约束了立体三角测量的解(见图12)。除了选定的直接和间接三维重建方法外，文献[24]和[25]还根据一系列浊度条件下的误差分析和计算机模拟，对光声立体成像系统与传统双目系统的性能进行了深入研究。结果表明，尽管两种立体系统在低浊度条件下具有相当的近距离成像性能，但在目标距离较大和能见度较低的条件下，光声系统的性能要优于传统系统。例如，众所周知，在传统双目系统中，对于相同的测量噪声水平，估计精度随着基线的增加而提高，而随着目标距离的增加而下降。虽然方位角解具有相同的特性和缺点，但距离解在更大的目标距离范围内保持大致相同的精度 [24]。因此，可以根据双目立体基线和目标距离（由声学相机直接测量得到）对两种解进行最佳融合 [25]。

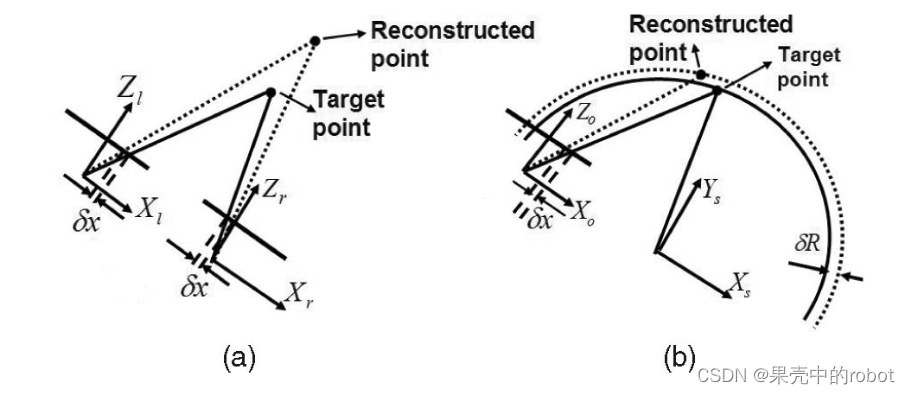
图12 在（a）传统光学双目系统和（b）光-声双目立体系统中，由于图像投影位置不准确而造成的重建误差的几何解释。

7. 总结

在一系列水下应用中，部署具有成像传感器的潜水平台变得越来越重要。传统上，光学摄像机是操作员遥控的标准设备。然而，在浑浊的水域中部署声呐摄像机是不可避免的，例如，对水下港口结构进行目视检查。与传统的立体系统一样，光声立体成像中的双目线索也可以利用重叠视图进行排列，根据对应点或区域的匹配进行三维重建。我们推导出了外极几何和立体三角测量的支配方程，并选择了具有特定几何解释的闭式解，这些解在最大似然三维重建算法的开发中发挥了重要作用。目前正在研究的对应问题(correspondence problem)是有效部署所提出系统的一系列问题的核心。