题目链接
问题描述
答案提交
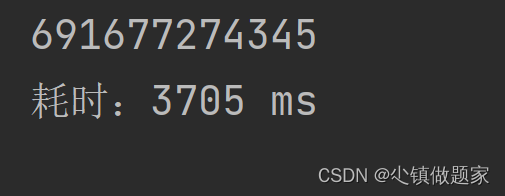
本题答案:691677274345。
思路分析
问题描述
将 3 分解成两个正整数的和, 有两种分解方法, 分别是3=1+2 和 3=2+1 。注意顺序不同算不同的方法。
将 5 分解成三个正整数的和, 有 6 种分解方法, 它们是
1+1+3 = 1+2+2 = 1+3+1 = 2+1+2 = 2+2+1 = 3+1+1。
请问, 将 2021 分解成五个正整数的和, 有多少种分解方法?
答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
本题答案:691677274345。
思路分析
填空题,所以我们只要得出答案就行,直接暴力模拟。
我们可以将公式看成一个个格子,如: 口 + 口 + 口 + 口 + 口 = 2021。
如果我们直接5个嵌套for,肯定超时,所以我们需要做一下分类,尽量不要嵌套那么多层。
那么我们就将五个格子分成两份,一份是:口+口+口 < 2021,另一份根据第一份得出来的值在继续模拟。
就变成了 (口+口+口)+口+口 = 2021。对于括号里面的三个口,我们可以开一个数组,用下标代表对应的值,比如(1+2+3) 就是array[6] ,然后让对应位置的值+1。
就是使用hash法,用数组记录括号里的值和可以得到该值的方案数,也就是key-对应值,value-对应该值的方案数,我们用数组来记录。
简单来说,我们需要一个数组,下标代表括号里面的值,该下标处的值代表能够得到这个值的方案数,比如 array[4] ,他可以是1+1+2,也就是是1+2+1,也可以是2+1+1等等,我们就假设4这个下标(括号内的值),的方案数是3,我们之后匹配剩余的两个括号的时候,就变成了 (4)+ 口 +口 = 2021,然后4这个值有3种方案得到,然后当前的两个空格也算是一种方案,所以当前这条式子的方案数是3*1 = 3。
所以当 (4) + 口 + 口 =2021的时候,我们直接把 array[4]的方案数添加到我们的记录变量中,因为值很大,需要用long long 或者 大数运算。
至于剩余的两个口,就需要我们用双层for嵌套来跑相应的值了哦。
代码如下,跑了3.8s,但是填空题嘛,出答案就算成功~
import java.math.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
//结果很大,只能用大数
BigInteger res = new BigInteger("0");
//开hash表记录三个整数和的方案数量
int[] hash = new int[2021];
//记录程序开始时间
long startTime = System.currentTimeMillis();
//先统计前面三个整数的和
for(int i = 1;i<2021;i++) {
for(int j = 1;j<2021;j++) {
for(int k = 1;k<2021;k++){
if(i+j+k < 2021) hash[i+j+k]++;
}
}
}
//再统计后面两个整数的和
for(int i = 1;i<2021;i++) {
for(int j = 1;j<2021;j++) {
if(i+j < 2021) res = res.add( new BigInteger(hash[2021-i-j]+"") );
}
}
//记录程序结束时间
long endTime = System.currentTimeMillis();
//打印结果
System.out.println(res.toString());
//打印程序运行时间
System.out.println("耗时:"+(endTime-startTime)+" ms");
}
}运行结果: