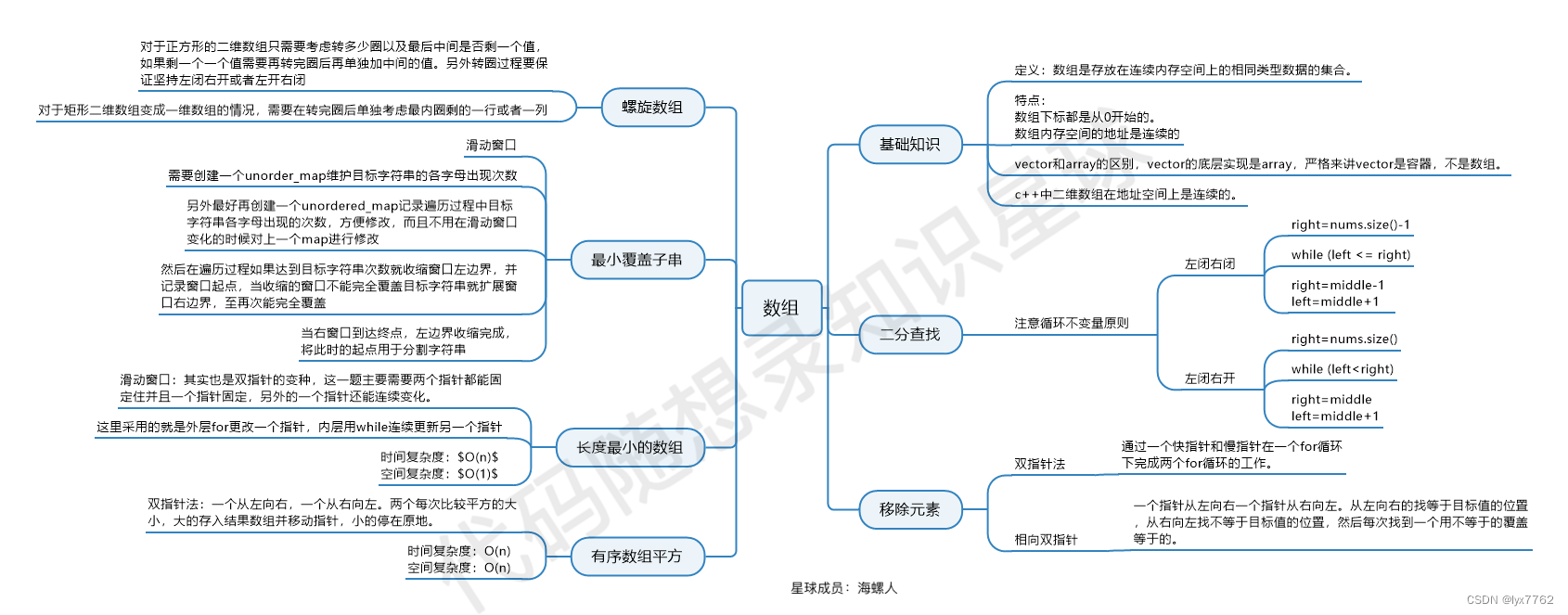
LeetCode数组相关题目整理
1. LeetCode704 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
解题思路:这道题就是典型的二分查找求解。关于二分查找以及对应的变种,查看我之前写的https://blog.csdn.net/lyx7762/article/details/128694594
/**
* 搜索区间是左闭右闭的情况
* @param nums
* @param target
* @return
*/
public int search(int[] nums, int target) {
if (nums == null || nums.length == 0)
return -1;
// 这里使用的是左闭右闭区间
int left = 0, right = nums.length - 1;
// 对于左闭右闭区间 因为left == right 也是合法的,因此需要<=
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target) {
// mid已经不满足条件,需要排出掉
// 为什么要-1 而不是right = mid
// 如果right=mid,那么实际上下一次的搜索区间为[left, mid]
// 下一次搜索区间依然包含mid,而实际上mid已经不满足要求了
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
}
2. LeetCode27 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
数组的元素是不能删的,只能覆盖。
这个题需要注意的在数组中元素的删除实际上是通过覆盖来完成的
比如[1,2,3,4,5] 现在删除数组中4的元素,那么实际上是将4后面的元素都向前移动一个单位,把4覆盖掉,的到[1,2,3,5,5],返回的数组长度-1
解题思路1(暴力法):使用两个for循环。第一个循环用来循环遍历整个数组,第二个用来移动元素。
public int removeElement(int[] nums, int val) {
if (nums == null || nums.length == 0)
return 0;
int size = nums.length;
for (int i = 0; i < size; i++) {
if (nums[i] != val)
continue;
for (int j = i; j < size - 1; j++) {
nums[j] = nums[j + 1];
}
size--;
i--; // 这个需要特别注意,因为我们覆盖元素,实际上就是将后面的元素都向前移动一位,那么i也要向前移动,否则会漏掉一些元素
}
return size;
}
解题思路2(利用快慢指针):首先需要明确快慢指针代表什么意思:
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组。
- 慢指针:指向更新新数组下标的位置
快指针从头开始遍历数组,只要发现不等于给定val的元素,就将元素赋值为slow指针指向的位置。这样循环结束后,所有的不等于val的元素都保存起来
public int removeElement(int[] nums, int val) {
if (nums == null || nums.length == 0)
return 0;
int fast = 0, slow = 0;
for (fast = 0; fast < nums.length; fast++) {
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
3. LeetCode997 有序数组平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1: 输入:nums = [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2: 输入:nums = [-7,-3,2,3,11] 输出:[4,9,9,49,121]
解题思路1:采用暴力法。直接循环遍历整个数组,求出平方。然后调用数组排序函数即可。
public int[] sortedSquares(int[] nums) {
if (nums == null || nums.length == 0)
return null;
for (int i = 0; i < nums.length; i++) {
nums[i] *= nums[i];
}
Arrays.sort(nums);
return nums;
}
解题思路2:利用双指针。因为数组本身是有序的,我们平方完以后,出现顺序不一样的原因只要是因为一些负数平方后可能大于本来的正数。根据分析可以发现,平方后数组最大的数字之可能出现在输入数组的左边或者右边(左边为最小的负数,那么平方后应该变的很大;右边为最大的正数,平方也可能很大)。
因此可以使用两个指针i, j,分别指向数组最左边和最右边的元素。另外创建一个和输入数组等大的数组
开始遍历数组,判断i, j指向的元素哪个平方最大,就保存到新数组的最后一个元素。依次类推,直到i>j位置
public int[] sortedSquares(int[] nums) {
if (nums == null || nums.length == 0)
return null;
// 定义两个指针,分别指向数组的最左边和最右边
int i = 0, j = nums.length - 1;
// 创建结果数组
int[] res = new int[nums.length];
int k = j;
while (i <= j) {
int num1 = nums[i] * nums[i];
int num2 = nums[j] * nums[j];
if (num1 > num2) {
res[k] = num1;
k--;
i++;
} else {
res[k] = num2;
k--;
j--;
}
}
return res;
}
4. Leetcode209 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
解题思路1(暴力法):使用两层for循环,第一层for循环负责子数组的起始位置,第二个for循环负责从起始位置开始依次遍历,依次求和,找到符合满足条件的子数组就break掉。
public int minSubArrayLen(int target, int[] nums) {
if (nums == null || nums.length == 0) return 0;
int min = Integer.MAX_VALUE;
for (int i = 0; i < nums.length; i++) {
// 如果一个元素就满足条件
if (nums[i] >= target) return 1;
int sum = nums[i], count = 1;
for (int j = i + 1; j < nums.length; j++) {
sum += nums[j];
count++;
if (sum >= target) {
min = Integer.min(min, count);
break; // 如果当前起始位置已经找到符合的了,就直接break,因为再往后找的不可能符合了
}
}
}
if (min == Integer.MAX_VALUE) return 0;
return min;
}
解题思路2: 使用双指针实现的滑动窗口来解决。
- 建立两个指针left, right,初始值都指向数组的第一个元素。其中left指向子数组的起始位置,right指向子数组的终止位置。
- 使用right对数组进行循环遍历,每求出来一个元素,就进行累加,并判断是否满足条件。
- 如果满足条件,则进入第二个while,从继续搜索最小的子数组。
采用这种方式,可以减少之间采用暴力法中很多累加求和的计算。
视频讲解地址:https://www.bilibili.com/video/BV1tZ4y1q7XE/
public int minSubArrayLen(int target, int[] nums) {
if (nums == null || nums.length == 0) return 0;
int min = Integer.MAX_VALUE;
// 创建两个指针
int left = 0, right = 0;
int sum = 0;
while (right < nums.length) {
sum += nums[right];
while (sum >= target) {
min = Math.min(min, right - left + 1);
sum -= nums[left];
left++;
}
right++;
}
if (min == Integer.MAX_VALUE) return 0;
return min;
}
我画了一个图来演示:

这里需要注意
while (sum >= target)我们使用了while而不是if。因为如果使用if,考虑下面的这种情况,返回的只是符合条件的子数组长度,但是不是最小的子数组长度。
5. LeetCode59 螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
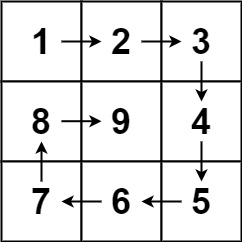
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
解题思路: 这个题首先要确定一共转几圈,然后确定每一圈的起始位置和终止位置。
转几圈:实际上转的圈数等于n/2,并且如果输入的n是奇数,那么转完n/2圈后,矩阵中心点元素还为空,因此需要手动赋值。
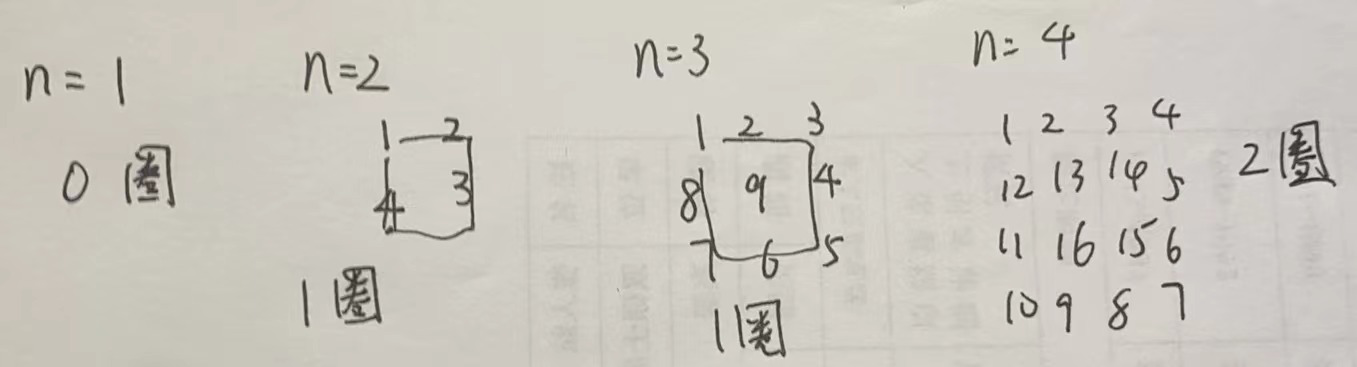
每一次处理一条边,我们都是处理的左开右闭区间,这样,对于每一条边的处理方式是统一的。
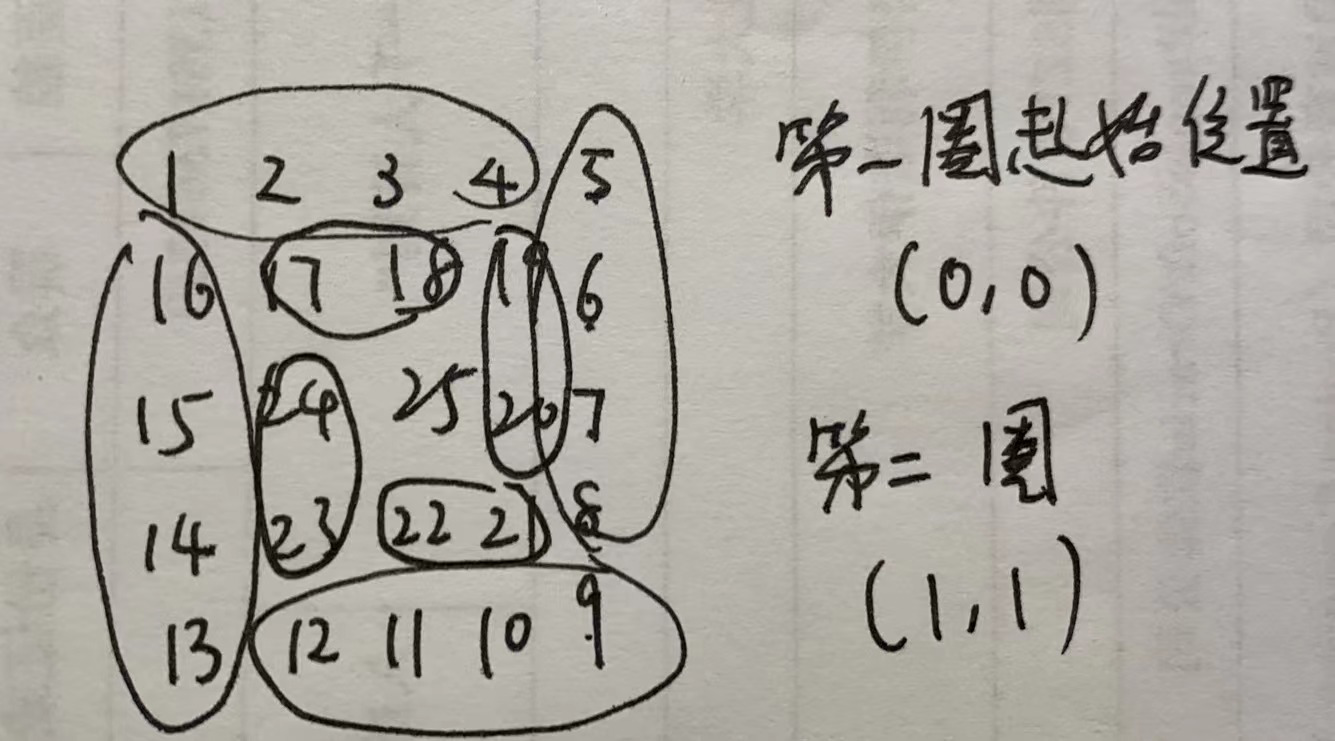
起始位置: 起始位置(0,0) (1,1)也就是起始位置每次都是上次上次起始位置+1
偏移量: 以上面的边为例,第一次遍历的区间的有边界是<n-1,第二次是n<n-2
此外,每遍历完一圈,起始位置和偏移量都需要+1
具体代码如下:
public int[][] generateMatrix(int n) {
int[][] arr = new int[n][n];
// 定义两个变量,用来记录每一圈的起始位置
int startX = 0, startY = 0;
// 定义一个计数器,用来实现给数组中元素赋值
int count = 1;
// 定义一个偏移量,因为我们处理矩阵中每一条边,都是按照左闭右开的处理方式
// 而这个偏移量就是定义最后几个元素不处理,第一圈的时候就是最后一个元素不处理
// 第二圈的时候就是最后两个元素不处理,以此类推
int offset = 1;
// 接下来就是开始循环,根据传入的n来计算需要转几圈 n / 2 = 转的圈数
// 如果n是奇数,那么最后矩阵中最中间的元素需要单独赋值为n*n
int loop = n / 2;
while (loop > 0) {
int col, row;
// 首先填充上面的边
for (col = startY; col < n - offset; col++) {
// 填充数据 行不变,变的是列
arr[startX][col] = count++;
}
// 填充右边的边
for (row = startX; row < n - offset; row++) {
// 填充数据 行变,列不变
arr[row][col] = count++;
}
// 填充下面的边
for (; col > offset - 1; col--) {
// 行不变 列变
arr[row][col] = count++;
}
// 填充左边的边
for (; row > offset - 1; row--) {
arr[row][col] = count++;
}
// 更新起始位置
startX++;
startY++;
// 更新偏移量
offset++;
// 圈数减1
loop--;
}
// 整个循环结束后,判断是否为奇数 如果为奇数,那么矩阵中中心点的值需要手动填充
if (n % 2 == 1) {
arr[n / 2][n / 2] = n * n;
}
return arr;
}