完全背包
模板:完全背包问题
问题描述
完全背包问题与01背包问题唯一的区别在于:
- 在01背包中:每个物品只有一个,要么放入背包,要么不放入背包
- 在完全背包中:每个物品有无限多个,可以不放入背包,也可以多次放入背包
解法一:二维dp
(加粗部分是和01背包中有区别的部分)
dp[i][j]:将下标小于等于 i 的物品放入容量为 j 的背包中所能取得的最大价值
在计算dp[i][j]时:对于下标为 i 的物品进行讨论:
- 如果放不下物品 i(当前背包容量小于物品 i 的体积,
j < v[i]):dp[i][j] = dp[i-1][j],即将下标小于等于 i-1 的物品放入容量为 j 的背包中所能取得的最大价值 - 如果能放下物品 i(
j >= v[i]):- 有两种选择:
- 不放入物品 i :
dp[i][j] = dp[i-1][j] - 放入物品 i :
dp[i][j] = w[i] + dp[i][j-v[i]]在本次放入物品i之前背包中可以已经有物品i了
- 不放入物品 i :
- 从二者中选择能取得的最大价值更大的一个:
dp[i][j] = max{dp[i-1][j], w[i] + dp[i][j-v[i]]}
- 有两种选择:
递推公式:
d
p
[
i
]
[
j
]
=
{
j
<
v
[
i
]
:
d
p
[
i
−
1
]
[
j
]
j
≥
v
[
i
]
:
max
(
d
p
[
i
−
1
]
[
j
]
,
w
[
i
]
+
d
p
[
i
]
[
j
−
v
[
i
]
]
)
dp[i][j] = \left\{\begin{matrix} j < v[i]: & dp[i-1][j]\\ j \ge v[i]: & \max (dp[i-1][j], w[i] + dp[i][j-v[i]]) \end{matrix}\right.
dp[i][j]={j<v[i]:j≥v[i]:dp[i−1][j]max(dp[i−1][j],w[i]+dp[i][j−v[i]])
计算顺序:
在计算dp[i][j]时可能会用到dp[i-1][j]位置和dp[i][0…j-1]位置的值,在计算dp[i][j]之前要保证这些位置的值已经计算过了。
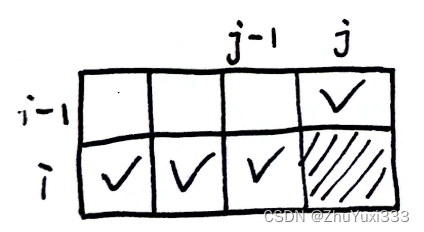
下面几种计算顺序都可以实现这一目标:
- 外循环遍历物品,内循环遍历背包容量 / 一行一行计算
- 每一行从左向右计算
- 外循环遍历背包容量,内循环遍历物品 / 一列一列计算
- 每一列从上向下计算
在计算每一行时必须按照从左向右的顺序计算,因为计算dp[i][j]时会用到本行该位置之前的数据(dp[i][0…j-1])。
但是在计算每一列时必须按照从上向下的顺序计算,因为计算dp[i][j]时会用到本行该位置之前的数据(dp[i-1][j])。
初始化:
不同的计算顺序需要初始化的内容有所不同:
- 外循环遍历物品,内循环遍历背包容量 / 一行一行计算:既需要初始化第一行,又需要初始化第一列
- 外循环遍历背包容量,内循环遍历物品 / 一列一列计算:既需要初始化第一行,又需要初始化第一列
具体来说:
- 对第一行的初始化:
i=0, j=0->V- dp[0][j]:在容量为j的背包中放物品0
j < v[0]:放不下,dp[0][j] = 0j >= v[0]:能放下,dp[0][j] = w[0]
- dp[0][j]:在容量为j的背包中放物品0
- 对第一列的初始化:
i=0->n-1, j=0dp[i][0]:在容量为0的背包中放物品,dp[i][0] = 0
public int packageComplete(){
// dp[i][j]: 将下标小于等于 i 的物品放入容量为 j 的背包中所能取得的最大价值
int[][] dp = new int[n][V+1];
// 初始化第一行: dp[0][0...j]
for(int j = 0; j <= V; j++){
// dp[0][j]:在容量为j的背包中放物品0
if(j < v[0]){
dp[0][j] = 0; // 放不下物品0
}else{
// 能放下物品0
dp[0][j] = dp[0][j-v[0]] + w[0];
}
}
// 初始化第一列:dp[0...n][0]
for(int i = 0; i < n; i++){
// 在容量为0的背包里放物品,最大价值必然为0
dp[i][0] = 0;
}
// 递推计算: 外循环遍历物品,内循环遍历背包容量
for(int i = 1; i < n; i++){
for(int j = 0; j <= V; j++){
if(j < v[i]){
// 放不下物品i
dp[i][j] = dp[i-1][j];
}else{
// 能放下物品i
dp[i][j] = Math.max(
dp[i-1][j], // 不放入物品i
w[i] + dp[i][j-v[i]] // 放入物品i(此时背包中可以已有物品i)
);
}
}
}
// 返回结果
return dp[n-1][V];
}
解法二:一维dp / 滚动数组
观察二维dp的递推公式发现:在计算dp[i][j]时会用到前一行的第j个数据,和当前行的前j-1个数据。
d
p
[
i
]
[
j
]
=
{
j
<
v
[
i
]
:
d
p
[
i
−
1
]
[
j
]
j
≥
v
[
i
]
:
max
(
d
p
[
i
−
1
]
[
j
]
,
w
[
i
]
+
d
p
[
i
]
[
j
−
v
[
i
]
]
)
dp[i][j] = \left\{\begin{matrix} j < v[i]: & dp[i-1][j]\\ j \ge v[i]: & \max (dp[i-1][j], w[i] + dp[i][j-v[i]]) \end{matrix}\right.
dp[i][j]={j<v[i]:j≥v[i]:dp[i−1][j]max(dp[i−1][j],w[i]+dp[i][j−v[i]])
如果我们按照 “一行一行计算,每一行从左往右计算” 的顺序进行二维dp的计算:
...
在计算dp[i][j-1]时会用到dp[i-1][j-1]和dp[i][0], dp[i][1]...dp[i][j-2]
在计算dp[i][j] 时会用到dp[i-1][j] 和dp[i][0], dp[i][1]...dp[i][j-2], dp[i][j-1]
在计算dp[i][j+1]时会用到dp[i-1][j+1]和dp[i][0], dp[i][1]...dp[i][j-2], dp[i][j-1], dp[i][j]
...
观察发现,在计算完dp[i][j]之后,就再也用不到dp[i-1][j]。
综上所述,我们可以只用一行(即一个长度为V+1的数组)作为dp数组,滚动存储每一行的计算结果,不再需要的数据被新计算的结果覆盖使用。
- 一开始先将该数组的内容初始化为原二维dp的第一行的内容
- 在计算原二维dp的第 i 行(
2
≤
i
<
n
2 \leq i < n
2≤i<n)时:
- 计算开始前:滚动数组中正好是原二维dp第 i-1 行的内容
- 从左向右计算(
for(int j=0; j<=V; j++)) - 递推公式修改为: d p [ j ] = { j < v [ i ] : d p [ j ] j ≥ v [ i ] : max ( d p [ j ] , w [ i ] + d p [ j − v [ i ] ] ) dp[j] = \left\{\begin{matrix} j < v[i]: & dp[j]\\ j \ge v[i]: & \max (dp[j], w[i] + dp[j-v[i]]) \end{matrix}\right. dp[j]={j<v[i]:j≥v[i]:dp[j]max(dp[j],w[i]+dp[j−v[i]])
- 由递推公式计算出的 dp[j] 实际上就是原二维dp中的 dp[i][j],而此时滚动数组中下标为 j 的位置存放的是 dp[i-1][j],这个数值在之后的计算中都用不到了,因此将其覆盖用于存储 dp[i][j]。
public int package01(){
// dp[j]: 将物品放入容量为 j 的背包中所能取得的最大价值
int[] dp = new int[V+1];
// 初始化第一行: 在容量为j的背包中放物品0
for(int j = 0; j <= V; j++){
if(j < v[0]){
dp[j] = 0; // 放不下物品0
}else{
// 能放下物品0
dp[j] = dp[j-v[0]] + w[0];
}
}
// 递推计算: 外循环遍历物品,内循环遍历背包容量
for(int i = 1; i < n; i++){
// 原二维dp中的第一列数据,每行遇到时再初始化
dp[0] = 0;
// 计算这一行的剩余数据
for(int j = 1; j <= V; j++){
// if(j < v[i]){
// // 放不下物品i
// dp[j] = d[j]; // 什么也没做
// }else{
// // 能放下物品i
// dp[j] = Math.max(
// dp[j], // 不放入物品i
// w[i] + dp[j-v[i]] // 放入物品i(此时背包中可以已有物品i)
// );
// }
if(j >= v[i]){
dp[j] = Math.max(dp[j], w[i] + dp[j-v[i]]);
}
}
}
// 返回结果
return dp[V];
}
518. 零钱兑换 Ⅱ
需要注意当总金额j = 0时,认为只有一种组合方式:什么也不选。
代码实现:二维dp
class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
// dp[i][j]: 从下标小于i的硬币面额中选择,恰好凑够总金额j的组合数
int dp[][] = new int[n][amount+1];
// 初始化第一行:只用面额为coins[0]的硬币来凑
dp[0][0] = 1; // 总金额为0时只有一种组合方式:什么也不选
for(int j = 1; j <= amount; j++) {
if(j < coins[0]){
// 总金额j小于coins[0] => 不能凑成总金额j
dp[0][j] = 0;
}else{
// 总金额j大于等于coins[0] => 如果减去当前面额后的总金额j-coins[0]不能正好凑齐,那么总金额j也无法正好凑齐;否则,先凑够j-coins[0]后再加上当前硬币面额即可,总组合数等于dp[0][j-coins[0]]
dp[0][j] = (dp[0][j-coins[0]] == 0 ? 0 : dp[0][j-coins[0]]);
}
}
// 初始化第一列:凑成总金额0 => 只有一种组合方式:什么也不选
// dp[0][0]已经在前面初始化过了
for(int i = 1; i < n; i++){
dp[i][0] = 1;
}
// 递推计算
for(int i = 1; i < n; i++){
for(int j = 1; j <= amount; j++){
if(j < coins[i]){
// 总金额j小于coins[i] => 不能选择coins[i]
dp[i][j] = dp[i-1][j];
}else{
// 总金额j大于等于coins[i] => 可以选择coins[i],也可以不选择coins[i],两种加起来为总组合数
dp[i][j] = dp[i-1][j]
+ (dp[i][j-coins[i]] == 0 ? 0 : dp[i][j-coins[i]]);
}
}
}
// 返回结果
return dp[n-1][amount];
}
}
代码实现:一维dp
class Solution {
public int change(int amount, int[] coins) {
int n = coins.length;
// dp[j]: 恰好凑够总金额j的组合数
int dp[] = new int[amount+1];
// 初始化第一行:只用面额为coins[0]的硬币来凑
dp[0] = 1; // 总金额为0时只有一种组合方式:什么也不选
for(int j = 1; j <= amount; j++) {
if(j < coins[0]){
// 总金额j小于coins[0] => 不能凑成总金额j
dp[j] = 0;
}else{
// 总金额j大于等于coins[0] => 如果减去当前面额后的总金额j-coins[0]不能正好凑齐,那么总金额j也无法正好凑齐;否则,先凑够j-coins[0]后再加上当前硬币面额即可,总组合数等于dp[j-coins[0]]
dp[j] = (dp[j-coins[0]] == 0 ? 0 : dp[j-coins[0]]);
}
}
// 递推计算
for(int i = 1; i < n; i++){
dp[0] = 1; // 初始化原二维dp中的第一列
for(int j = 1; j <= amount; j++){
// if(j < coins[i]){
// // 总金额j小于coins[i] => 不能选择coins[i]
// dp[j] = dp[j]; // 什么也没做
// }else{
// // 总金额j大于等于coins[i] => 可以选择coins[i],也可以不选择coins[i],两种加起来为总组合数
// dp[j] = dp[j] + (dp[j-coins[i]] == 0 ? 0 : dp[j-coins[i]]);
// }
if(j >= coins[i]){
dp[j] = dp[j] + (dp[j-coins[i]] == 0 ? 0 : dp[j-coins[i]]);
}
}
}
// 返回结果
return dp[amount];
}
}
377. 组合总和 Ⅳ
我觉得这道题实际上是爬楼梯的进阶版,不属于完全背包问题。
因为这道题中是要考虑选择的顺序的,(2, 1, 1)和(1, 1, 2)就是两个不同的可行解;而背包问题是不考虑顺序的,在背包问题中认为先选择1还是先选择2都是一样的,比如上一道题518. 零钱兑换 Ⅱ就是一个典型的完全背包问题。
而在爬楼梯问题中,把整个过程看作是一系列的决策过程,而在计算dp[i]时主要考虑的是:在本轮有哪几种选择?
对应到该问题中,就是:将整个过程看作是从nums数组中依次选择数字的过程,每次只能选一个数字,数字可以重复且考虑顺序,问选出的一组数字的总和正好为target的取数方式有几种?
- dp[i]:从
nums中每次选择一个数字(可以重复,考虑顺序),使得总和为i,共有几种选择 - 在计算dp[i]时:考虑在本轮有哪几种选择?(n种)
- 共n种选择,对于每一个
nums[j],(0<=j<n):如果nums[j] <= i,则可以先选出总和为i-nums[j]的一组数,然后在本轮选择nums[j] - 对所有情况求和得到本轮的总选择数
- 共n种选择,对于每一个
- 递推公式: d p [ i ] = ∑ j = 0 n − 1 { n u m s [ j ] < = i : d p [ j − d p [ i ] ] n u m s [ j ] > i : 0 } dp[i]=\sum_{j=0}^{n-1} {\begin{Bmatrix} nums[j] <= i: & dp[j-dp[i]]\\ nums[j] > i: & 0 \end{Bmatrix}} dp[i]=j=0∑n−1{nums[j]<=i:nums[j]>i:dp[j−dp[i]]0}
- 计算顺序:在计算
dp[i]时可能会用到dp[0...i-1],因此从前向后计算(i = 0 -> target)即可 - 初始化:
dp[0]的含义是 “从nums中每次选择一个数字(可以重复,考虑顺序),使得总和为0,共有几种选择”,答案是只有一种选择——什么也不选,因此dp[0] = 1;
class Solution {
public int combinationSum4(int[] nums, int target) {
int n = nums.length;
// dp[i]: 从nums中每次选择一个数字(可以重复,考虑顺序),使得总和为i,共有几种选择
int[] dp = new int[target+1];
// 初始化: 总和为0只有1种选择 => 什么也不选
dp[0] = 1;
// 递推计算
for(int i = 1; i <= target; i++){
dp[i] = 0;
for(int j = 0; j < n; j++){
dp[i] += (nums[j] <= i ? dp[i-nums[j]] : 0);
}
}
// 返回结果
return dp[target];
}
}
322. 零钱兑换
如果用-1来表示不能凑成总金额,会导致dp[]数组中元素的含义不统一,正好题目又要求要求最小值,这样的话在讨论的时候需要对-1的情况进行单独讨论,逻辑有点啰嗦。
代码实现
class Solution {
public int coinChange(int[] coins, int amount) {
int n = coins.length;
// dp[i][j]: 从下标小于i的硬币面额中选择,恰好凑够总金额j所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,则为-1 。
int[][] dp = new int[n][amount+1];
// 初始化第一行:用面额为coins[0]的硬币凑成总金额j
dp[0][0] = 0; // 总金额为0时只有一种组合方式:什么也不选,此时所需的最小硬币数为0
for(int j = 1; j <= amount; j++){
if(j < coins[0]){
// 总金额j小于coins[0] => 不能凑成总金额j
dp[0][j] = -1;
}else{
// 总金额j大于等于coins[0] => 如果减去当前面额后的总金额j-coins[0]不能正好凑齐,那么总金额j也无法正好凑齐;否则,先凑够j-coins[0]后再加上当前硬币面额即可,所需的最少硬币数等于dp[0][j-coins[0]]+1
dp[0][j] = (dp[0][j-coins[0]] == -1 ? -1 : dp[0][j-coins[0]]+1);
}
}
// 初始化第一列:凑成总金额0 => 只有一种组合方式:什么也不选,此时所需的最小硬币数为0
// dp[0][0]已经在前面初始化过了
for(int i = 1; i < n; i++){
dp[i][0] = 0;
}
// 递推计算
for(int i = 1; i < n; i++){
for(int j = 1; j <= amount; j++){
if(j < coins[i]){
// 总金额j小于coins[i] => 不能选择coins[i],问题转换为dp[i-1][j]
dp[i][j] = dp[i-1][j];
}else{
// 总金额j大于等于coins[i] => 可以选择coins[i],也可以不选择coins[i],两者取最小
// 由于-1具有特殊含义且题目要求是取最小值,此时需要进行分类讨论
if(dp[i-1][j] == -1 && dp[i][j-coins[i]] == -1){
dp[i][j] = -1; // 如果两种都不能恰好凑成
}else if(dp[i-1][j] == -1){
// dp[i-1][j] == -1, dp[i][j-coins[i]] != -1
dp[i][j] = dp[i][j-coins[i]] + 1;
}else if(dp[i][j-coins[i]] == -1){
// dp[i-1][j] != -1, dp[i][j-coins[i]] == -1
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-coins[i]] + 1);
}
}
}
}
// 返回结果
return dp[n-1][amount];
}
}
反思总结
受到前面377. 组合总和 Ⅳ的启发,我发现其实背包问题在先遍历背包容量再遍历物品的计算顺序下的一维dp优化解法就是按照 “把整个过程看作是一系列的决策过程,而在计算dp[i]时主要考虑的是在本轮如何进行决策” 的思路(这是解决动态规划问题的基本思路——多阶段决策)进行的,按照这一思路直接去思考会直观的多!因此接下来我将尝试按照这种思路来解决问题,第二轮刷题时再统一进行整理。
279. 完全平方数
该问题可以转换为完全背包问题:
- 共有 ⌊ n ⌋ \left \lfloor \sqrt{n} \right \rfloor ⌊n⌋个物品, 1 ≤ n ≤ ⌊ n ⌋ 1 \leq n \leq \left \lfloor \sqrt{n} \right \rfloor 1≤n≤⌊n⌋ ,其中第i个物品的重量为 i 2 i^2 i2
- 背包的最大容量为 n n n
- 求能使背包恰好装满的最少物品数量
思路二:多阶段决策
dp[i]: 总和为i的完全平方数的最少数量,即背包最大容量为i时使背包恰好装满的最少物品数量。
将这一过程看作一个多阶段决策过程,在每一次决策时,即计算每一个dp[i]时,从所有物品中选择一个装入背包中。
具体来说,计算dp[i]时,即背包最大容量为i时:
- 有那些选择? 背包能装下的物品下标集合为:
{
k
∣
1
≤
k
2
≤
i
}
\{ k | 1\leq k^2 \leq i \}
{k∣1≤k2≤i}
- 如果在本轮决策中选择装入物品
k,需要先在之前的决策中向背包装入重量为 i − k 2 i-k^2 i−k2 的物品。此时使得背包恰好装满时的最少物品数量等于: d p [ i ] = d p [ i − k 2 ] + 1 dp[i] = dp[i-k^2]+1 dp[i]=dp[i−k2]+1
- 如果在本轮决策中选择装入物品
- 如何做决策? 选择装入背包后,使【使得背包恰好装满时的最少物品数量】最少的那一个,其实就是对所有决策结果取最小值
class Solution {
public int numSquares(int n) {
// dp[i]: 总和为i的完全平方数的最少数量,即背包最大容量为i时使背包恰好装满的最少物品数量。
int[] dp = new int[n+1];
// 初始化
dp[0] = 0;
// 递推计算
for(int i = 1; i <= n; i++){
int min = Integer.MAX_VALUE;
for(int k = 1; k*k <= i; k++){
min = Math.min(min, dp[i-k*k] + 1);
}
dp[i] = min;
}
// 返回结果
return dp[n];
}
}
139. 单词拆分
该问题问能否用字典worddict中的单词拼出字符串s
可以转换为下面这个问题:
- 有一个字符串集合
worddict - 依次从该字符串集合中选出一系列字符串,每个字符串可以选多次(类似于有放回抽取),将这些字符串按顺序拼接
- 问能否正好拼出字符串
s
由于该问题需要考虑顺序,所以只能按照多阶段决策的思路来思考。
dp[i]:问能否用字典worddict中的单词拼出【字符串s的前i个字符组成的前缀字符串】
在每一次决策中,即在计算dp[i]时:
- 有哪些选择? 可以选择的单词的下标集合:
{
k
∣
单词
w
o
r
d
d
i
c
t
[
k
]
正好是
d
p
[
i
]
的后缀子字符串
}
\{ k | 单词worddict[k]正好是dp[i]的后缀子字符串 \}
{k∣单词worddict[k]正好是dp[i]的后缀子字符串}
- 如果在本轮决策中选择单词
worddict[k],则能否拼出字符串s取决于dp[i-worddict[k].length]
- 如果在本轮决策中选择单词
- 如何做决策?
- 如果在本轮有某一个选择能够拼出字符串
s,本轮的决策结果就为true,其实就是对所有选择的结果做或运算
- 如果在本轮有某一个选择能够拼出字符串
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
// dp[i]: 问能否用字典worddict中的单词拼出字符串s的前i个字符组成的前缀字符串
boolean[] dp = new boolean[s.length()+1];
// 初始化
dp[0] = true; // 在字典中什么都不选时,正好拼出空字符串
// 递推计算
for(int i = 1; i <= s.length(); i++){
String curStr = s.substring(0, i);
for(String word : wordDict){
dp[i] = false;
if(curStr.endsWith(word) && dp[i-word.length()]){
dp[i] = true;
break;
}
}
}
// 返回结果
return dp[s.length()];
}
}
碎碎念:事实证明直接用多阶段决策的思路做就OK!