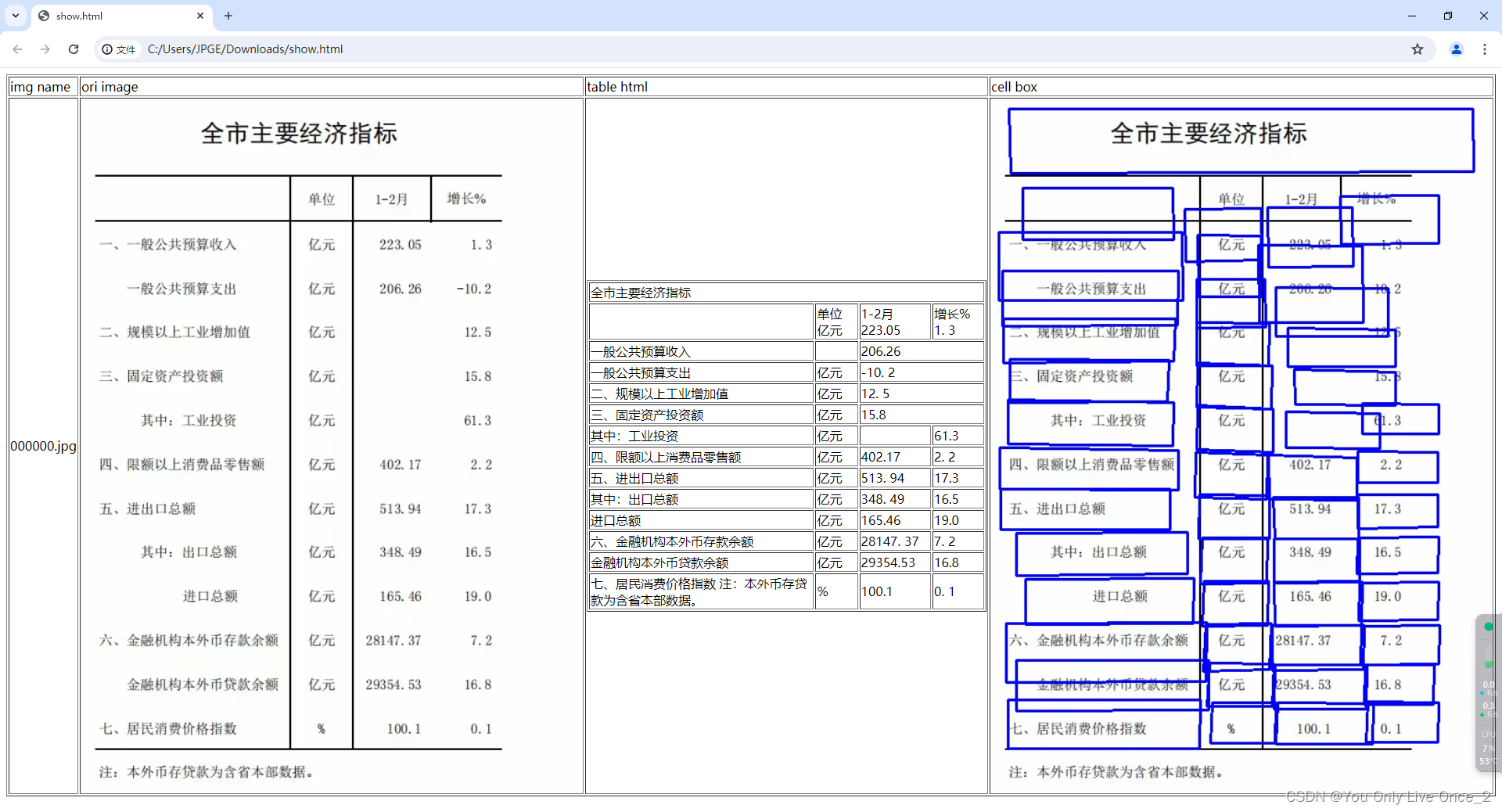
1.理论基础
题目链接/文章讲解:代码随想录
视频讲解:带你学透回溯算法(理论篇)| 回溯法精讲!_哔哩哔哩_bilibili
来自代码随想录的网站:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
所以回溯法,都可以转换成一个n叉树的树形结构,集合的大小就是子树的宽度 ,递归的深度就是树的深度。
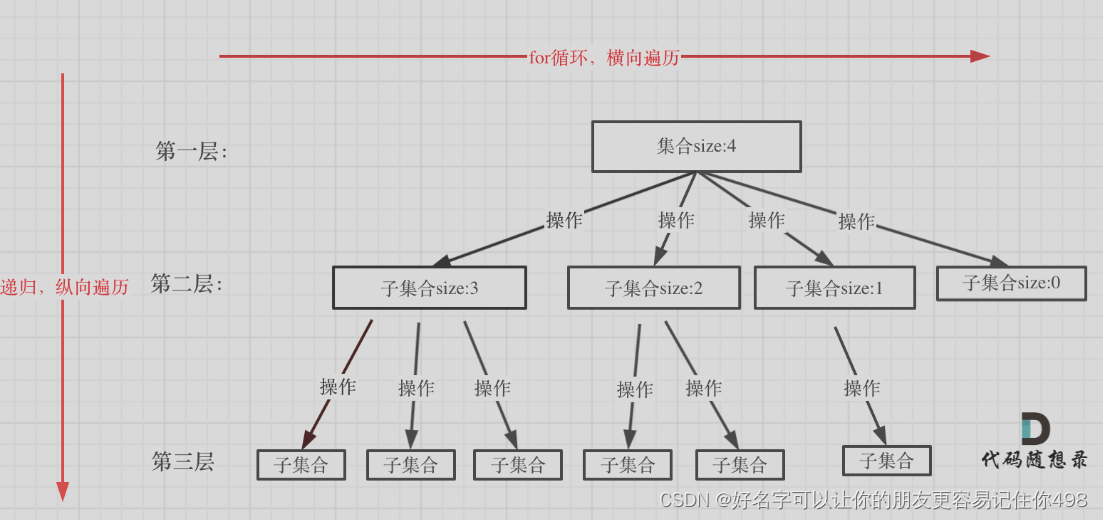
2.组合
题目链接/文章讲解: 代码随想录视频讲解:带你学透回溯算法-组合问题(对应力扣题目:77.组合)| 回溯法精讲!_哔哩哔哩_bilibili
剪枝操作:带你学透回溯算法-组合问题的剪枝操作(对应力扣题目:77.组合)| 回溯法精讲!_哔哩哔哩_bilibili
代码:(未剪枝)
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n,int k,int startIndex){
// 递归返回条件
if(path.size() == k){
result.push_back(path);
return;
}
// 遍历n叉树里的结点
for(int i = startIndex;i <= n;i++){
path.push_back(i);
backtracking(n,k,i + 1);
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
};代码:(剪枝版)
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n,int k,int startIndex){
// 递归返回条件
if(path.size() == k){
result.push_back(path);
return;
}
// 遍历n叉树里的结点
for(int i = startIndex;i <= n - (k - path.size() - 1);i++){
path.push_back(i);
backtracking(n,k,i + 1);
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
};思路:剪枝的情况就是,我们所能选择的数值的数目已经小于提上要求的组合大小,这种情况可以剪掉。
以前for循环里,i <=n ,现在,我们要求出剩余数字的数目不少于n的开始下标,即 n - (k - path.size() - 1)。这里用总数目减去已经用过的数字个数,即 k - path.size() - 1。减1,是因为我们开始时的下标为1,已经默认用了一个元素了。
其实这种套模板的题,还是很省脑的(什么?



![C++进阶 | [3] 续 | 搜索二叉树的两种模型](https://img-blog.csdnimg.cn/direct/175bc12b850543a5a5c92dc413c97f2b.png)